Non-Stationary Lipschitz Bandits

We study the problem of non-stationary Lipschitz bandits, where the number of actions is infinite and the reward function, satisfying a Lipschitz assumption, can change arbitrarily over time. We design an algorithm that adaptively tracks the recently introduced notion of significant shifts, defined by large deviations of the cumulative reward function. To detect such reward changes, our algorithm leverages a hierarchical discretization of the action space. Without requiring any prior knowledge of the non-stationarity, our algorithm achieves a minimax-optimal dynamic regret bound of $\mathcal{\widetilde{O}}(\tilde{L}^{1/3}T^{2/3})$, where $\tilde{L}$ is the number of significant shifts and $T$ the horizon. This result provides the first optimal guarantee in this setting.

Variational Bayes Portfolio Construction

Portfolio construction is the science of balancing reward and risk; it is at the core of modern finance. In this paper, we tackle the question of optimal decision-making within a Bayesian paradigm, starting from a decision-theoretic formulation. Despite the inherent intractability of the optimal decision in any interesting scenarios, we manage to rewrite it as a saddle-point problem. Leveraging the literature on variational Bayes (VB), we propose a relaxation of the original problem. This novel methodology results in an efficient algorithm that not only performs well but is also provably convergent. Furthermore, we provide theoretical results on the statistical consistency of the resulting decision with the optimal Bayesian decision. Using real data, our proposal significantly enhances the speed and scalability of portfolio selection problems. We benchmark our results against state-of-the-art algorithms, as well as a Monte Carlo algorithm targeting the optimal decision.

Prior-Dependent Allocations for Bayesian Fixed-Budget Best-Arm Identification in Structured Bandits

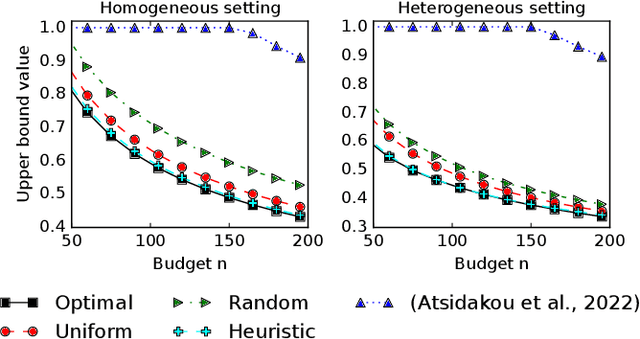
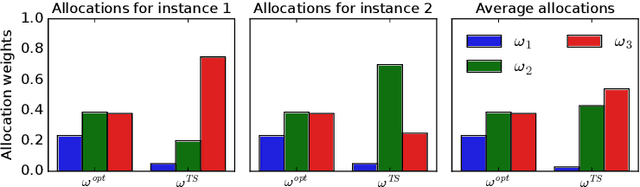
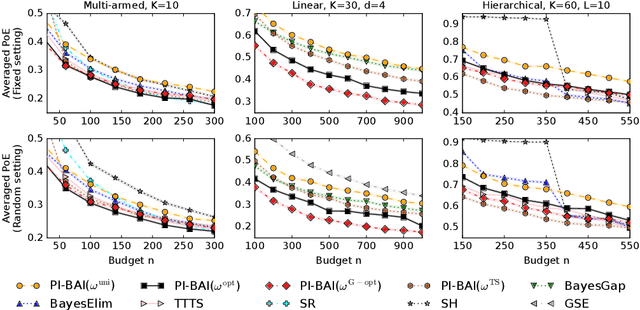
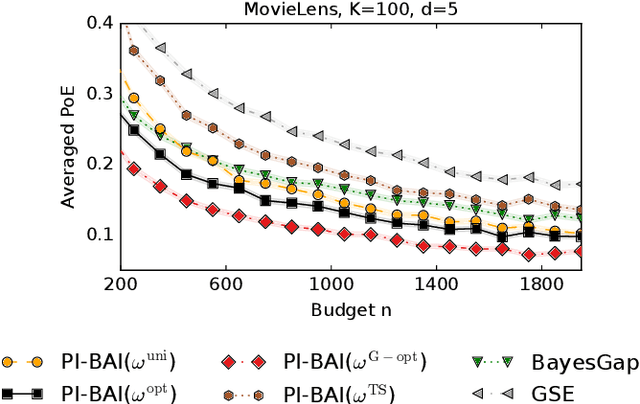
We study the problem of Bayesian fixed-budget best-arm identification (BAI) in structured bandits. We propose an algorithm that uses fixed allocations based on the prior information and the structure of the environment. We provide theoretical bounds on its performance across diverse models, including the first prior-dependent upper bounds for linear and hierarchical BAI. Our key contribution is introducing new proof methods that result in tighter bounds for multi-armed BAI compared to existing methods. We extensively compare our approach to other fixed-budget BAI methods, demonstrating its consistent and robust performance in various settings. Our work improves our understanding of Bayesian fixed-budget BAI in structured bandits and highlights the effectiveness of our approach in practical scenarios.