James Ridgway
Variational Bayes Portfolio Construction
Nov 09, 2024Abstract:Portfolio construction is the science of balancing reward and risk; it is at the core of modern finance. In this paper, we tackle the question of optimal decision-making within a Bayesian paradigm, starting from a decision-theoretic formulation. Despite the inherent intractability of the optimal decision in any interesting scenarios, we manage to rewrite it as a saddle-point problem. Leveraging the literature on variational Bayes (VB), we propose a relaxation of the original problem. This novel methodology results in an efficient algorithm that not only performs well but is also provably convergent. Furthermore, we provide theoretical results on the statistical consistency of the resulting decision with the optimal Bayesian decision. Using real data, our proposal significantly enhances the speed and scalability of portfolio selection problems. We benchmark our results against state-of-the-art algorithms, as well as a Monte Carlo algorithm targeting the optimal decision.
Concentration of tempered posteriors and of their variational approximations
Jun 07, 2018Abstract:While Bayesian methods are extremely popular in statistics and machine learning, their application to massive datasets is often challenging, when possible at all. Indeed, the classical MCMC algorithms are prohibitively slow when both the model dimension and the sample size are large. Variational Bayesian methods aim at approximating the posterior by a distribution in a tractable family. Thus, MCMC are replaced by an optimization algorithm which is orders of magnitude faster. VB methods have been applied in such computationally demanding applications as including collaborative filtering, image and video processing, NLP and text processing... However, despite very nice results in practice, the theoretical properties of these approximations are usually not known. In this paper, we propose a general approach to prove the concentration of variational approximations of fractional posteriors. We apply our theory to two examples: matrix completion, and Gaussian VB.
Probably approximate Bayesian computation: nonasymptotic convergence of ABC under misspecification
Jul 19, 2017



Abstract:Approximate Bayesian computation (ABC) is a widely used inference method in Bayesian statistics to bypass the point-wise computation of the likelihood. In this paper we develop theoretical bounds for the distance between the statistics used in ABC. We show that some versions of ABC are inherently robust to misspecification. The bounds are given in the form of oracle inequalities for a finite sample size. The dependence on the dimension of the parameter space and the number of statistics is made explicit. The results are shown to be amenable to oracle inequalities in parameter space. We apply our theoretical results to given prior distributions and data generating processes, including a non-parametric regression model. In a second part of the paper, we propose a sequential Monte Carlo (SMC) to sample from the pseudo-posterior, improving upon the state of the art samplers.
On the properties of variational approximations of Gibbs posteriors
Jun 15, 2015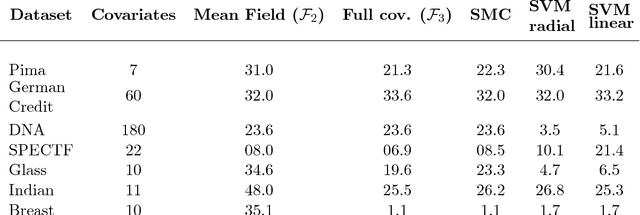
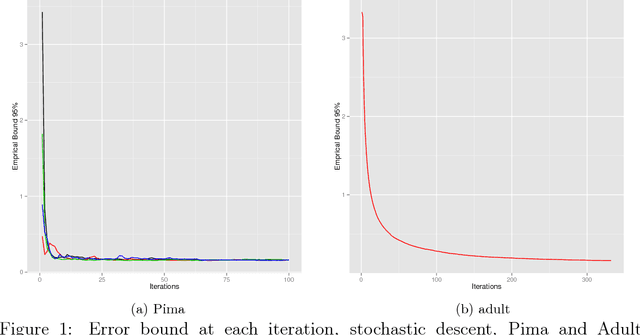

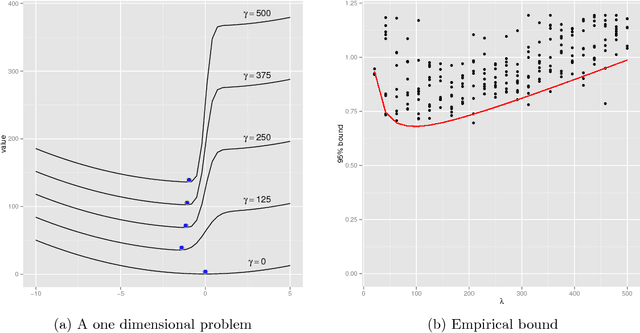
Abstract:The PAC-Bayesian approach is a powerful set of techniques to derive non- asymptotic risk bounds for random estimators. The corresponding optimal distribution of estimators, usually called the Gibbs posterior, is unfortunately intractable. One may sample from it using Markov chain Monte Carlo, but this is often too slow for big datasets. We consider instead variational approximations of the Gibbs posterior, which are fast to compute. We undertake a general study of the properties of such approximations. Our main finding is that such a variational approximation has often the same rate of convergence as the original PAC-Bayesian procedure it approximates. We specialise our results to several learning tasks (classification, ranking, matrix completion),discuss how to implement a variational approximation in each case, and illustrate the good properties of said approximation on real datasets.
PAC-Bayesian AUC classification and scoring
Oct 13, 2014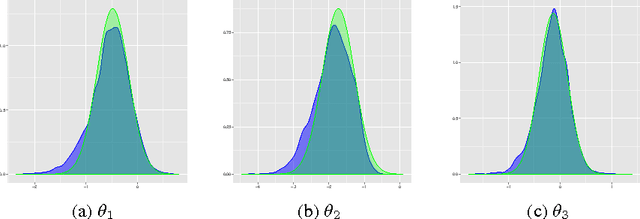
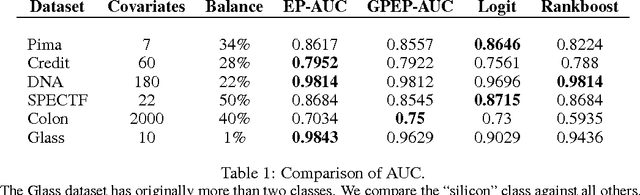
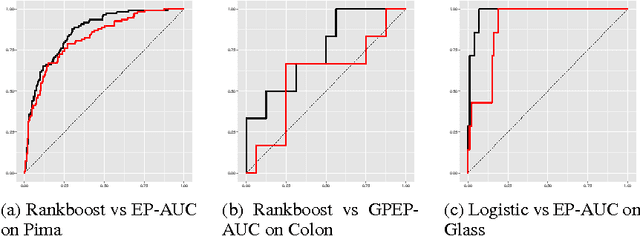

Abstract:We develop a scoring and classification procedure based on the PAC-Bayesian approach and the AUC (Area Under Curve) criterion. We focus initially on the class of linear score functions. We derive PAC-Bayesian non-asymptotic bounds for two types of prior for the score parameters: a Gaussian prior, and a spike-and-slab prior; the latter makes it possible to perform feature selection. One important advantage of our approach is that it is amenable to powerful Bayesian computational tools. We derive in particular a Sequential Monte Carlo algorithm, as an efficient method which may be used as a gold standard, and an Expectation-Propagation algorithm, as a much faster but approximate method. We also extend our method to a class of non-linear score functions, essentially leading to a nonparametric procedure, by considering a Gaussian process prior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge