Logarithmic Smoothing for Pessimistic Off-Policy Evaluation, Selection and Learning

This work investigates the offline formulation of the contextual bandit problem, where the goal is to leverage past interactions collected under a behavior policy to evaluate, select, and learn new, potentially better-performing, policies. Motivated by critical applications, we move beyond point estimators. Instead, we adopt the principle of pessimism where we construct upper bounds that assess a policy's worst-case performance, enabling us to confidently select and learn improved policies. Precisely, we introduce novel, fully empirical concentration bounds for a broad class of importance weighting risk estimators. These bounds are general enough to cover most existing estimators and pave the way for the development of new ones. In particular, our pursuit of the tightest bound within this class motivates a novel estimator (LS), that logarithmically smooths large importance weights. The bound for LS is provably tighter than all its competitors, and naturally results in improved policy selection and learning strategies. Extensive policy evaluation, selection, and learning experiments highlight the versatility and favorable performance of LS.

A connection between Tempering and Entropic Mirror Descent

This paper explores the connections between tempering (for Sequential Monte Carlo; SMC) and entropic mirror descent to sample from a target probability distribution whose unnormalized density is known. We establish that tempering SMC is a numerical approximation of entropic mirror descent applied to the Kullback-Leibler (KL) divergence and obtain convergence rates for the tempering iterates. Our result motivates the tempering iterates from an optimization point of view, showing that tempering can be used as an alternative to Langevin-based algorithms to minimize the KL divergence. We exploit the connection between tempering and mirror descent iterates to justify common practices in SMC and propose improvements to algorithms in literature.

Fast Slate Policy Optimization: Going Beyond Plackett-Luce

An increasingly important building block of large scale machine learning systems is based on returning slates; an ordered lists of items given a query. Applications of this technology include: search, information retrieval and recommender systems. When the action space is large, decision systems are restricted to a particular structure to complete online queries quickly. This paper addresses the optimization of these large scale decision systems given an arbitrary reward function. We cast this learning problem in a policy optimization framework and propose a new class of policies, born from a novel relaxation of decision functions. This results in a simple, yet efficient learning algorithm that scales to massive action spaces. We compare our method to the commonly adopted Plackett-Luce policy class and demonstrate the effectiveness of our approach on problems with action space sizes in the order of millions.

PAC-Bayesian Offline Contextual Bandits With Guarantees

This paper introduces a new principled approach for offline policy optimisation in contextual bandits. For two well-established risk estimators, we propose novel generalisation bounds able to confidently improve upon the logging policy offline. Unlike previous work, our approach does not require tuning hyperparameters on held-out sets, and enables deployment with no prior A/B testing. This is achieved by analysing the problem through the PAC-Bayesian lens; mainly, we let go of traditional policy parametrisation (e.g. softmax) and instead interpret the policies as mixtures of deterministic strategies. We demonstrate through extensive experiments evidence of our bounds tightness and the effectiveness of our approach in practical scenarios.

Computational Doob's $h$-transforms for Online Filtering of Discretely Observed Diffusions

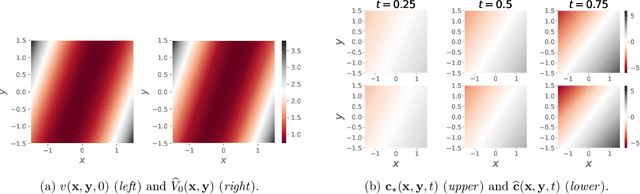
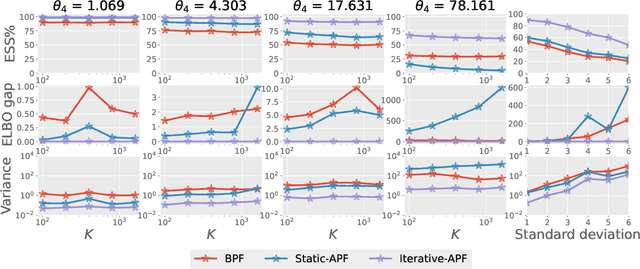
This paper is concerned with online filtering of discretely observed nonlinear diffusion processes. Our approach is based on the fully adapted auxiliary particle filter, which involves Doob's $h$-transforms that are typically intractable. We propose a computational framework to approximate these $h$-transforms by solving the underlying backward Kolmogorov equations using nonlinear Feynman-Kac formulas and neural networks. The methodology allows one to train a locally optimal particle filter prior to the data-assimilation procedure. Numerical experiments illustrate that the proposed approach can be orders of magnitude more efficient than the bootstrap particle filter in the regime of highly informative observations, when the observations are extreme under the model, and if the state dimension is large.

De-Sequentialized Monte Carlo: a parallel-in-time particle smoother

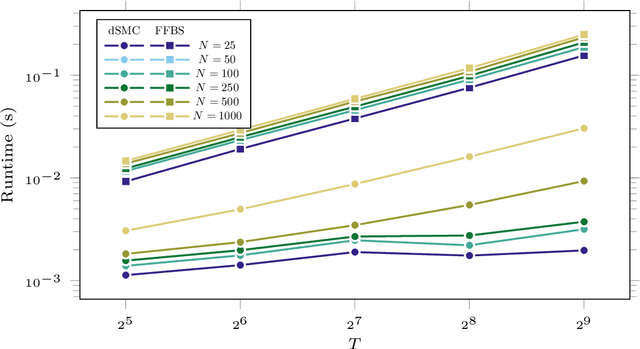
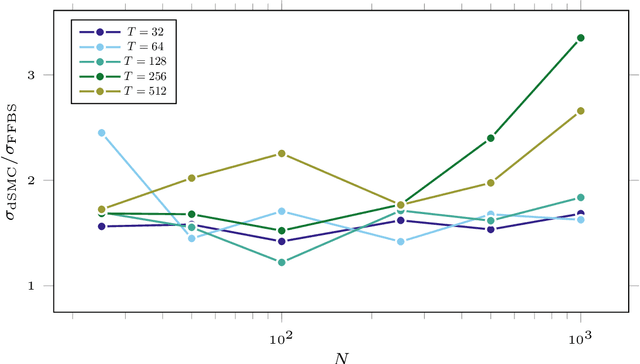
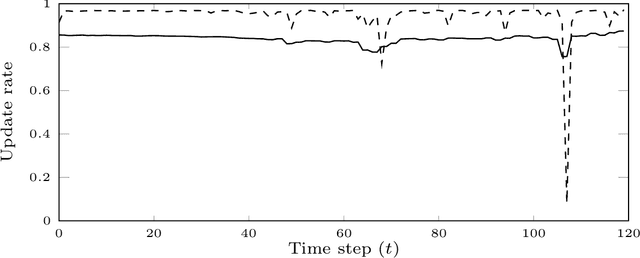
Particle smoothers are SMC (Sequential Monte Carlo) algorithms designed to approximate the joint distribution of the states given observations from a state-space model. We propose dSMC (de-Sequentialized Monte Carlo), a new particle smoother that is able to process $T$ observations in $\mathcal{O}(\log T)$ time on parallel architecture. This compares favourably with standard particle smoothers, the complexity of which is linear in $T$. We derive $\mathcal{L}_p$ convergence results for dSMC, with an explicit upper bound, polynomial in $T$. We then discuss how to reduce the variance of the smoothing estimates computed by dSMC by (i) designing good proposal distributions for sampling the particles at the initialization of the algorithm, as well as by (ii) using lazy resampling to increase the number of particles used in dSMC. Finally, we design a particle Gibbs sampler based on dSMC, which is able to perform parameter inference in a state-space model at a $\mathcal{O}(\log(T))$ cost on parallel hardware.

Modelling dependency completion in sentence comprehension as a Bayesian hierarchical mixture process: A case study involving Chinese relative clauses

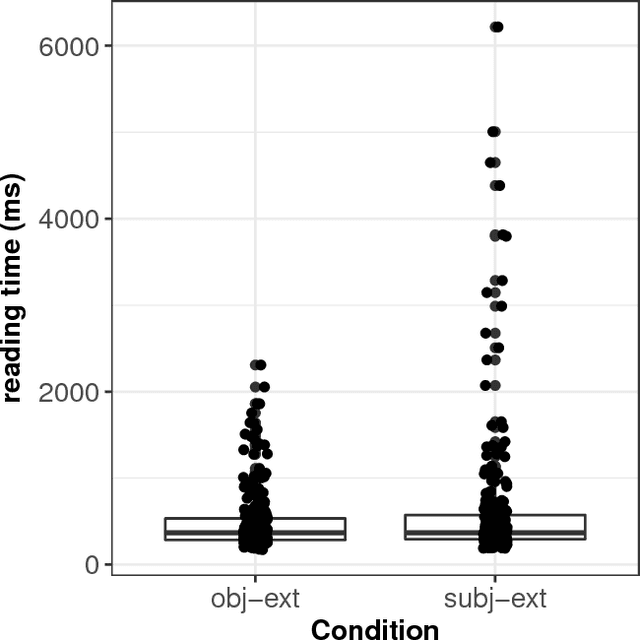
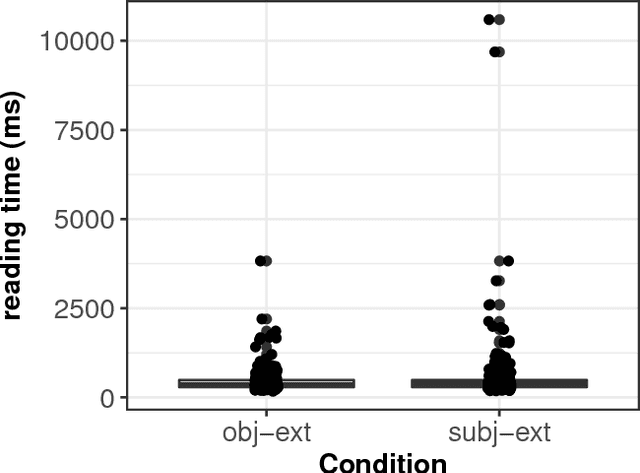
We present a case-study demonstrating the usefulness of Bayesian hierarchical mixture modelling for investigating cognitive processes. In sentence comprehension, it is widely assumed that the distance between linguistic co-dependents affects the latency of dependency resolution: the longer the distance, the longer the retrieval time (the distance-based account). An alternative theory, direct-access, assumes that retrieval times are a mixture of two distributions: one distribution represents successful retrievals (these are independent of dependency distance) and the other represents an initial failure to retrieve the correct dependent, followed by a reanalysis that leads to successful retrieval. We implement both models as Bayesian hierarchical models and show that the direct-access model explains Chinese relative clause reading time data better than the distance account.

On the properties of variational approximations of Gibbs posteriors

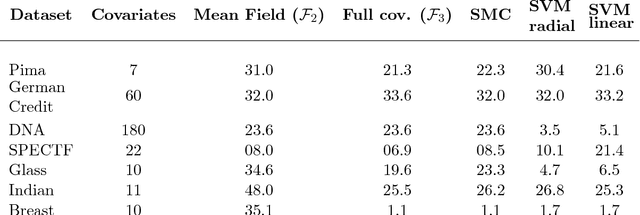
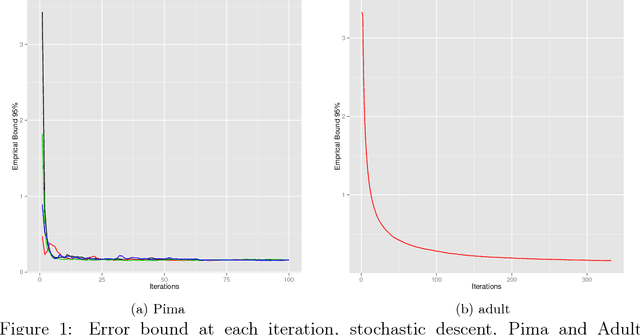
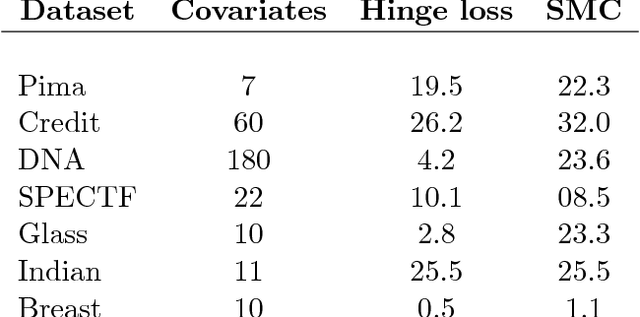
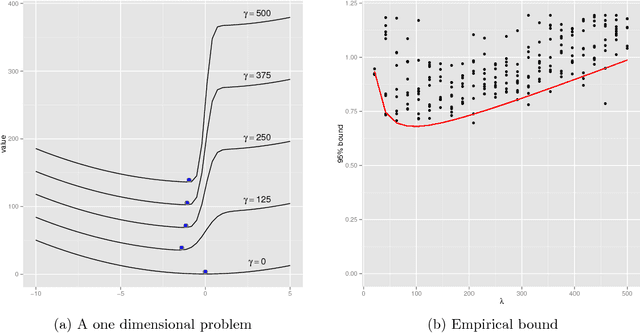
The PAC-Bayesian approach is a powerful set of techniques to derive non- asymptotic risk bounds for random estimators. The corresponding optimal distribution of estimators, usually called the Gibbs posterior, is unfortunately intractable. One may sample from it using Markov chain Monte Carlo, but this is often too slow for big datasets. We consider instead variational approximations of the Gibbs posterior, which are fast to compute. We undertake a general study of the properties of such approximations. Our main finding is that such a variational approximation has often the same rate of convergence as the original PAC-Bayesian procedure it approximates. We specialise our results to several learning tasks (classification, ranking, matrix completion),discuss how to implement a variational approximation in each case, and illustrate the good properties of said approximation on real datasets.

The Poisson transform for unnormalised statistical models

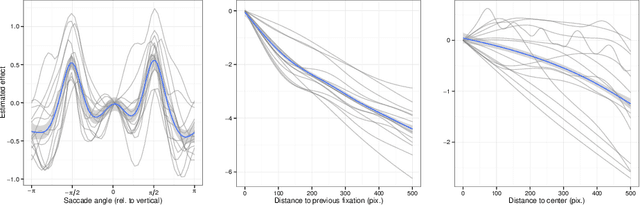
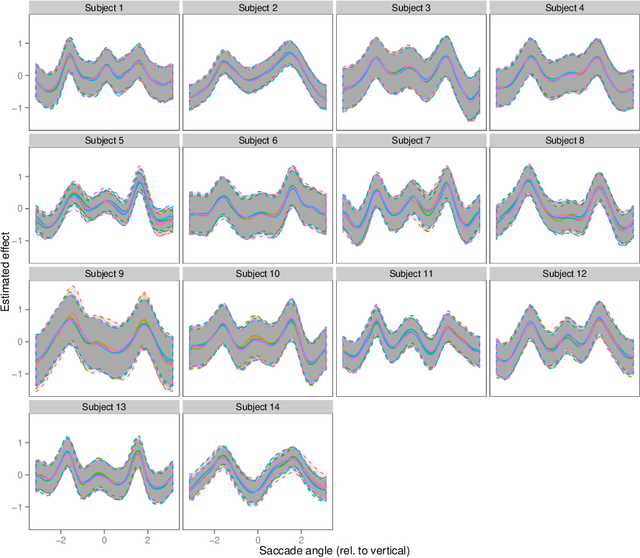
Contrary to standard statistical models, unnormalised statistical models only specify the likelihood function up to a constant. While such models are natural and popular, the lack of normalisation makes inference much more difficult. Here we show that inferring the parameters of a unnormalised model on a space $\Omega$ can be mapped onto an equivalent problem of estimating the intensity of a Poisson point process on $\Omega$. The unnormalised statistical model now specifies an intensity function that does not need to be normalised. Effectively, the normalisation constant may now be inferred as just another parameter, at no loss of information. The result can be extended to cover non-IID models, which includes for example unnormalised models for sequences of graphs (dynamical graphs), or for sequences of binary vectors. As a consequence, we prove that unnormalised parameteric inference in non-IID models can be turned into a semi-parametric estimation problem. Moreover, we show that the noise-contrastive divergence of Gutmann & Hyv\"arinen (2012) can be understood as an approximation of the Poisson transform, and extended to non-IID settings. We use our results to fit spatial Markov chain models of eye movements, where the Poisson transform allows us to turn a highly non-standard model into vanilla semi-parametric logistic regression.

Bayesian matrix completion: prior specification

Low-rank matrix estimation from incomplete measurements recently received increased attention due to the emergence of several challenging applications, such as recommender systems; see in particular the famous Netflix challenge. While the behaviour of algorithms based on nuclear norm minimization is now well understood, an as yet unexplored avenue of research is the behaviour of Bayesian algorithms in this context. In this paper, we briefly review the priors used in the Bayesian literature for matrix completion. A standard approach is to assign an inverse gamma prior to the singular values of a certain singular value decomposition of the matrix of interest; this prior is conjugate. However, we show that two other types of priors (again for the singular values) may be conjugate for this model: a gamma prior, and a discrete prior. Conjugacy is very convenient, as it makes it possible to implement either Gibbs sampling or Variational Bayes. Interestingly enough, the maximum a posteriori for these different priors is related to the nuclear norm minimization problems. We also compare all these priors on simulated datasets, and on the classical MovieLens and Netflix datasets.