Uniform-in-time Propagation-of-Chaos for Stein Variational Gradient Descent

We study uniform-in-time propagation-of-chaos for continuous-time Stein Variational Gradient Descent (SVGD). Classical finite-time propagation-of-chaos estimates for mean-field systems typically deteriorate rapidly with time and therefore do not directly explain the long-time relation between the finite-particle system and its mean-field limit. We obtain two complementary classes of uniform-in-time propagation-of-chaos results. For broad distributional metrics, we introduce a cutoff strategy which combines finite-time propagation-of-chaos estimates up to an $N$-dependent horizon with independent quantitative long-time convergence estimates for the finite-particle and mean-field SVGD flows. This yields uniform-in-averaging-time propagation-of-chaos bounds in Langevin kernel Stein discrepancy, Wasserstein-1 distance, and Wasserstein-2 distance, with logarithmic or iterated-logarithmic rates depending on the metric, target and kernel class. We also develop a finite-dimensional theory for matrix-valued finite-rank kernels. For Gaussian targets with bilinear kernels, the SVGD dynamics close exactly on first and second moments, yielding genuine uniform-in-physical-time parametric propagation-of-chaos rates in finite-dimensional Stein-feature metrics. We then prove a conjugacy principle showing that these feature-level estimates transfer to conjugate target-kernel pairs under orientation-preserving diffeomorphisms, thereby extending the theory to broad classes of nonlinear, including multimodal, targets. Together, these results highlight the contrast between generic distributional metrics, for which our general approach yields logarithmic rates, and closed finite-dimensional Stein observables, for which parametric $N^{-1/2}$ propagation-of-chaos rates persist uniformly in time.

Highly Data Parallelizable Estimation of the Sliced-Wasserstein Distance Using Cumulative Distribution Functions

The Sliced Wasserstein (SW) distance has emerged as a computationally attractive alternative to the Wasserstein distance by leveraging one-dimensional optimal transport along random projections. Standard estimators of the SW distance rely on Monte Carlo averages of one-dimensional Wasserstein distances computed via quantile functions, which require sorting projected samples and access to full datasets. In this work, we introduce a new class of estimators for the Sliced Wasserstein distance based on cumulative distribution functions (CDFs) of projected measures, that avoid sorting and scale via massive dataset parallelism. This class includes several estimators, some of them being indexed by hyperparameters controlling their variance or smoothness. We show that they are especially well suited to scenarios in which CDFs are more tractable than quantile functions, such as mixtures of Gaussians, and moreover that they are also naturally compatible with federated learning, since CDFs of projected data can be computed and aggregated locally without requiring the exchange of raw samples.

A Unifying View of Variational Generative Wasserstein Flows

Many modern generative models can be viewed as minimizing divergences between probability distributions, yet they rely on different algorithmic and geometric principles. Wasserstein gradient flows provide a continuous-time formulation for optimizing over distributions, and can be approximated through their implicit discretization via the Jordan-Kinderlehrer-Otto (JKO) scheme. In this work, we present a unified theoretical framework for generative modeling based on Wasserstein gradient flows, which we refer to as Generative Wasserstein Flows (GWF). We show that a broad class of existing methods can be derived as instances of parametric JKO schemes for $f$-divergence objectives, and we establish equivalences between several recently proposed algorithms. We extend this framework beyond f-divergence to Integral Probability Metrics and squared Maximum Mean Discrepancy, deriving new JKO-based generative algorithms, and clarifying their connections with GANs. We study empirically the impact of the JKO regularization for a wide set of objectives. Finally, we analyze parametric Wasserstein flows, where the dynamics are restricted to distributions induced by parametrized maps.

Evaluating the Relevance of Uncertainty Estimators for LLM Hallucination

Large language models (LLMs) are prone to hallucinations, i.e., statements unsupported by the input or training data, hindering reliable deployment. In parallel, numerous uncertainty estimation (UE) methods have been proposed to quantify model confidence and are often implicitly treated as proxies for model failure. However, the relationship between uncertainty and hallucinations remains insufficiently characterized. We present a systematic empirical study of the association between uncertainty estimators and hallucinations in LLMs. Rather than assuming this association, we evaluate directly when and to what extent it holds. We consider a diverse set of uncertainty estimators, including information-theoretic, sampling-based, and reflexive estimators, and examine their behavior across hallucination settings. Our experiments cover both intrinsic hallucinations (violations of input faithfulness) and extrinsic hallucinations (unsupported claims relative to training data), using four complementary benchmarks, including RAGTruth and HalluLens. We find that the association is highly variable and often weak, depending on the hallucination type and the LLM under evaluation. These results challenge the use of uncertainty as a direct signal of hallucination and clarify when it provides actionable information.

Generalized Discrete Diffusion from Snapshots

We introduce Generalized Discrete Diffusion from Snapshots (GDDS), a unified framework for discrete diffusion modeling that supports arbitrary noising processes over large discrete state spaces. Our formulation encompasses all existing discrete diffusion approaches, while allowing significantly greater flexibility in the choice of corruption dynamics. The forward noising process relies on uniformization and enables fast arbitrary corruption. For the reverse process, we derive a simple evidence lower bound (ELBO) based on snapshot latents, instead of the entire noising path, that allows efficient training of standard generative modeling architectures with clear probabilistic interpretation. Our experiments on large-vocabulary discrete generation tasks suggest that the proposed framework outperforms existing discrete diffusion methods in terms of training efficiency and generation quality, and beats autoregressive models for the first time at this scale. We provide the code along with a blog post on the project page : \href{https://oussamazekri.fr/gdds}{https://oussamazekri.fr/gdds}.

Kernel Trace Distance: Quantum Statistical Metric between Measures through RKHS Density Operators

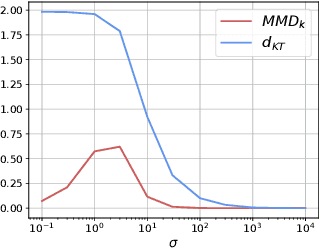
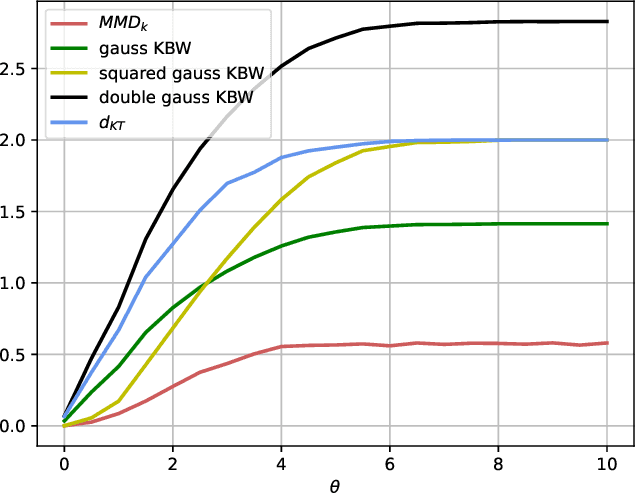
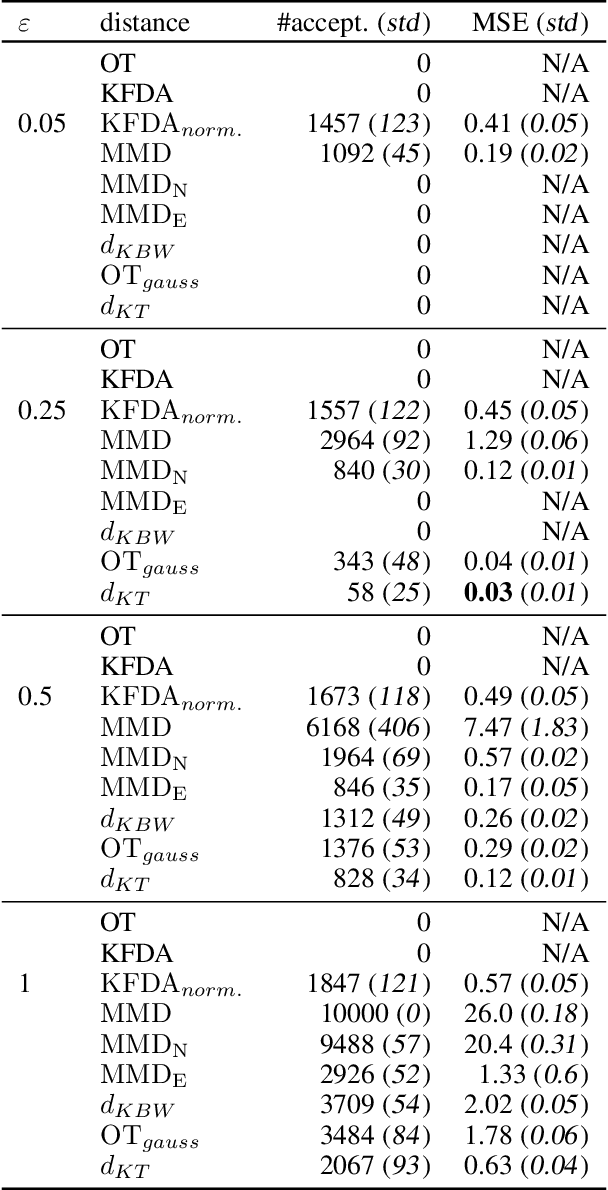
Distances between probability distributions are a key component of many statistical machine learning tasks, from two-sample testing to generative modeling, among others. We introduce a novel distance between measures that compares them through a Schatten norm of their kernel covariance operators. We show that this new distance is an integral probability metric that can be framed between a Maximum Mean Discrepancy (MMD) and a Wasserstein distance. In particular, we show that it avoids some pitfalls of MMD, by being more discriminative and robust to the choice of hyperparameters. Moreover, it benefits from some compelling properties of kernel methods, that can avoid the curse of dimensionality for their sample complexity. We provide an algorithm to compute the distance in practice by introducing an extension of kernel matrix for difference of distributions that could be of independent interest. Those advantages are illustrated by robust approximate Bayesian computation under contamination as well as particle flow simulations.

Variational Inference with Mixtures of Isotropic Gaussians

Variational inference (VI) is a popular approach in Bayesian inference, that looks for the best approximation of the posterior distribution within a parametric family, minimizing a loss that is typically the (reverse) Kullback-Leibler (KL) divergence. In this paper, we focus on the following parametric family: mixtures of isotropic Gaussians (i.e., with diagonal covariance matrices proportional to the identity) and uniform weights. We develop a variational framework and provide efficient algorithms suited for this family. In contrast with mixtures of Gaussian with generic covariance matrices, this choice presents a balance between accurate approximations of multimodal Bayesian posteriors, while being memory and computationally efficient. Our algorithms implement gradient descent on the location of the mixture components (the modes of the Gaussians), and either (an entropic) Mirror or Bures descent on their variance parameters. We illustrate the performance of our algorithms on numerical experiments.

Flowing Datasets with Wasserstein over Wasserstein Gradient Flows

Many applications in machine learning involve data represented as probability distributions. The emergence of such data requires radically novel techniques to design tractable gradient flows on probability distributions over this type of (infinite-dimensional) objects. For instance, being able to flow labeled datasets is a core task for applications ranging from domain adaptation to transfer learning or dataset distillation. In this setting, we propose to represent each class by the associated conditional distribution of features, and to model the dataset as a mixture distribution supported on these classes (which are themselves probability distributions), meaning that labeled datasets can be seen as probability distributions over probability distributions. We endow this space with a metric structure from optimal transport, namely the Wasserstein over Wasserstein (WoW) distance, derive a differential structure on this space, and define WoW gradient flows. The latter enables to design dynamics over this space that decrease a given objective functional. We apply our framework to transfer learning and dataset distillation tasks, leveraging our gradient flow construction as well as novel tractable functionals that take the form of Maximum Mean Discrepancies with Sliced-Wasserstein based kernels between probability distributions.

DDEQs: Distributional Deep Equilibrium Models through Wasserstein Gradient Flows

Deep Equilibrium Models (DEQs) are a class of implicit neural networks that solve for a fixed point of a neural network in their forward pass. Traditionally, DEQs take sequences as inputs, but have since been applied to a variety of data. In this work, we present Distributional Deep Equilibrium Models (DDEQs), extending DEQs to discrete measure inputs, such as sets or point clouds. We provide a theoretically grounded framework for DDEQs. Leveraging Wasserstein gradient flows, we show how the forward pass of the DEQ can be adapted to find fixed points of discrete measures under permutation-invariance, and derive adequate network architectures for DDEQs. In experiments, we show that they can compete with state-of-the-art models in tasks such as point cloud classification and point cloud completion, while being significantly more parameter-efficient.

Properties of Wasserstein Gradient Flows for the Sliced-Wasserstein Distance

In this paper, we investigate the properties of the Sliced Wasserstein Distance (SW) when employed as an objective functional. The SW metric has gained significant interest in the optimal transport and machine learning literature, due to its ability to capture intricate geometric properties of probability distributions while remaining computationally tractable, making it a valuable tool for various applications, including generative modeling and domain adaptation. Our study aims to provide a rigorous analysis of the critical points arising from the optimization of the SW objective. By computing explicit perturbations, we establish that stable critical points of SW cannot concentrate on segments. This stability analysis is crucial for understanding the behaviour of optimization algorithms for models trained using the SW objective. Furthermore, we investigate the properties of the SW objective, shedding light on the existence and convergence behavior of critical points. We illustrate our theoretical results through numerical experiments.