Guided Speculative Inference for Efficient Test-Time Alignment of LLMs

We propose Guided Speculative Inference (GSI), a novel algorithm for efficient reward-guided decoding in large language models. GSI combines soft best-of-$n$ test-time scaling with a reward model $r(x,y)$ and speculative samples from a small auxiliary model $\pi_S(y\mid x)$. We provably approximate the optimal tilted policy $\pi_{\beta,B}(y\mid x) \propto \pi_B(y\mid x)\exp(\beta\,r(x,y))$ of soft best-of-$n$ under the primary model $\pi_B$. We derive a theoretical bound on the KL divergence between our induced distribution and the optimal policy. In experiments on reasoning benchmarks (MATH500, OlympiadBench, Minerva Math), our method achieves higher accuracy than standard soft best-of-$n$ with $\pi_S$ and reward-guided speculative decoding (Liao et al., 2025), and in certain settings even outperforms soft best-of-$n$ with $\pi_B$. The code is available at https://github.com/j-geuter/GSI .

Decomposing Elements of Problem Solving: What "Math" Does RL Teach?

Mathematical reasoning tasks have become prominent benchmarks for assessing the reasoning capabilities of LLMs, especially with reinforcement learning (RL) methods such as GRPO showing significant performance gains. However, accuracy metrics alone do not support fine-grained assessment of capabilities and fail to reveal which problem-solving skills have been internalized. To better understand these capabilities, we propose to decompose problem solving into fundamental capabilities: Plan (mapping questions to sequences of steps), Execute (correctly performing solution steps), and Verify (identifying the correctness of a solution). Empirically, we find that GRPO mainly enhances the execution skill-improving execution robustness on problems the model already knows how to solve-a phenomenon we call temperature distillation. More importantly, we show that RL-trained models struggle with fundamentally new problems, hitting a 'coverage wall' due to insufficient planning skills. To explore RL's impact more deeply, we construct a minimal, synthetic solution-tree navigation task as an analogy for mathematical problem-solving. This controlled setup replicates our empirical findings, confirming RL primarily boosts execution robustness. Importantly, in this setting, we identify conditions under which RL can potentially overcome the coverage wall through improved exploration and generalization to new solution paths. Our findings provide insights into the role of RL in enhancing LLM reasoning, expose key limitations, and suggest a path toward overcoming these barriers. Code is available at https://github.com/cfpark00/RL-Wall.

Causal integration of chemical structures improves representations of microscopy images for morphological profiling

Recent advances in self-supervised deep learning have improved our ability to quantify cellular morphological changes in high-throughput microscopy screens, a process known as morphological profiling. However, most current methods only learn from images, despite many screens being inherently multimodal, as they involve both a chemical or genetic perturbation as well as an image-based readout. We hypothesized that incorporating chemical compound structure during self-supervised pre-training could improve learned representations of images in high-throughput microscopy screens. We introduce a representation learning framework, MICON (Molecular-Image Contrastive Learning), that models chemical compounds as treatments that induce counterfactual transformations of cell phenotypes. MICON significantly outperforms classical hand-crafted features such as CellProfiler and existing deep-learning-based representation learning methods in challenging evaluation settings where models must identify reproducible effects of drugs across independent replicates and data-generating centers. We demonstrate that incorporating chemical compound information into the learning process provides consistent improvements in our evaluation setting and that modeling compounds specifically as treatments in a causal framework outperforms approaches that directly align images and compounds in a single representation space. Our findings point to a new direction for representation learning in morphological profiling, suggesting that methods should explicitly account for the multimodal nature of microscopy screening data.

To Backtrack or Not to Backtrack: When Sequential Search Limits Model Reasoning

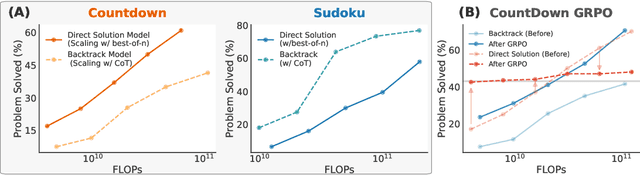
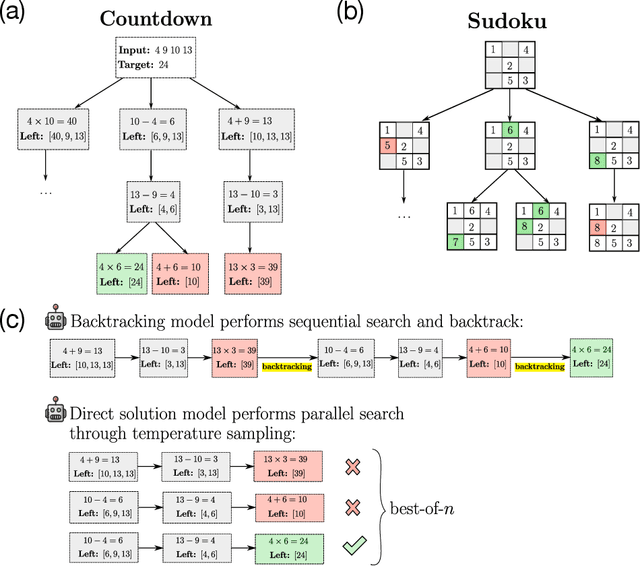
Recent advancements in large language models have significantly improved their reasoning abilities, particularly through techniques involving search and backtracking. Backtracking naturally scales test-time compute by enabling sequential, linearized exploration via long chain-of-thought (CoT) generation. However, this is not the only strategy for scaling test-time compute: parallel sampling with best-of-n selection provides an alternative that generates diverse solutions simultaneously. Despite the growing adoption of sequential search, its advantages over parallel sampling--especially under a fixed compute budget remain poorly understood. In this paper, we systematically compare these two approaches on two challenging reasoning tasks: CountDown and Sudoku. Surprisingly, we find that sequential search underperforms parallel sampling on CountDown but outperforms it on Sudoku, suggesting that backtracking is not universally beneficial. We identify two factors that can cause backtracking to degrade performance: (1) training on fixed search traces can lock models into suboptimal strategies, and (2) explicit CoT supervision can discourage "implicit" (non-verbalized) reasoning. Extending our analysis to reinforcement learning (RL), we show that models with backtracking capabilities benefit significantly from RL fine-tuning, while models without backtracking see limited, mixed gains. Together, these findings challenge the assumption that backtracking universally enhances LLM reasoning, instead revealing a complex interaction between task structure, training data, model scale, and learning paradigm.

DDEQs: Distributional Deep Equilibrium Models through Wasserstein Gradient Flows

Deep Equilibrium Models (DEQs) are a class of implicit neural networks that solve for a fixed point of a neural network in their forward pass. Traditionally, DEQs take sequences as inputs, but have since been applied to a variety of data. In this work, we present Distributional Deep Equilibrium Models (DDEQs), extending DEQs to discrete measure inputs, such as sets or point clouds. We provide a theoretically grounded framework for DDEQs. Leveraging Wasserstein gradient flows, we show how the forward pass of the DEQ can be adapted to find fixed points of discrete measures under permutation-invariance, and derive adequate network architectures for DDEQs. In experiments, we show that they can compete with state-of-the-art models in tasks such as point cloud classification and point cloud completion, while being significantly more parameter-efficient.

IGDA: Interactive Graph Discovery through Large Language Model Agents

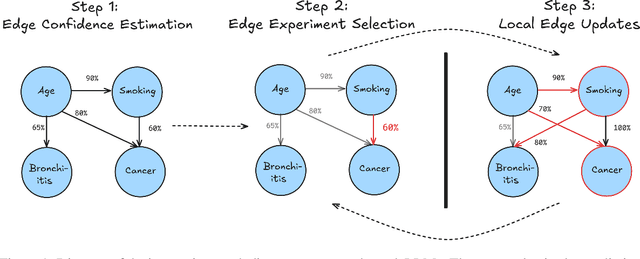
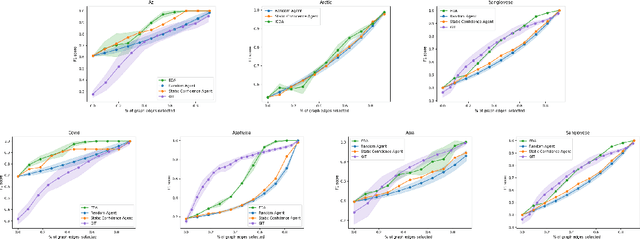
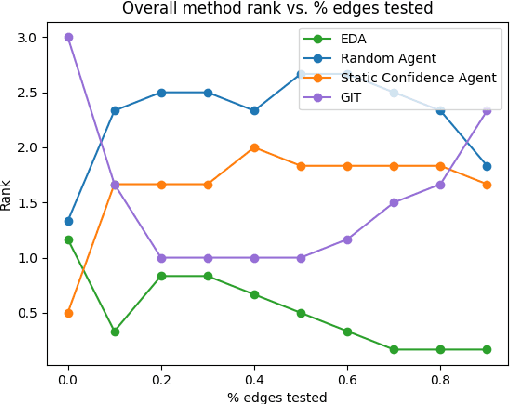
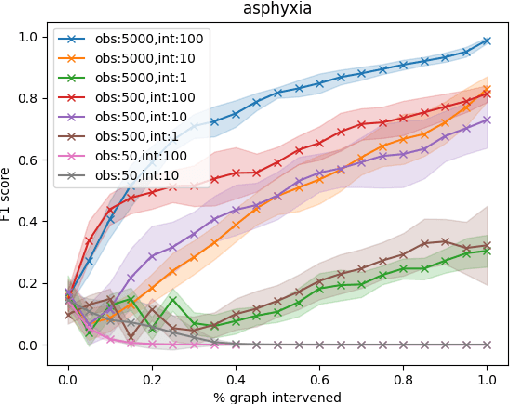
Large language models ($\textbf{LLMs}$) have emerged as a powerful method for discovery. Instead of utilizing numerical data, LLMs utilize associated variable $\textit{semantic metadata}$ to predict variable relationships. Simultaneously, LLMs demonstrate impressive abilities to act as black-box optimizers when given an objective $f$ and sequence of trials. We study LLMs at the intersection of these two capabilities by applying LLMs to the task of $\textit{interactive graph discovery}$: given a ground truth graph $G^*$ capturing variable relationships and a budget of $I$ edge experiments over $R$ rounds, minimize the distance between the predicted graph $\hat{G}_R$ and $G^*$ at the end of the $R$-th round. To solve this task we propose $\textbf{IGDA}$, a LLM-based pipeline incorporating two key components: 1) an LLM uncertainty-driven method for edge experiment selection 2) a local graph update strategy utilizing binary feedback from experiments to improve predictions for unselected neighboring edges. Experiments on eight different real-world graphs show our approach often outperforms all baselines including a state-of-the-art numerical method for interactive graph discovery. Further, we conduct a rigorous series of ablations dissecting the impact of each pipeline component. Finally, to assess the impact of memorization, we apply our interactive graph discovery strategy to a complex, new (as of July 2024) causal graph on protein transcription factors, finding strong performance in a setting where memorization is impossible. Overall, our results show IGDA to be a powerful method for graph discovery complementary to existing numerically driven approaches.

Distributional Scaling Laws for Emergent Capabilities

In this paper, we explore the nature of sudden breakthroughs in language model performance at scale, which stands in contrast to smooth improvements governed by scaling laws. While advocates of "emergence" view abrupt performance gains as capabilities unlocking at specific scales, others have suggested that they are produced by thresholding effects and alleviated by continuous metrics. We propose that breakthroughs are instead driven by continuous changes in the probability distribution of training outcomes, particularly when performance is bimodally distributed across random seeds. In synthetic length generalization tasks, we show that different random seeds can produce either highly linear or emergent scaling trends. We reveal that sharp breakthroughs in metrics are produced by underlying continuous changes in their distribution across seeds. Furthermore, we provide a case study of inverse scaling and show that even as the probability of a successful run declines, the average performance of a successful run continues to increase monotonically. We validate our distributional scaling framework on realistic settings by measuring MMLU performance in LLM populations. These insights emphasize the role of random variation in the effect of scale on LLM capabilities.

Sometimes I am a Tree: Data Drives Unstable Hierarchical Generalization

Neural networks often favor shortcut heuristics based on surface-level patterns. As one example, language models (LMs) behave like n-gram models early in training. However, to correctly apply grammatical rules, LMs must rely on hierarchical syntactic representations instead of n-grams. In this work, we use cases studies of English grammar to explore how latent structure in training data drives models toward improved out-of-distribution (OOD) generalization.We then investigate how data composition can lead to inconsistent OOD behavior across random seeds and to unstable training dynamics. Our results show that models stabilize in their OOD behavior only when they fully commit to either a surface-level linear rule or a hierarchical rule. The hierarchical rule, furthermore, is induced by grammatically complex sequences with deep embedding structures, whereas the linear rule is induced by simpler sequences. When the data contains a mix of simple and complex examples, potential rules compete; each independent training run either stabilizes by committing to a single rule or remains unstable in its OOD behavior. These conditions lead `stable seeds' to cluster around simple rules, forming bimodal performance distributions across seeds. We also identify an exception to the relationship between stability and generalization: models which memorize patterns from low-diversity training data can overfit stably, with different rules for memorized and unmemorized patterns. Our findings emphasize the critical role of training data in shaping generalization patterns and how competition between data subsets contributes to inconsistent generalization outcomes across random seeds. Code is available at https://github.com/sunnytqin/concept_comp.git.

Adapting Language Models via Token Translation

Modern large language models use a fixed tokenizer to effectively compress text drawn from a source domain. However, applying the same tokenizer to a new target domain often leads to inferior compression, more costly inference, and reduced semantic alignment. To address this deficiency, we introduce Sparse Sinkhorn Token Translation (S2T2). S2T2 trains a tailored tokenizer for the target domain and learns to translate between target and source tokens, enabling more effective reuse of the pre-trained next-source-token predictor. In our experiments with finetuned English language models, S2T2 improves both the perplexity and the compression of out-of-domain protein sequences, outperforming direct finetuning with either the source or target tokenizer. In addition, we find that token translations learned for smaller, less expensive models can be directly transferred to larger, more powerful models to reap the benefits of S2T2 at lower cost.

Mixture of Parrots: Experts improve memorization more than reasoning

The Mixture-of-Experts (MoE) architecture enables a significant increase in the total number of model parameters with minimal computational overhead. However, it is not clear what performance tradeoffs, if any, exist between MoEs and standard dense transformers. In this paper, we show that as we increase the number of experts (while fixing the number of active parameters), the memorization performance consistently increases while the reasoning capabilities saturate. We begin by analyzing the theoretical limitations of MoEs at reasoning. We prove that there exist graph problems that cannot be solved by any number of experts of a certain width; however, the same task can be easily solved by a dense model with a slightly larger width. On the other hand, we find that on memory-intensive tasks, MoEs can effectively leverage a small number of active parameters with a large number of experts to memorize the data. We empirically validate these findings on synthetic graph problems and memory-intensive closed book retrieval tasks. Lastly, we pre-train a series of MoEs and dense transformers and evaluate them on commonly used benchmarks in math and natural language. We find that increasing the number of experts helps solve knowledge-intensive tasks, but fails to yield the same benefits for reasoning tasks.