Decomposing Elements of Problem Solving: What "Math" Does RL Teach?

Mathematical reasoning tasks have become prominent benchmarks for assessing the reasoning capabilities of LLMs, especially with reinforcement learning (RL) methods such as GRPO showing significant performance gains. However, accuracy metrics alone do not support fine-grained assessment of capabilities and fail to reveal which problem-solving skills have been internalized. To better understand these capabilities, we propose to decompose problem solving into fundamental capabilities: Plan (mapping questions to sequences of steps), Execute (correctly performing solution steps), and Verify (identifying the correctness of a solution). Empirically, we find that GRPO mainly enhances the execution skill-improving execution robustness on problems the model already knows how to solve-a phenomenon we call temperature distillation. More importantly, we show that RL-trained models struggle with fundamentally new problems, hitting a 'coverage wall' due to insufficient planning skills. To explore RL's impact more deeply, we construct a minimal, synthetic solution-tree navigation task as an analogy for mathematical problem-solving. This controlled setup replicates our empirical findings, confirming RL primarily boosts execution robustness. Importantly, in this setting, we identify conditions under which RL can potentially overcome the coverage wall through improved exploration and generalization to new solution paths. Our findings provide insights into the role of RL in enhancing LLM reasoning, expose key limitations, and suggest a path toward overcoming these barriers. Code is available at https://github.com/cfpark00/RL-Wall.

CT-OT Flow: Estimating Continuous-Time Dynamics from Discrete Temporal Snapshots

In many real-world scenarios, such as single-cell RNA sequencing, data are observed only as discrete-time snapshots spanning finite time intervals and subject to noisy timestamps, with no continuous trajectories available. Recovering the underlying continuous-time dynamics from these snapshots with coarse and noisy observation times is a critical and challenging task. We propose Continuous-Time Optimal Transport Flow (CT-OT Flow), which first infers high-resolution time labels via partial optimal transport and then reconstructs a continuous-time data distribution through a temporal kernel smoothing. This reconstruction enables accurate training of dynamics models such as ODEs and SDEs. CT-OT Flow consistently outperforms state-of-the-art methods on synthetic benchmarks and achieves lower reconstruction errors on real scRNA-seq and typhoon-track datasets. Our results highlight the benefits of explicitly modeling temporal discretization and timestamp uncertainty, offering an accurate and general framework for bridging discrete snapshots and continuous-time processes.

$\textit{New News}$: System-2 Fine-tuning for Robust Integration of New Knowledge

Humans and intelligent animals can effortlessly internalize new information ("news") and accurately extract the implications for performing downstream tasks. While large language models (LLMs) can achieve this through in-context learning (ICL) when the news is explicitly given as context, fine-tuning remains challenging for the models to consolidate learning in weights. In this paper, we introduce $\textit{New News}$, a dataset composed of hypothetical yet plausible news spanning multiple domains (mathematics, coding, discoveries, leaderboards, events), accompanied by downstream evaluation questions whose correct answers critically depend on understanding and internalizing the news. We first demonstrate a substantial gap between naive fine-tuning and in-context learning (FT-ICL gap) on our news dataset. To address this gap, we explore a suite of self-play data generation protocols -- paraphrases, implications and Self-QAs -- designed to distill the knowledge from the model with context into the weights of the model without the context, which we term $\textit{System-2 Fine-tuning}$ (Sys2-FT). We systematically evaluate ICL and Sys2-FT performance across data domains and model scales with the Qwen 2.5 family of models. Our results demonstrate that the self-QA protocol of Sys2-FT significantly improves models' in-weight learning of the news. Furthermore, we discover the $\textit{contexual shadowing effect}$, where training with the news $\textit{in context}$ followed by its rephrases or QAs degrade learning of the news. Finally, we show preliminary evidence of an emerging scaling law of Sys2-FT.

A ghost mechanism: An analytical model of abrupt learning

\emph{Abrupt learning} is commonly observed in neural networks, where long plateaus in network performance are followed by rapid convergence to a desirable solution. Yet, despite its common occurrence, the complex interplay of task, network architecture, and learning rule has made it difficult to understand the underlying mechanisms. Here, we introduce a minimal dynamical system trained on a delayed-activation task and demonstrate analytically how even a one-dimensional system can exhibit abrupt learning through ghost points rather than bifurcations. Through our toy model, we show that the emergence of a ghost point destabilizes learning dynamics. We identify a critical learning rate that prevents learning through two distinct loss landscape features: a no-learning zone and an oscillatory minimum. Testing these predictions in recurrent neural networks (RNNs), we confirm that ghost points precede abrupt learning and accompany the destabilization of learning. We demonstrate two complementary remedies: lowering the model output confidence prevents the network from getting stuck in no-learning zones, while increasing trainable ranks beyond task requirements (\textit{i.e.}, adding sloppy parameters) provides more stable learning trajectories. Our model reveals a bifurcation-free mechanism for abrupt learning and illustrates the importance of both deliberate uncertainty and redundancy in stabilizing learning dynamics.

ICLR: In-Context Learning of Representations

Recent work has demonstrated that semantics specified by pretraining data influence how representations of different concepts are organized in a large language model (LLM). However, given the open-ended nature of LLMs, e.g., their ability to in-context learn, we can ask whether models alter these pretraining semantics to adopt alternative, context-specified ones. Specifically, if we provide in-context exemplars wherein a concept plays a different role than what the pretraining data suggests, do models reorganize their representations in accordance with these novel semantics? To answer this question, we take inspiration from the theory of conceptual role semantics and define a toy "graph tracing" task wherein the nodes of the graph are referenced via concepts seen during training (e.g., apple, bird, etc.) and the connectivity of the graph is defined via some predefined structure (e.g., a square grid). Given exemplars that indicate traces of random walks on the graph, we analyze intermediate representations of the model and find that as the amount of context is scaled, there is a sudden re-organization from pretrained semantic representations to in-context representations aligned with the graph structure. Further, we find that when reference concepts have correlations in their semantics (e.g., Monday, Tuesday, etc.), the context-specified graph structure is still present in the representations, but is unable to dominate the pretrained structure. To explain these results, we analogize our task to energy minimization for a predefined graph topology, providing evidence towards an implicit optimization process to infer context-specified semantics. Overall, our findings indicate scaling context-size can flexibly re-organize model representations, possibly unlocking novel capabilities.

Forking Paths in Neural Text Generation

Estimating uncertainty in Large Language Models (LLMs) is important for properly evaluating LLMs, and ensuring safety for users. However, prior approaches to uncertainty estimation focus on the final answer in generated text, ignoring intermediate steps that might dramatically impact the outcome. We hypothesize that there exist key forking tokens, such that re-sampling the system at those specific tokens, but not others, leads to very different outcomes. To test this empirically, we develop a novel approach to representing uncertainty dynamics across individual tokens of text generation, and applying statistical models to test our hypothesis. Our approach is highly flexible: it can be applied to any dataset and any LLM, without fine tuning or accessing model weights. We use our method to analyze LLM responses on 7 different tasks across 4 domains, spanning a wide range of typical use cases. We find many examples of forking tokens, including surprising ones such as punctuation marks, suggesting that LLMs are often just a single token away from saying something very different.

Competition Dynamics Shape Algorithmic Phases of In-Context Learning

In-Context Learning (ICL) has significantly expanded the general-purpose nature of large language models, allowing them to adapt to novel tasks using merely the inputted context. This has motivated a series of papers that analyze tractable synthetic domains and postulate precise mechanisms that may underlie ICL. However, the use of relatively distinct setups that often lack a sequence modeling nature to them makes it unclear how general the reported insights from such studies are. Motivated by this, we propose a synthetic sequence modeling task that involves learning to simulate a finite mixture of Markov chains. As we show, models trained on this task reproduce most well-known results on ICL, hence offering a unified setting for studying the concept. Building on this setup, we demonstrate we can explain a model's behavior by decomposing it into four broad algorithms that combine a fuzzy retrieval vs. inference approach with either unigram or bigram statistics of the context. These algorithms engage in a competition dynamics to dominate model behavior, with the precise experimental conditions dictating which algorithm ends up superseding others: e.g., we find merely varying context size or amount of training yields (at times sharp) transitions between which algorithm dictates the model behavior, revealing a mechanism that explains the transient nature of ICL. In this sense, we argue ICL is best thought of as a mixture of different algorithms, each with its own peculiarities, instead of a monolithic capability. This also implies that making general claims about ICL that hold universally across all settings may be infeasible.

Continuous-Time Analysis of Adaptive Optimization and Normalization

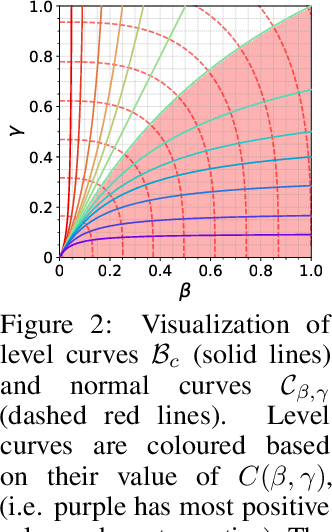
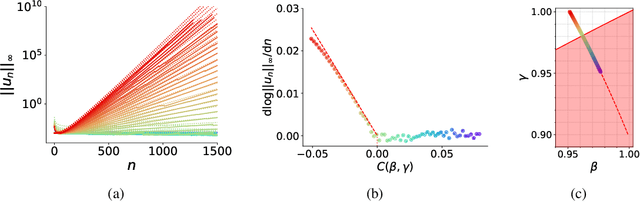
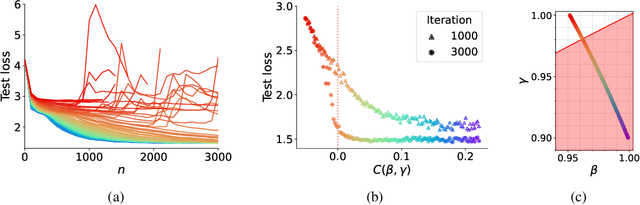
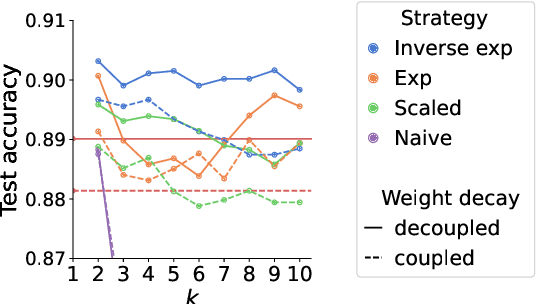
Adaptive optimization algorithms, particularly Adam and its variant AdamW, are fundamental components of modern deep learning. However, their training dynamics lack comprehensive theoretical understanding, with limited insight into why common practices - such as specific hyperparameter choices and normalization layers - contribute to successful generalization. This work presents a continuous-time formulation of Adam and AdamW, facilitating a tractable analysis of training dynamics that can shed light on such practical questions. We theoretically derive a stable region for Adam's hyperparameters $(\beta, \gamma)$ that ensures bounded updates, empirically verifying these predictions by observing unstable exponential growth of parameter updates outside this region. Furthermore, we theoretically justify the success of normalization layers by uncovering an implicit meta-adaptive effect of scale-invariant architectural components. This insight leads to an explicit optimizer, $2$-Adam, which we generalize to $k$-Adam - an optimizer that applies an adaptive normalization procedure $k$ times, encompassing Adam (corresponding to $k=1$) and Adam with a normalization layer (corresponding to $k=2$). Overall, our continuous-time formulation of Adam facilitates a principled analysis, offering deeper understanding of optimal hyperparameter choices and architectural decisions in modern deep learning.

Representation Shattering in Transformers: A Synthetic Study with Knowledge Editing

Knowledge Editing (KE) algorithms alter models' internal weights to perform targeted updates to incorrect, outdated, or otherwise unwanted factual associations. In order to better define the possibilities and limitations of these approaches, recent work has shown that applying KE can adversely affect models' factual recall accuracy and diminish their general reasoning abilities. While these studies give broad insights into the potential harms of KE algorithms, e.g., via performance evaluations on benchmarks, we argue little is understood as to why such destructive failures occur. Is it possible KE methods distort representations of concepts beyond the targeted fact, hence hampering abilities at broad? If so, what is the extent of this distortion? To take a step towards addressing such questions, we define a novel synthetic task wherein a Transformer is trained from scratch to internalize a ``structured'' knowledge graph. The structure enforces relationships between entities of the graph, such that editing a factual association has "trickling effects" on other entities in the graph (e.g., altering X's parent is Y to Z affects who X's siblings' parent is). Through evaluations of edited models and analysis of extracted representations, we show that KE inadvertently affects representations of entities beyond the targeted one, distorting relevant structures that allow a model to infer unseen knowledge about an entity. We call this phenomenon representation shattering and demonstrate that it results in degradation of factual recall and reasoning performance more broadly. To corroborate our findings in a more naturalistic setup, we perform preliminary experiments with a pretrained GPT-2-XL model and reproduce the representation shattering effect therein as well. Overall, our work yields a precise mechanistic hypothesis to explain why KE has adverse effects on model capabilities.

Dynamics of Concept Learning and Compositional Generalization

Prior work has shown that text-conditioned diffusion models can learn to identify and manipulate primitive concepts underlying a compositional data-generating process, enabling generalization to entirely novel, out-of-distribution compositions. Beyond performance evaluations, these studies develop a rich empirical phenomenology of learning dynamics, showing that models generalize sequentially, respecting the compositional hierarchy of the data-generating process. Moreover, concept-centric structures within the data significantly influence a model's speed of learning the ability to manipulate a concept. In this paper, we aim to better characterize these empirical results from a theoretical standpoint. Specifically, we propose an abstraction of prior work's compositional generalization problem by introducing a structured identity mapping (SIM) task, where a model is trained to learn the identity mapping on a Gaussian mixture with structurally organized centroids. We mathematically analyze the learning dynamics of neural networks trained on this SIM task and show that, despite its simplicity, SIM's learning dynamics capture and help explain key empirical observations on compositional generalization with diffusion models identified in prior work. Our theory also offers several new insights -- e.g., we find a novel mechanism for non-monotonic learning dynamics of test loss in early phases of training. We validate our new predictions by training a text-conditioned diffusion model, bridging our simplified framework and complex generative models. Overall, this work establishes the SIM task as a meaningful theoretical abstraction of concept learning dynamics in modern generative models.