Accuracy-Preserving Calibration via Statistical Modeling on Probability Simplex

Classification models based on deep neural networks (DNNs) must be calibrated to measure the reliability of predictions. Some recent calibration methods have employed a probabilistic model on the probability simplex. However, these calibration methods cannot preserve the accuracy of pre-trained models, even those with a high classification accuracy. We propose an accuracy-preserving calibration method using the Concrete distribution as the probabilistic model on the probability simplex. We theoretically prove that a DNN model trained on cross-entropy loss has optimality as the parameter of the Concrete distribution. We also propose an efficient method that synthetically generates samples for training probabilistic models on the probability simplex. We demonstrate that the proposed method can outperform previous methods in accuracy-preserving calibration tasks using benchmarks.

How many views does your deep neural network use for prediction?

The generalization ability of Deep Neural Networks (DNNs) is still not fully understood, despite numerous theoretical and empirical analyses. Recently, Allen-Zhu & Li (2023) introduced the concept of multi-views to explain the generalization ability of DNNs, but their main target is ensemble or distilled models, and no method for estimating multi-views used in a prediction of a specific input is discussed. In this paper, we propose Minimal Sufficient Views (MSVs), which is similar to multi-views but can be efficiently computed for real images. MSVs is a set of minimal and distinct features in an input, each of which preserves a model's prediction for the input. We empirically show that there is a clear relationship between the number of MSVs and prediction accuracy across models, including convolutional and transformer models, suggesting that a multi-view like perspective is also important for understanding the generalization ability of (non-ensemble or non-distilled) DNNs.

StyleDiff: Attribute Comparison Between Unlabeled Datasets in Latent Disentangled Space

One major challenge in machine learning applications is coping with mismatches between the datasets used in the development and those obtained in real-world applications. These mismatches may lead to inaccurate predictions and errors, resulting in poor product quality and unreliable systems. In this study, we propose StyleDiff to inform developers of the differences between the two datasets for the steady development of machine learning systems. Using disentangled image spaces obtained from recently proposed generative models, StyleDiff compares the two datasets by focusing on attributes in the images and provides an easy-to-understand analysis of the differences between the datasets. The proposed StyleDiff performs in $O (d N\log N)$, where $N$ is the size of the datasets and $d$ is the number of attributes, enabling the application to large datasets. We demonstrate that StyleDiff accurately detects differences between datasets and presents them in an understandable format using, for example, driving scenes datasets.

Partial Wasserstein Covering

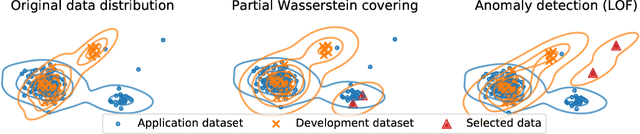
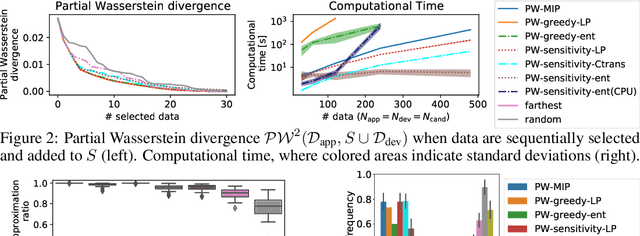
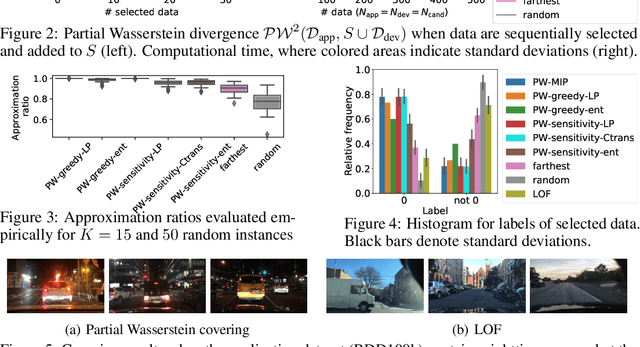
We consider a general task called partial Wasserstein covering with the goal of emulating a large dataset (e.g., application dataset) using a small dataset (e.g., development dataset) in terms of the empirical distribution by selecting a small subset from a candidate dataset and adding it to the small dataset. We model this task as a discrete optimization problem with partial Wasserstein divergence as an objective function. Although this problem is NP-hard, we prove that it has the submodular property, allowing us to use a greedy algorithm with a 0.63 approximation. However, the greedy algorithm is still inefficient because it requires linear programming for each objective function evaluation. To overcome this difficulty, we propose quasi-greedy algorithms for acceleration, which consist of a series of techniques such as sensitivity analysis based on strong duality and the so-called $C$-transform in the optimal transport field. Experimentally, we demonstrate that we can efficiently make two datasets similar in terms of partial Wasserstein divergence, including driving scene datasets.

Variational Monocular Depth Estimation for Reliability Prediction

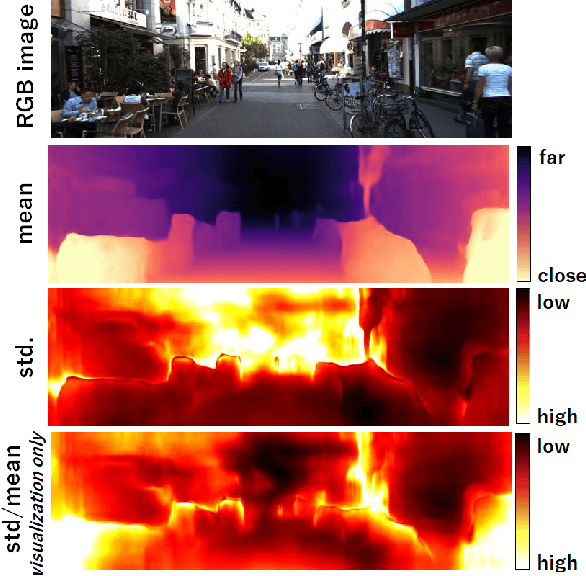
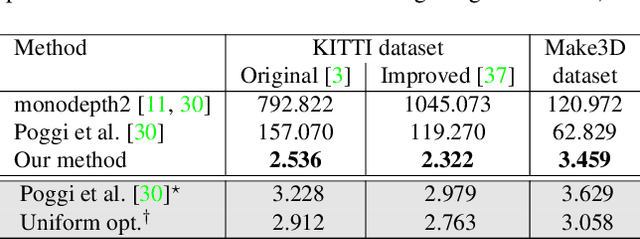
Self-supervised learning for monocular depth estimation is widely investigated as an alternative to supervised learning approach, that requires a lot of ground truths. Previous works have successfully improved the accuracy of depth estimation by modifying the model structure, adding objectives, and masking dynamic objects and occluded area. However, when using such estimated depth image in applications, such as autonomous vehicles, and robots, we have to uniformly believe the estimated depth at each pixel position. This could lead to fatal errors in performing the tasks, because estimated depth at some pixels may make a bigger mistake. In this paper, we theoretically formulate a variational model for the monocular depth estimation to predict the reliability of the estimated depth image. Based on the results, we can exclude the estimated depths with low reliability or refine them for actual use. The effectiveness of the proposed method is quantitatively and qualitatively demonstrated using the KITTI benchmark and Make3D dataset.

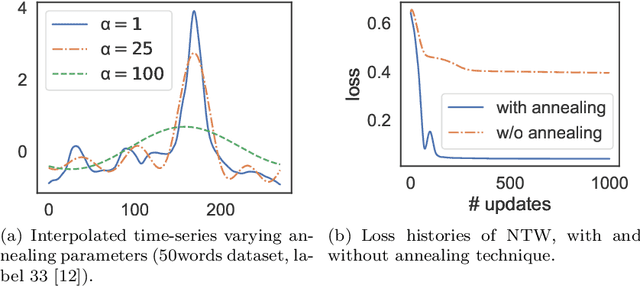
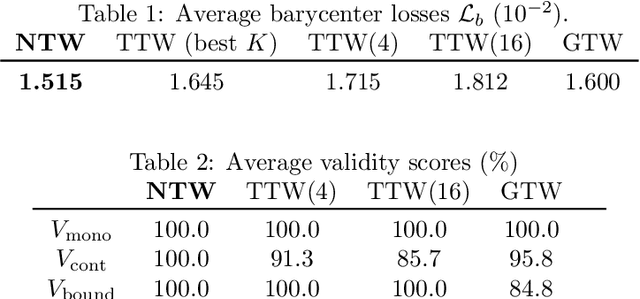
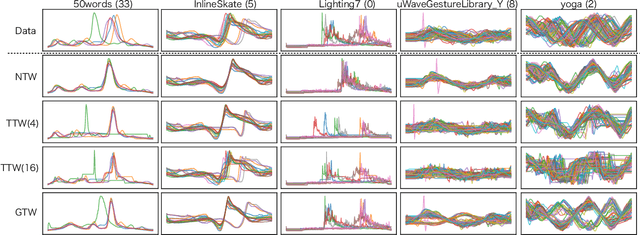
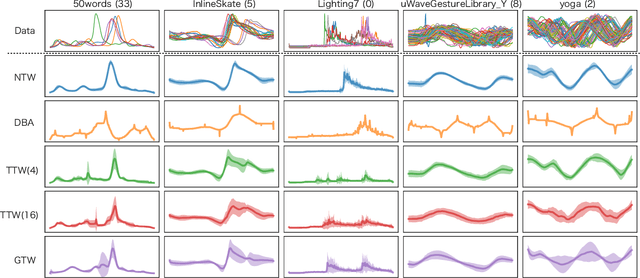
Neural Time Warping For Multiple Sequence Alignment

Multiple sequences alignment (MSA) is a traditional and challenging task for time-series analyses. The MSA problem is formulated as a discrete optimization problem and is typically solved by dynamic programming. However, the computational complexity increases exponentially with respect to the number of input sequences. In this paper, we propose neural time warping (NTW) that relaxes the original MSA to a continuous optimization and obtains the alignments using a neural network. The solution obtained by NTW is guaranteed to be a feasible solution for the original discrete optimization problem under mild conditions. Our experimental results show that NTW successfully aligns a hundred time-series and significantly outperforms existing methods for solving the MSA problem. In addition, we show a method for obtaining average time-series data as one of applications of NTW. Compared to the existing barycenters, the mean time series data retains the features of the input time-series data.

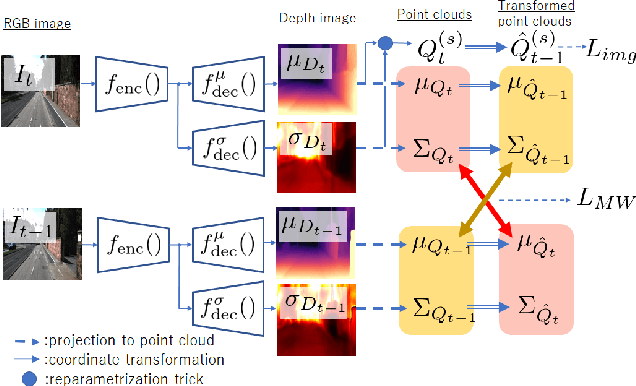
PLG-IN: Pluggable Geometric Consistency Loss with Wasserstein Distance in Monocular Depth Estimation

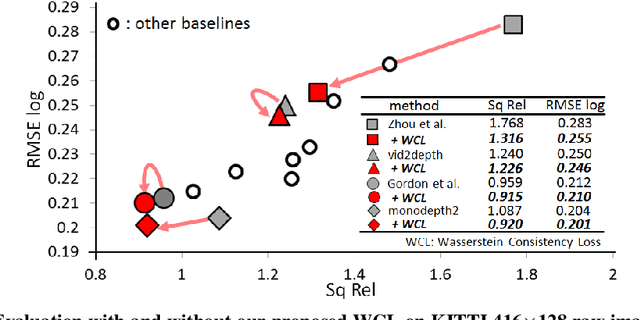
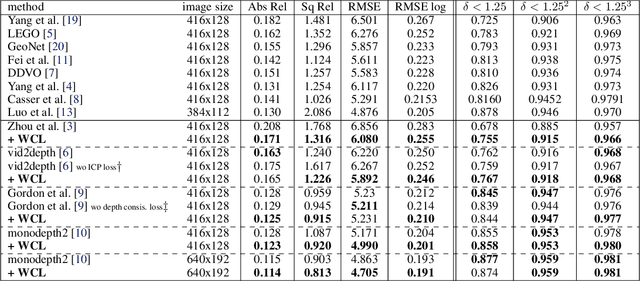
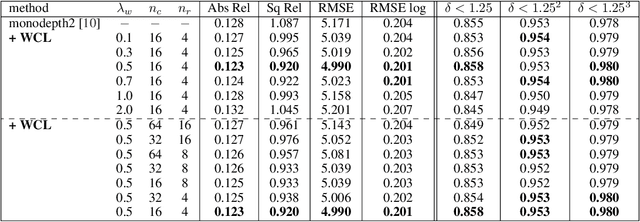
We propose a novel objective to penalize geometric inconsistencies, to improve the performance of depth estimation from monocular camera images. Our objective is designed with the Wasserstein distance between two point clouds estimated from images with different camera poses. The Wasserstein distance can impose a soft and symmetric coupling between two point clouds, which suitably keeps geometric constraints and leads differentiable objective. By adding our objective to the original ones of other state-of-the-art methods, we can effectively penalize a geometric inconsistency and obtain a highly accurate depth estimation. Our proposed method is evaluated on the Eigen split of the KITTI raw dataset.

Causal Patterns: Extraction of multiple causal relationships by Mixture of Probabilistic Partial Canonical Correlation Analysis

In this paper, we propose a mixture of probabilistic partial canonical correlation analysis (MPPCCA) that extracts the Causal Patterns from two multivariate time series. Causal patterns refer to the signal patterns within interactions of two elements having multiple types of mutually causal relationships, rather than a mixture of simultaneous correlations or the absence of presence of a causal relationship between the elements. In multivariate statistics, partial canonical correlation analysis (PCCA) evaluates the correlation between two multivariates after subtracting the effect of the third multivariate. PCCA can calculate the Granger Causal- ity Index (which tests whether a time-series can be predicted from an- other time-series), but is not applicable to data containing multiple partial canonical correlations. After introducing the MPPCCA, we propose an expectation-maxmization (EM) algorithm that estimates the parameters and latent variables of the MPPCCA. The MPPCCA is expected to ex- tract multiple partial canonical correlations from data series without any supervised signals to split the data as clusters. The method was then eval- uated in synthetic data experiments. In the synthetic dataset, our method estimated the multiple partial canonical correlations more accurately than the existing method. To determine the types of patterns detectable by the method, experiments were also conducted on real datasets. The method estimated the communication patterns In motion-capture data. The MP- PCCA is applicable to various type of signals such as brain signals, human communication and nonlinear complex multibody systems.