CT-OT Flow: Estimating Continuous-Time Dynamics from Discrete Temporal Snapshots

In many real-world scenarios, such as single-cell RNA sequencing, data are observed only as discrete-time snapshots spanning finite time intervals and subject to noisy timestamps, with no continuous trajectories available. Recovering the underlying continuous-time dynamics from these snapshots with coarse and noisy observation times is a critical and challenging task. We propose Continuous-Time Optimal Transport Flow (CT-OT Flow), which first infers high-resolution time labels via partial optimal transport and then reconstructs a continuous-time data distribution through a temporal kernel smoothing. This reconstruction enables accurate training of dynamics models such as ODEs and SDEs. CT-OT Flow consistently outperforms state-of-the-art methods on synthetic benchmarks and achieves lower reconstruction errors on real scRNA-seq and typhoon-track datasets. Our results highlight the benefits of explicitly modeling temporal discretization and timestamp uncertainty, offering an accurate and general framework for bridging discrete snapshots and continuous-time processes.

An Asymptotic Equation Linking WAIC and WBIC in Singular Models

In statistical learning, models are classified as regular or singular depending on whether the mapping from parameters to probability distributions is injective. Most models with hierarchical structures or latent variables are singular, for which conventional criteria such as the Akaike Information Criterion and the Bayesian Information Criterion are inapplicable due to the breakdown of normal approximations for the likelihood and posterior. To address this, the Widely Applicable Information Criterion (WAIC) and the Widely Applicable Bayesian Information Criterion (WBIC) have been proposed. Since WAIC and WBIC are computed using posterior distributions at different temperature settings, separate posterior sampling is generally required. In this paper, we theoretically derive an asymptotic equation that links WAIC and WBIC, despite their dependence on different posteriors. This equation yields an asymptotically unbiased expression of WAIC in terms of the posterior distribution used for WBIC. The result clarifies the structural relationship between these criteria within the framework of singular learning theory, and deepens understanding of their asymptotic behavior. This theoretical contribution provides a foundation for future developments in the computational efficiency of model selection in singular models.

Upper Bound of Bayesian Generalization Error in Partial Concept Bottleneck Model (CBM): Partial CBM outperforms naive CBM

Concept Bottleneck Model (CBM) is a methods for explaining neural networks. In CBM, concepts which correspond to reasons of outputs are inserted in the last intermediate layer as observed values. It is expected that we can interpret the relationship between the output and concept similar to linear regression. However, this interpretation requires observing all concepts and decreases the generalization performance of neural networks. Partial CBM (PCBM), which uses partially observed concepts, has been devised to resolve these difficulties. Although some numerical experiments suggest that the generalization performance of PCBMs is almost as high as that of the original neural networks, the theoretical behavior of its generalization error has not been yet clarified since PCBM is singular statistical model. In this paper, we reveal the Bayesian generalization error in PCBM with a three-layered and linear architecture. The result indcates that the structure of partially observed concepts decreases the Bayesian generalization error compared with that of CBM (full-observed concepts).

Bayesian Generalization Error in Linear Neural Networks with Concept Bottleneck Structure and Multitask Formulation

Concept bottleneck model (CBM) is a ubiquitous method that can interpret neural networks using concepts. In CBM, concepts are inserted between the output layer and the last intermediate layer as observable values. This helps in understanding the reason behind the outputs generated by the neural networks: the weights corresponding to the concepts from the last hidden layer to the output layer. However, it has not yet been possible to understand the behavior of the generalization error in CBM since a neural network is a singular statistical model in general. When the model is singular, a one to one map from the parameters to probability distributions cannot be created. This non-identifiability makes it difficult to analyze the generalization performance. In this study, we mathematically clarify the Bayesian generalization error and free energy of CBM when its architecture is three-layered linear neural networks. We also consider a multitask problem where the neural network outputs not only the original output but also the concepts. The results show that CBM drastically changes the behavior of the parameter region and the Bayesian generalization error in three-layered linear neural networks as compared with the standard version, whereas the multitask formulation does not.

The Exact Asymptotic Form of Bayesian Generalization Error in Latent Dirichlet Allocation

Latent Dirichlet allocation (LDA) obtains essential information from data by using Bayesian inference. It is applied to knowledge discovery via dimension reducing and clustering in many fields. However, its generalization error had not been yet clarified since it is a singular statistical model where there is no one to one map from parameters to probability distributions. In this paper, we give the exact asymptotic form of its generalization error and marginal likelihood, by theoretical analysis of its learning coefficient using algebraic geometry. The theoretical result shows that the Bayesian generalization error in LDA is expressed in terms of that in matrix factorization and a penalty from the simplex restriction of LDA's parameter region.

Variational Approximation Accuracy in Bayesian Non-negative Matrix Factorization

Non-negative matrix factorization (NMF) is a knowledge discovery method that is used for many fields, besides, its variational inference and Gibbs sampling method are also well-known. However, the variational approximation accuracy is not yet clarified, since NMF is not statistically regular and the prior used in the variational Bayesian NMF (VBNMF) has zero or divergence points. In this paper, using algebraic geometrical methods, we theoretically analyze the difference of the negative log evidence/marginal likelihood (free energy) between VBNMF and Bayesian NMF, and give a lower bound of the approximation accuracy, asymptotically. The results quantitatively show how well the VBNMF algorithm can approximate Bayesian NMF.

Asymptotic Bayesian Generalization Error in a General Stochastic Matrix Factorization

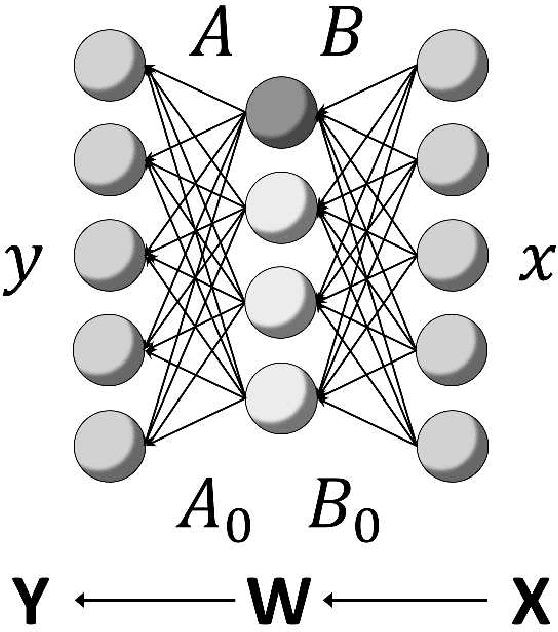
Stochastic matrix factorization (SMF) can be regarded as a restriction of non-negative matrix factorization (NMF). SMF is useful for inference of topic models, NMF for binary matrices data, Markov chains, and Bayesian networks. However, SMF needs strong assumptions to reach a unique factorization and its theoretical prediction accuracy has not yet been clarified. In this paper, we study the maximum the pole of zeta function (real log canonical threshold) of a general SMF and derive an upper bound of the generalization error in Bayesian inference. The results give a foundation for a widely applicable and rigorous factorization method of SMF and mean that the generalization error in SMF becomes smaller than regular statistical models by Bayesian inference.

Upper Bound of Bayesian Generalization Error in Non-negative Matrix Factorization

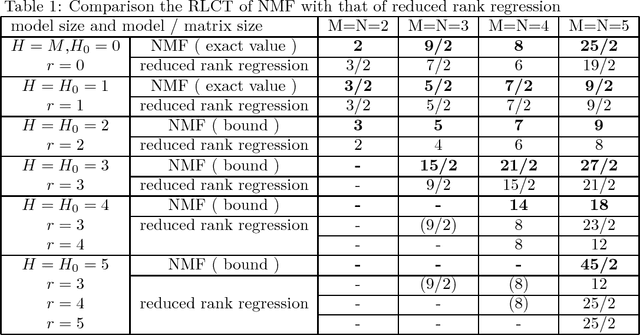
Non-negative matrix factorization (NMF) is a new knowledge discovery method that is used for text mining, signal processing, bioinformatics, and consumer analysis. However, its basic property as a learning machine is not yet clarified, as it is not a regular statistical model, resulting that theoretical optimization method of NMF has not yet established. In this paper, we study the real log canonical threshold of NMF and give an upper bound of the generalization error in Bayesian learning. The results show that the generalization error of the matrix factorization can be made smaller than regular statistical models if Bayesian learning is applied.