Asymptotic Bayesian Generalization Error in a General Stochastic Matrix Factorization

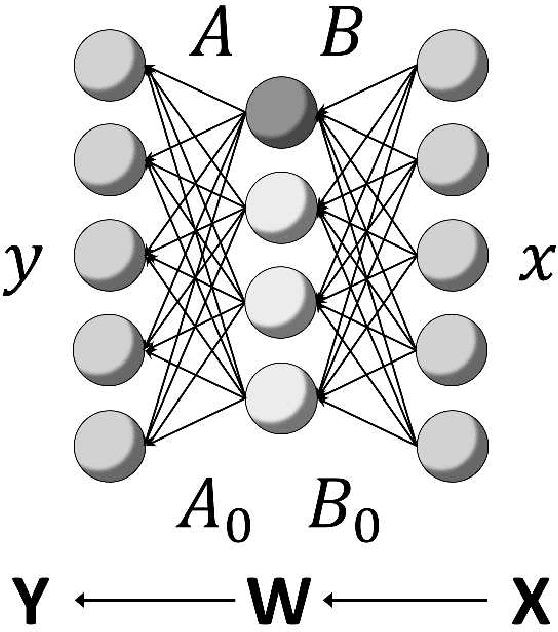
Stochastic matrix factorization (SMF) can be regarded as a restriction of non-negative matrix factorization (NMF). SMF is useful for inference of topic models, NMF for binary matrices data, Markov chains, and Bayesian networks. However, SMF needs strong assumptions to reach a unique factorization and its theoretical prediction accuracy has not yet been clarified. In this paper, we study the maximum the pole of zeta function (real log canonical threshold) of a general SMF and derive an upper bound of the generalization error in Bayesian inference. The results give a foundation for a widely applicable and rigorous factorization method of SMF and mean that the generalization error in SMF becomes smaller than regular statistical models by Bayesian inference.