Free energy of Bayesian Convolutional Neural Network with Skip Connection

Since the success of Residual Network(ResNet), many of architectures of Convolutional Neural Networks(CNNs) have adopted skip connection. While the generalization performance of CNN with skip connection has been explained within the framework of Ensemble Learning, the dependency on the number of parameters have not been revealed. In this paper, we show that Bayesian free energy of Convolutional Neural Network both with and without skip connection in Bayesian learning. The upper bound of free energy of Bayesian CNN with skip connection does not depend on the oveparametrization and, the generalization error of Bayesian CNN has similar property.

Bayesian Free Energy of Deep ReLU Neural Network in Overparametrized Cases

In many research fields in artificial intelligence, it has been shown that deep neural networks are useful to estimate unknown functions on high dimensional input spaces. However, their generalization performance is not yet completely clarified from the theoretical point of view because they are nonidentifiable and singular learning machines. Moreover, a ReLU function is not differentiable, to which algebraic or analytic methods in singular learning theory cannot be applied. In this paper, we study a deep ReLU neural network in overparametrized cases and prove that the Bayesian free energy, which is equal to the minus log marginal likelihoodor the Bayesian stochastic complexity, is bounded even if the number of layers are larger than necessary to estimate an unknown data-generating function. Since the Bayesian generalization error is equal to the increase of the free energy as a function of a sample size, our result also shows that the Bayesian generalization error does not increase even if a deep ReLU neural network is designed to be sufficiently large or in an opeverparametrized state.

Upper Bound of Real Log Canonical Threshold of Tensor Decomposition and its Application to Bayesian Inference

Tensor decomposition is now being used for data analysis, information compression, and knowledge recovery. However, the mathematical property of tensor decomposition is not yet fully clarified because it is one of singular learning machines. In this paper, we give the upper bound of its real log canonical threshold (RLCT) of the tensor decomposition by using an algebraic geometrical method and derive its Bayesian generalization error theoretically. We also give considerations about its mathematical property through numerical experiments.

Recent Advances in Algebraic Geometry and Bayesian Statistics

This article is a review of theoretical advances in the research field of algebraic geometry and Bayesian statistics in the last two decades. Many statistical models and learning machines which contain hierarchical structures or latent variables are called nonidentifiable, because the map from a parameter to a statistical model is not one-to-one. In nonidentifiable models, both the likelihood function and the posterior distribution have singularities in general, hence it was difficult to analyze their statistical properties. However, from the end of the 20th century, new theory and methodology based on algebraic geometry have been established which enables us to investigate such models and machines in the real world. In this article, the following results in recent advances are reported. First, we explain the framework of Bayesian statistics and introduce a new perspective from the birational geometry. Second, two mathematical solutions are derived based on algebraic geometry. An appropriate parameter space can be found by a resolution map, which makes the posterior distribution be normal crossing and the log likelihood ratio function be well-defined. Third, three applications to statistics are introduced. The posterior distribution is represented by the renormalized form, the asymptotic free energy is derived, and the universal formula among the generalization loss, the cross validation, and the information criterion is established. Two mathematical solutions and three applications to statistics based on algebraic geometry reported in this article are now being used in many practical fields in data science and artificial intelligence.

Mathematical Theory of Bayesian Statistics for Unknown Information Source

In statistical inference, uncertainty is unknown and all models are wrong. A person who makes a statistical model and a prior distribution is simultaneously aware that they are fictional and virtual candidates. In order to study such cases, several statistical measures have been constructed, such as cross validation, information criteria, and marginal likelihood, however, their mathematical properties have not yet been completely clarified when statistical models are under- and over- parametrized. In this paper, we introduce a place of mathematical theory of Bayesian statistics for unknown uncertainty, on which we show general properties of cross validation, information criteria, and marginal likelihood. The derived theory holds even if an unknown uncertainty is unrealizable by a statistical model or even if the posterior distribution cannot be approximated by any normal distribution, hence it gives a helpful standpoint for a person who cannot believe in any specific model and prior. The results are followings. (1) There exists a more precise statistical measure of the generalization loss than leave-one-out cross validation and information criterion based on the mathematical properties of them. (2) There exists a more efficient approximation method of the free energy, which is the minus log marginal likelihood, even if the posterior distribution cannot be approximated by any normal distribution. (3) And the prior distributions optimized by the cross validation and the widely applicable information criterion are asymptotically equivalent to each other, which are different from that by the marginal likelihood.

Asymptotic Behavior of Bayesian Generalization Error in Multinomial Mixtures

Multinomial mixtures are widely used in the information engineering field, however, their mathematical properties are not yet clarified because they are singular learning models. In fact, the models are non-identifiable and their Fisher information matrices are not positive definite. In recent years, the mathematical foundation of singular statistical models are clarified by using algebraic geometric methods. In this paper, we clarify the real log canonical thresholds and multiplicities of the multinomial mixtures and elucidate their asymptotic behaviors of generalization error and free energy.

Asymptotic Bayesian Generalization Error in a General Stochastic Matrix Factorization

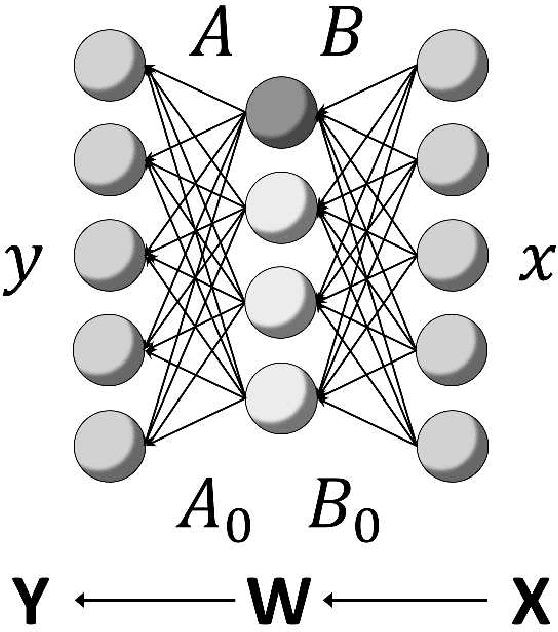
Stochastic matrix factorization (SMF) can be regarded as a restriction of non-negative matrix factorization (NMF). SMF is useful for inference of topic models, NMF for binary matrices data, Markov chains, and Bayesian networks. However, SMF needs strong assumptions to reach a unique factorization and its theoretical prediction accuracy has not yet been clarified. In this paper, we study the maximum the pole of zeta function (real log canonical threshold) of a general SMF and derive an upper bound of the generalization error in Bayesian inference. The results give a foundation for a widely applicable and rigorous factorization method of SMF and mean that the generalization error in SMF becomes smaller than regular statistical models by Bayesian inference.

Upper Bound of Bayesian Generalization Error in Non-negative Matrix Factorization

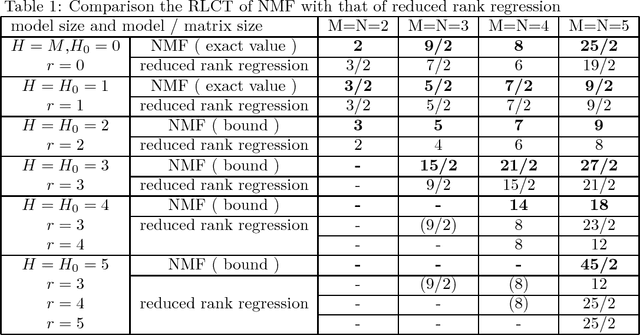
Non-negative matrix factorization (NMF) is a new knowledge discovery method that is used for text mining, signal processing, bioinformatics, and consumer analysis. However, its basic property as a learning machine is not yet clarified, as it is not a regular statistical model, resulting that theoretical optimization method of NMF has not yet established. In this paper, we study the real log canonical threshold of NMF and give an upper bound of the generalization error in Bayesian learning. The results show that the generalization error of the matrix factorization can be made smaller than regular statistical models if Bayesian learning is applied.

Bayesian Cross Validation and WAIC for Predictive Prior Design in Regular Asymptotic Theory

Prior design is one of the most important problems in both statistics and machine learning. The cross validation (CV) and the widely applicable information criterion (WAIC) are predictive measures of the Bayesian estimation, however, it has been difficult to apply them to find the optimal prior because their mathematical properties in prior evaluation have been unknown and the region of the hyperparameters is too wide to be examined. In this paper, we derive a new formula by which the theoretical relation among CV, WAIC, and the generalization loss is clarified and the optimal hyperparameter can be directly found. By the formula, three facts are clarified about predictive prior design. Firstly, CV and WAIC have the same second order asymptotic expansion, hence they are asymptotically equivalent to each other as the optimizer of the hyperparameter. Secondly, the hyperparameter which minimizes CV or WAIC makes the average generalization loss to be minimized asymptotically but does not the random generalization loss. And lastly, by using the mathematical relation between priors, the variances of the optimized hyperparameters by CV and WAIC are made smaller with small computational costs. Also we show that the optimized hyperparameter by DIC or the marginal likelihood does not minimize the average or random generalization loss in general.

A Widely Applicable Bayesian Information Criterion

A statistical model or a learning machine is called regular if the map taking a parameter to a probability distribution is one-to-one and if its Fisher information matrix is always positive definite. If otherwise, it is called singular. In regular statistical models, the Bayes free energy, which is defined by the minus logarithm of Bayes marginal likelihood, can be asymptotically approximated by the Schwarz Bayes information criterion (BIC), whereas in singular models such approximation does not hold. Recently, it was proved that the Bayes free energy of a singular model is asymptotically given by a generalized formula using a birational invariant, the real log canonical threshold (RLCT), instead of half the number of parameters in BIC. Theoretical values of RLCTs in several statistical models are now being discovered based on algebraic geometrical methodology. However, it has been difficult to estimate the Bayes free energy using only training samples, because an RLCT depends on an unknown true distribution. In the present paper, we define a widely applicable Bayesian information criterion (WBIC) by the average log likelihood function over the posterior distribution with the inverse temperature $1/\log n$, where $n$ is the number of training samples. We mathematically prove that WBIC has the same asymptotic expansion as the Bayes free energy, even if a statistical model is singular for and unrealizable by a statistical model. Since WBIC can be numerically calculated without any information about a true distribution, it is a generalized version of BIC onto singular statistical models.