Free energy of Bayesian Convolutional Neural Network with Skip Connection

Since the success of Residual Network(ResNet), many of architectures of Convolutional Neural Networks(CNNs) have adopted skip connection. While the generalization performance of CNN with skip connection has been explained within the framework of Ensemble Learning, the dependency on the number of parameters have not been revealed. In this paper, we show that Bayesian free energy of Convolutional Neural Network both with and without skip connection in Bayesian learning. The upper bound of free energy of Bayesian CNN with skip connection does not depend on the oveparametrization and, the generalization error of Bayesian CNN has similar property.

Bayesian Free Energy of Deep ReLU Neural Network in Overparametrized Cases

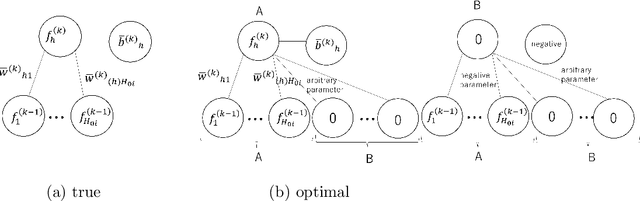
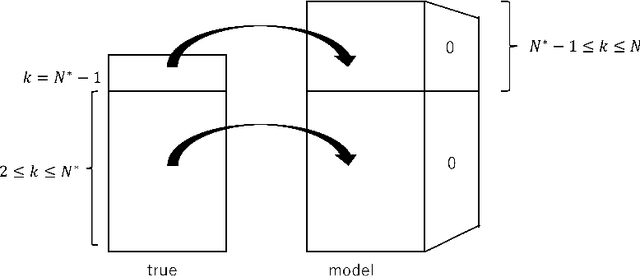
In many research fields in artificial intelligence, it has been shown that deep neural networks are useful to estimate unknown functions on high dimensional input spaces. However, their generalization performance is not yet completely clarified from the theoretical point of view because they are nonidentifiable and singular learning machines. Moreover, a ReLU function is not differentiable, to which algebraic or analytic methods in singular learning theory cannot be applied. In this paper, we study a deep ReLU neural network in overparametrized cases and prove that the Bayesian free energy, which is equal to the minus log marginal likelihoodor the Bayesian stochastic complexity, is bounded even if the number of layers are larger than necessary to estimate an unknown data-generating function. Since the Bayesian generalization error is equal to the increase of the free energy as a function of a sample size, our result also shows that the Bayesian generalization error does not increase even if a deep ReLU neural network is designed to be sufficiently large or in an opeverparametrized state.