Effect of Random Learning Rate: Theoretical Analysis of SGD Dynamics in Non-Convex Optimization via Stationary Distribution

We consider a variant of the stochastic gradient descent (SGD) with a random learning rate and reveal its convergence properties. SGD is a widely used stochastic optimization algorithm in machine learning, especially deep learning. Numerous studies reveal the convergence properties of SGD and its simplified variants. Among these, the analysis of convergence using a stationary distribution of updated parameters provides generalizable results. However, to obtain a stationary distribution, the update direction of the parameters must not degenerate, which limits the applicable variants of SGD. In this study, we consider a novel SGD variant, Poisson SGD, which has degenerated parameter update directions and instead utilizes a random learning rate. Consequently, we demonstrate that a distribution of a parameter updated by Poisson SGD converges to a stationary distribution under weak assumptions on a loss function. Based on this, we further show that Poisson SGD finds global minima in non-convex optimization problems and also evaluate the generalization error using this method. As a proof technique, we approximate the distribution by Poisson SGD with that of the bouncy particle sampler (BPS) and derive its stationary distribution, using the theoretical advance of the piece-wise deterministic Markov process (PDMP).

Upper Bound of Real Log Canonical Threshold of Tensor Decomposition and its Application to Bayesian Inference

Tensor decomposition is now being used for data analysis, information compression, and knowledge recovery. However, the mathematical property of tensor decomposition is not yet fully clarified because it is one of singular learning machines. In this paper, we give the upper bound of its real log canonical threshold (RLCT) of the tensor decomposition by using an algebraic geometrical method and derive its Bayesian generalization error theoretically. We also give considerations about its mathematical property through numerical experiments.

Decoding Cosmological Information in Weak-Lensing Mass Maps with Generative Adversarial Networks

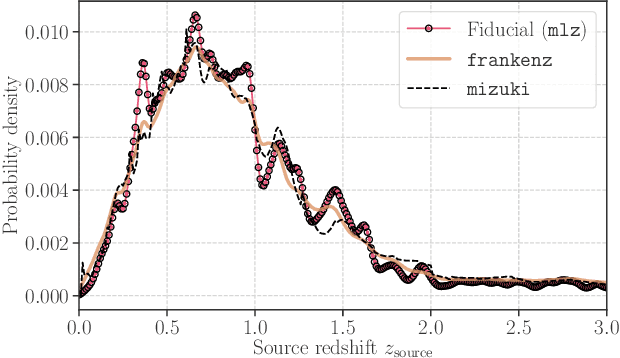
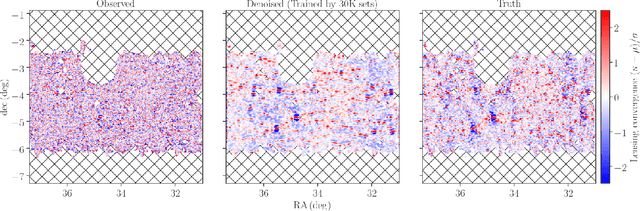
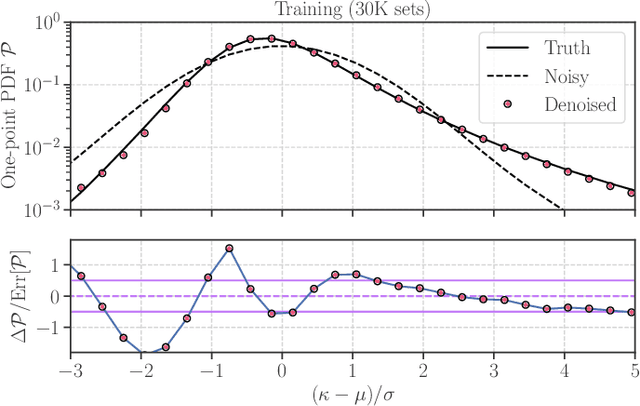
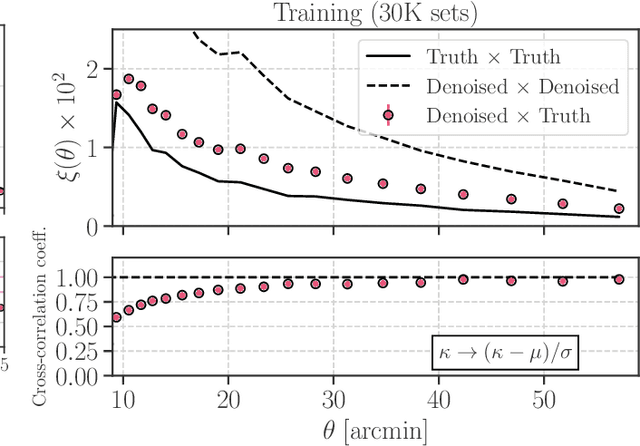
Galaxy imaging surveys enable us to map the cosmic matter density field through weak gravitational lensing analysis. The density reconstruction is compromised by a variety of noise originating from observational conditions, galaxy number density fluctuations, and intrinsic galaxy properties. We propose a deep-learning approach based on generative adversarial networks (GANs) to reduce the noise in the weak lensing map under realistic conditions. We perform image-to-image translation using conditional GANs in order to produce noiseless lensing maps using the first-year data of the Subaru Hyper Suprime-Cam (HSC) survey. We train the conditional GANs by using 30000 sets of mock HSC catalogs that directly incorporate observational effects. We show that an ensemble learning method with GANs can reproduce the one-point probability distribution function (PDF) of the lensing convergence map within a $0.5-1\sigma$ level. We use the reconstructed PDFs to estimate a cosmological parameter $S_{8} = \sigma_{8}\sqrt{\Omega_{\rm m0}/0.3}$, where $\Omega_{\rm m0}$ and $\sigma_{8}$ represent the mean and the scatter in the cosmic matter density. The reconstructed PDFs place tighter constraint, with the statistical uncertainty in $S_8$ reduced by a factor of $2$ compared to the noisy PDF. This is equivalent to increasing the survey area by $4$ without denoising by GANs. Finally, we apply our denoising method to the first-year HSC data, to place $2\sigma$-level cosmological constraints of $S_{8} < 0.777 \, ({\rm stat}) + 0.105 \, ({\rm sys})$ and $S_{8} < 0.633 \, ({\rm stat}) + 0.114 \, ({\rm sys})$ for the noisy and denoised data, respectively.

Denoising Weak Lensing Mass Maps with Deep Learning

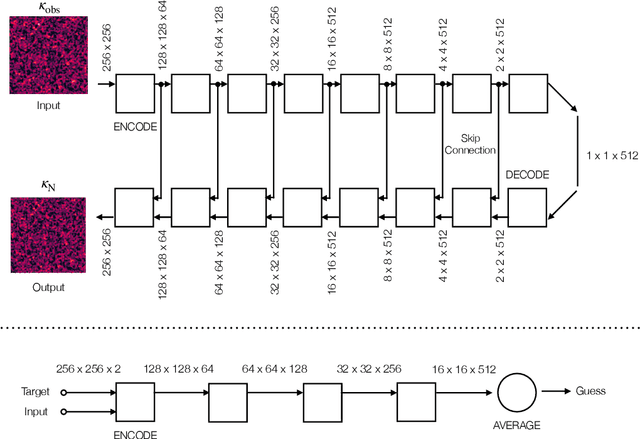
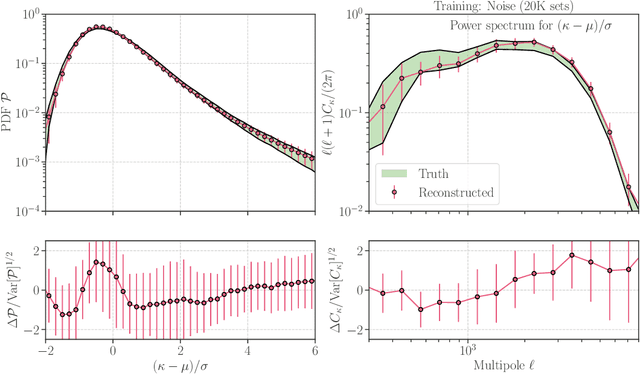
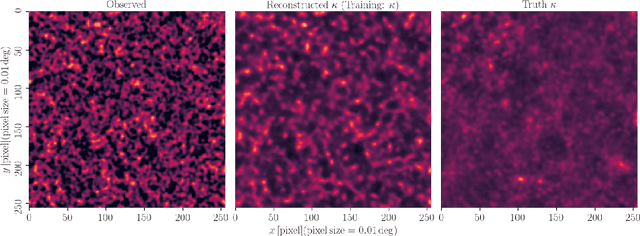
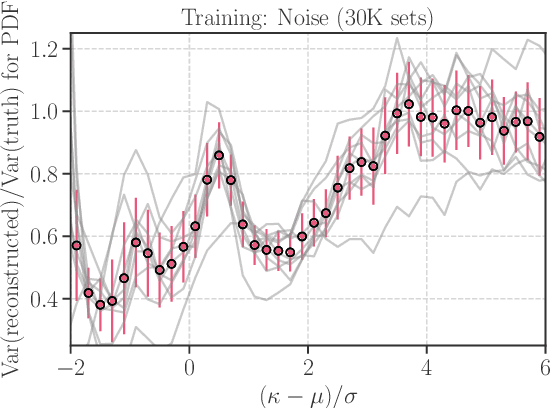
Weak gravitational lensing is a powerful probe of the large-scale cosmic matter distribution. Wide-field galaxy surveys allow us to generate the so-called weak lensing maps, but actual observations suffer from noise due to imperfect measurement of galaxy shape distortions and to the limited number density of the source galaxies. In this paper, we explore a deep-learning approach to reduce the noise. We develop an image-to-image translation method with conditional adversarial networks (CANs), which learn efficient mapping from an input noisy weak lensing map to the underlying noise field. We train the CANs using 30000 image pairs obtained from 1000 ray-tracing simulations of weak gravitational lensing. We show that the trained CANs reproduce the true one-point probability distribution function of the noiseless lensing map with a bias less than $1\sigma$ on average, where $\sigma$ is the statistical error. Since a number of model parameters are used in our CANs, our method has additional error budgets when reconstructing the summary statistics of weak lensing maps. The typical amplitude of such reconstruction error is found to be of $1-2\sigma$ level. Interestingly, pixel-by-pixel denoising for under-dense regions is less biased than denoising over-dense regions. Our deep-learning approach is complementary to existing analysis methods which focus on clustering properties and peak statistics of weak lensing maps.

Single-epoch supernova classification with deep convolutional neural networks

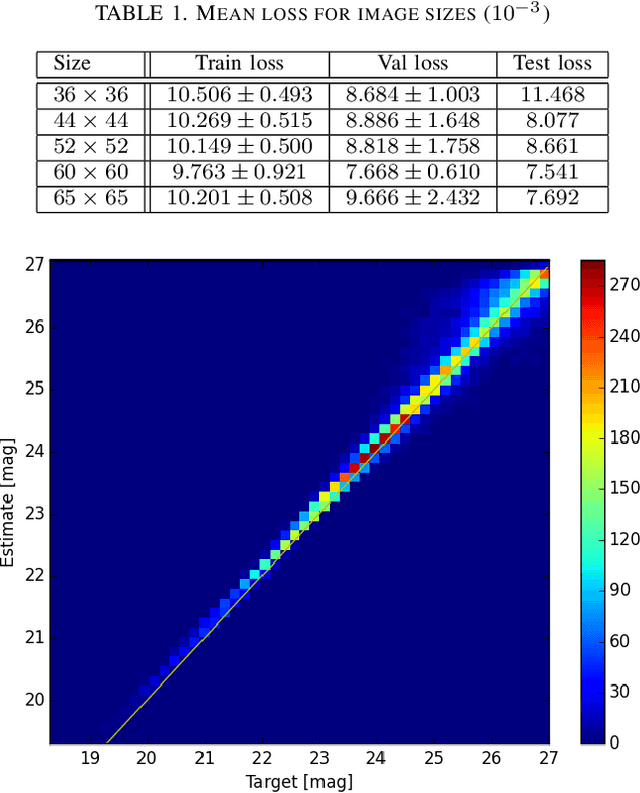
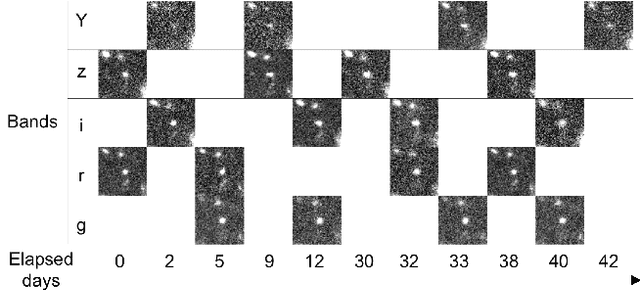
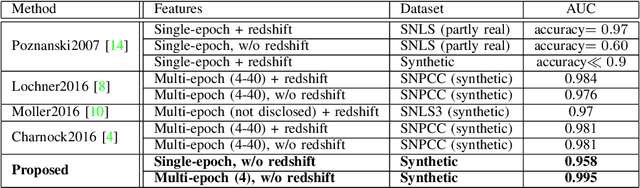
Supernovae Type-Ia (SNeIa) play a significant role in exploring the history of the expansion of the Universe, since they are the best-known standard candles with which we can accurately measure the distance to the objects. Finding large samples of SNeIa and investigating their detailed characteristics have become an important issue in cosmology and astronomy. Existing methods relied on a photometric approach that first measures the luminance of supernova candidates precisely and then fits the results to a parametric function of temporal changes in luminance. However, it inevitably requires multi-epoch observations and complex luminance measurements. In this work, we present a novel method for classifying SNeIa simply from single-epoch observation images without any complex measurements, by effectively integrating the state-of-the-art computer vision methodology into the standard photometric approach. Our method first builds a convolutional neural network for estimating the luminance of supernovae from telescope images, and then constructs another neural network for the classification, where the estimated luminance and observation dates are used as features for classification. Both of the neural networks are integrated into a single deep neural network to classify SNeIa directly from observation images. Experimental results show the effectiveness of the proposed method and reveal classification performance comparable to existing photometric methods with multi-epoch observations.