Blind Deconvolution with Non-smooth Regularization via Bregman Proximal DCAs

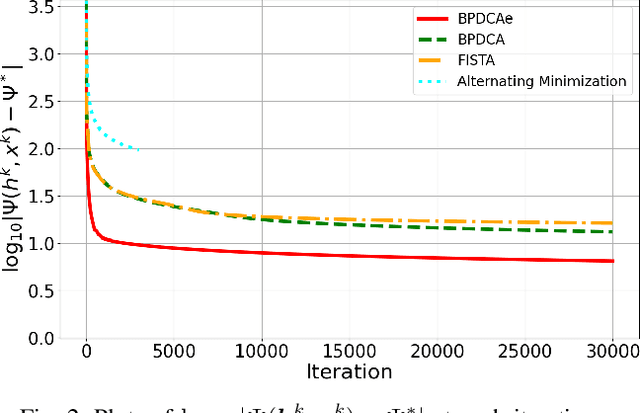
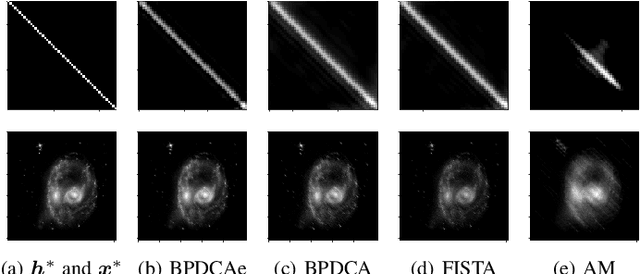
Blind deconvolution is a technique to recover an original signal without knowing a convolving filter. It is naturally formulated as a minimization of a quartic objective function under some assumption. Because its differentiable part does not have a Lipschitz continuous gradient, existing first-order methods are not theoretically supported. In this letter, we employ the Bregman-based proximal methods, whose convergence is theoretically guaranteed under the $L$-smad property. We first reformulate the objective function as a difference of convex (DC) functions and apply the Bregman proximal DC algorithm (BPDCA). This DC decomposition satisfies the $L$-smad property. The method is extended to the BPDCA with extrapolation (BPDCAe) for faster convergence. When our regularizer has a sufficiently simple structure, each iteration is solved in a closed-form expression, and thus our algorithms solve large-scale problems efficiently. We also provide the stability analysis of the equilibriums and demonstrate the proposed methods through numerical experiments on image deblurring. The results show that BPDCAe successfully recovered the original image and outperformed other existing algorithms.

Decoding Cosmological Information in Weak-Lensing Mass Maps with Generative Adversarial Networks

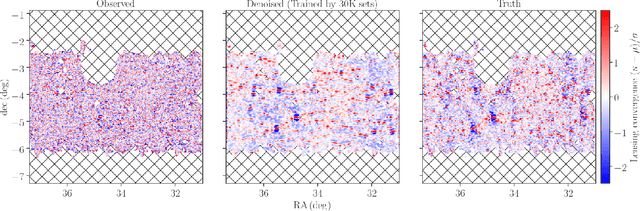
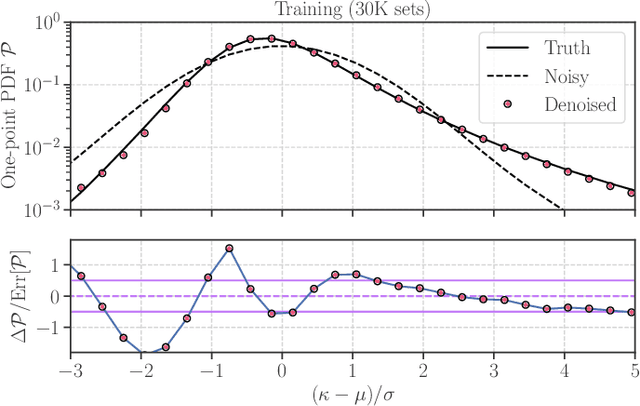
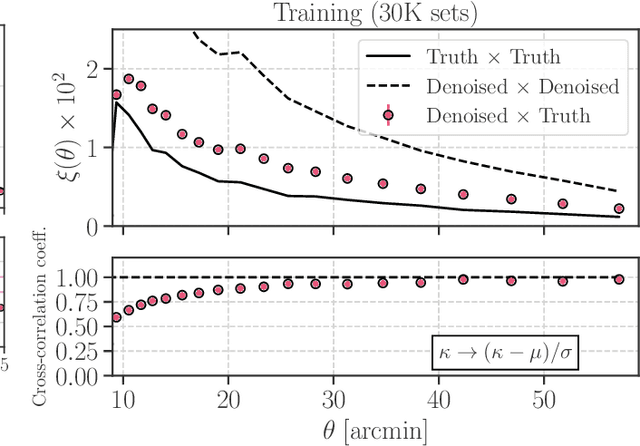
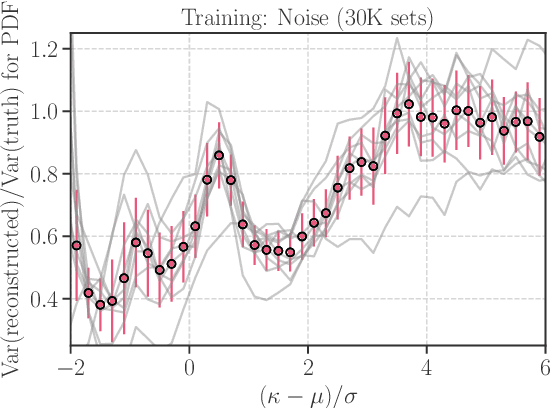
Galaxy imaging surveys enable us to map the cosmic matter density field through weak gravitational lensing analysis. The density reconstruction is compromised by a variety of noise originating from observational conditions, galaxy number density fluctuations, and intrinsic galaxy properties. We propose a deep-learning approach based on generative adversarial networks (GANs) to reduce the noise in the weak lensing map under realistic conditions. We perform image-to-image translation using conditional GANs in order to produce noiseless lensing maps using the first-year data of the Subaru Hyper Suprime-Cam (HSC) survey. We train the conditional GANs by using 30000 sets of mock HSC catalogs that directly incorporate observational effects. We show that an ensemble learning method with GANs can reproduce the one-point probability distribution function (PDF) of the lensing convergence map within a $0.5-1\sigma$ level. We use the reconstructed PDFs to estimate a cosmological parameter $S_{8} = \sigma_{8}\sqrt{\Omega_{\rm m0}/0.3}$, where $\Omega_{\rm m0}$ and $\sigma_{8}$ represent the mean and the scatter in the cosmic matter density. The reconstructed PDFs place tighter constraint, with the statistical uncertainty in $S_8$ reduced by a factor of $2$ compared to the noisy PDF. This is equivalent to increasing the survey area by $4$ without denoising by GANs. Finally, we apply our denoising method to the first-year HSC data, to place $2\sigma$-level cosmological constraints of $S_{8} < 0.777 \, ({\rm stat}) + 0.105 \, ({\rm sys})$ and $S_{8} < 0.633 \, ({\rm stat}) + 0.114 \, ({\rm sys})$ for the noisy and denoised data, respectively.

Denoising Weak Lensing Mass Maps with Deep Learning

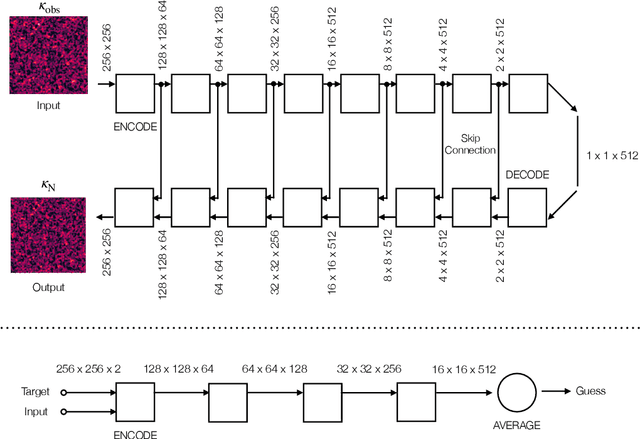
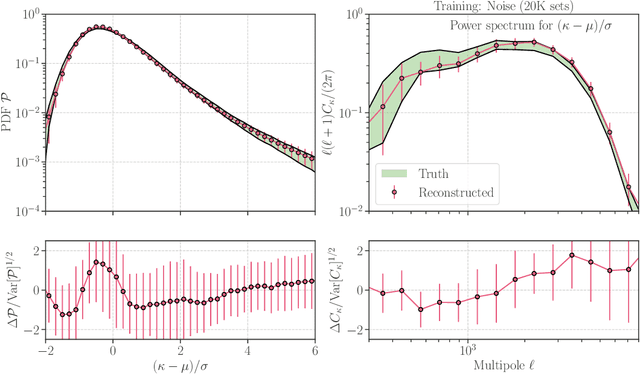
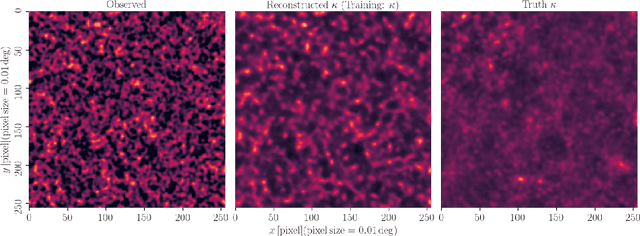
Weak gravitational lensing is a powerful probe of the large-scale cosmic matter distribution. Wide-field galaxy surveys allow us to generate the so-called weak lensing maps, but actual observations suffer from noise due to imperfect measurement of galaxy shape distortions and to the limited number density of the source galaxies. In this paper, we explore a deep-learning approach to reduce the noise. We develop an image-to-image translation method with conditional adversarial networks (CANs), which learn efficient mapping from an input noisy weak lensing map to the underlying noise field. We train the CANs using 30000 image pairs obtained from 1000 ray-tracing simulations of weak gravitational lensing. We show that the trained CANs reproduce the true one-point probability distribution function of the noiseless lensing map with a bias less than $1\sigma$ on average, where $\sigma$ is the statistical error. Since a number of model parameters are used in our CANs, our method has additional error budgets when reconstructing the summary statistics of weak lensing maps. The typical amplitude of such reconstruction error is found to be of $1-2\sigma$ level. Interestingly, pixel-by-pixel denoising for under-dense regions is less biased than denoising over-dense regions. Our deep-learning approach is complementary to existing analysis methods which focus on clustering properties and peak statistics of weak lensing maps.

Exhaustive search for sparse variable selection in linear regression

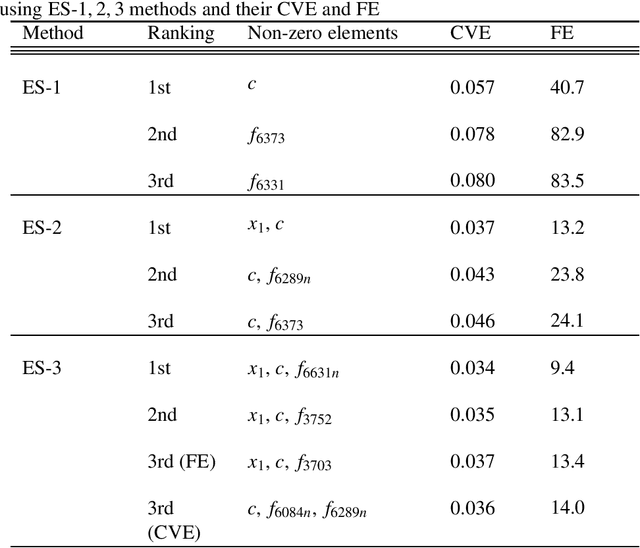
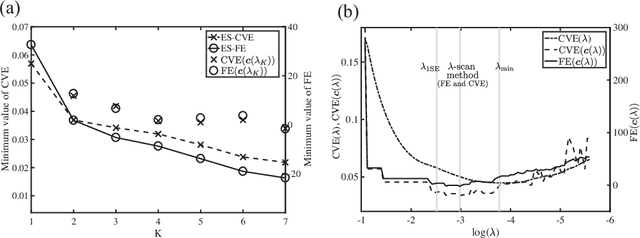
We propose a K-sparse exhaustive search (ES-K) method and a K-sparse approximate exhaustive search method (AES-K) for selecting variables in linear regression. With these methods, K-sparse combinations of variables are tested exhaustively assuming that the optimal combination of explanatory variables is K-sparse. By collecting the results of exhaustively computing ES-K, various approximate methods for selecting sparse variables can be summarized as density of states. With this density of states, we can compare different methods for selecting sparse variables such as relaxation and sampling. For large problems where the combinatorial explosion of explanatory variables is crucial, the AES-K method enables density of states to be effectively reconstructed by using the replica-exchange Monte Carlo method and the multiple histogram method. Applying the ES-K and AES-K methods to type Ia supernova data, we confirmed the conventional understanding in astronomy when an appropriate K is given beforehand. However, we found the difficulty to determine K from the data. Using virtual measurement and analysis, we argue that this is caused by data shortage.