Blind Deconvolution with Non-smooth Regularization via Bregman Proximal DCAs

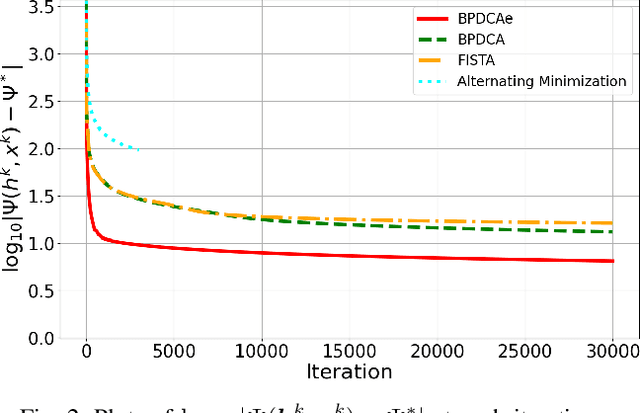
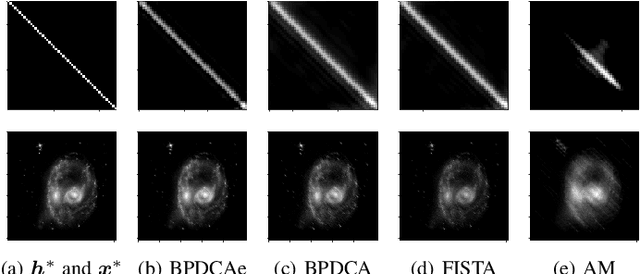
Blind deconvolution is a technique to recover an original signal without knowing a convolving filter. It is naturally formulated as a minimization of a quartic objective function under some assumption. Because its differentiable part does not have a Lipschitz continuous gradient, existing first-order methods are not theoretically supported. In this letter, we employ the Bregman-based proximal methods, whose convergence is theoretically guaranteed under the $L$-smad property. We first reformulate the objective function as a difference of convex (DC) functions and apply the Bregman proximal DC algorithm (BPDCA). This DC decomposition satisfies the $L$-smad property. The method is extended to the BPDCA with extrapolation (BPDCAe) for faster convergence. When our regularizer has a sufficiently simple structure, each iteration is solved in a closed-form expression, and thus our algorithms solve large-scale problems efficiently. We also provide the stability analysis of the equilibriums and demonstrate the proposed methods through numerical experiments on image deblurring. The results show that BPDCAe successfully recovered the original image and outperformed other existing algorithms.

A Gradient Method for Multilevel Optimization

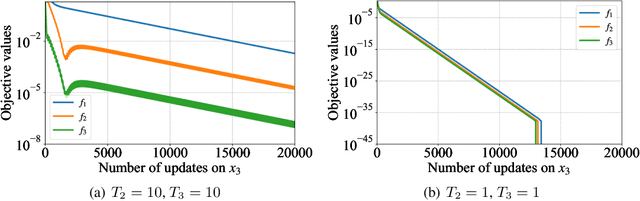
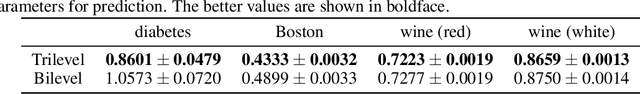
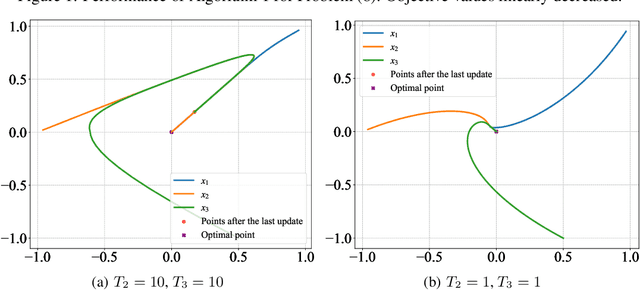
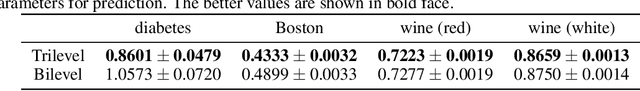
Although application examples of multilevel optimization have already been discussed since the '90s, the development of solution methods was almost limited to bilevel cases due to the difficulty of the problem. In recent years, in machine learning, Franceschi et al. have proposed a method for solving bilevel optimization problems by replacing their lower-level problems with the $T$ steepest descent update equations with some prechosen iteration number $T$. In this paper, we have developed a gradient-based algorithm for multilevel optimization with $n$ levels based on their idea and proved that our reformulation with $n T$ variables asymptotically converges to the original multilevel problem. As far as we know, this is one of the first algorithms with some theoretical guarantee for multilevel optimization. Numerical experiments show that a trilevel hyperparameter learning model considering data poisoning produces more stable prediction results than an existing bilevel hyperparameter learning model in noisy data settings.

Semi-flat minima and saddle points by embedding neural networks to overparameterization

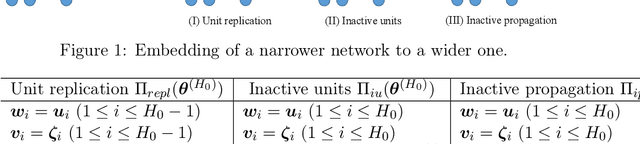
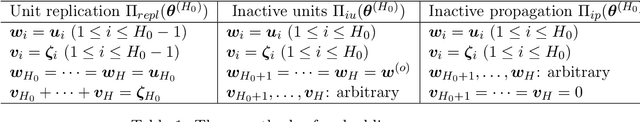
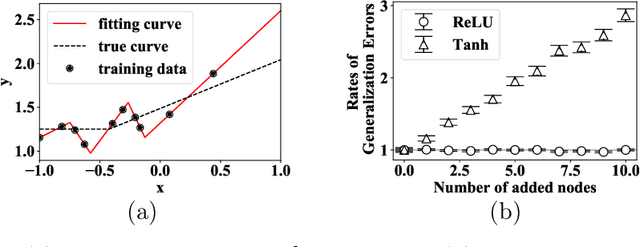
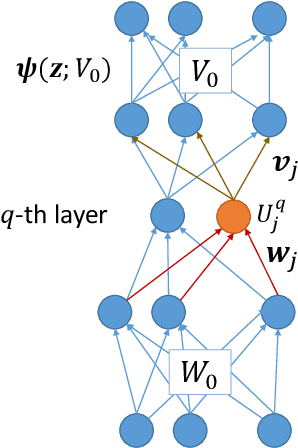
We theoretically study the landscape of the training error for neural networks in overparameterized cases. We consider three basic methods for embedding a network into a wider one with more hidden units, and discuss whether a minimum point of the narrower network gives a minimum or saddle point of the wider one. Our results show that the networks with smooth and ReLU activation have different partially flat landscapes around the embedded point. We also relate these results to a difference of their generalization abilities in overparameterized realization.

Efficient Preconditioning for Noisy Separable NMFs by Successive Projection Based Low-Rank Approximations

The successive projection algorithm (SPA) can quickly solve a nonnegative matrix factorization problem under a separability assumption. Even if noise is added to the problem, SPA is robust as long as the perturbations caused by the noise are small. In particular, robustness against noise should be high when handling the problems arising from real applications. The preconditioner proposed by Gillis and Vavasis (2015) makes it possible to enhance the noise robustness of SPA. Meanwhile, an additional computational cost is required. The construction of the preconditioner contains a step to compute the top-$k$ truncated singular value decomposition of an input matrix. It is known that the decomposition provides the best rank-$k$ approximation to the input matrix; in other words, a matrix with the smallest approximation error among all matrices of rank less than $k$. This step is an obstacle to an efficient implementation of the preconditioned SPA. To address the cost issue, we propose a modification of the algorithm for constructing the preconditioner. Although the original algorithm uses the best rank-$k$ approximation, instead of it, our modification uses an alternative. Ideally, this alternative should have high approximation accuracy and low computational cost. To ensure this, our modification employs a rank-$k$ approximation produced by an SPA based algorithm. We analyze the accuracy of the approximation and evaluate the computational cost of the algorithm. We then present an empirical study revealing the actual performance of the SPA based rank-$k$ approximation algorithm and the modified preconditioned SPA.