Algebraic Geometrical Analysis of Metropolis Algorithm When Parameters Are Non-identifiable

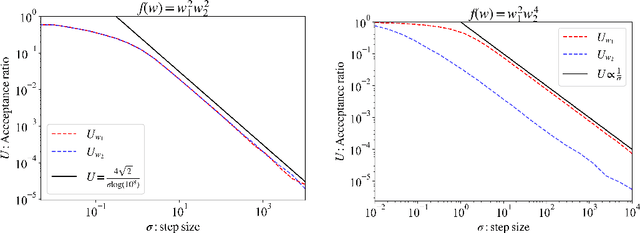
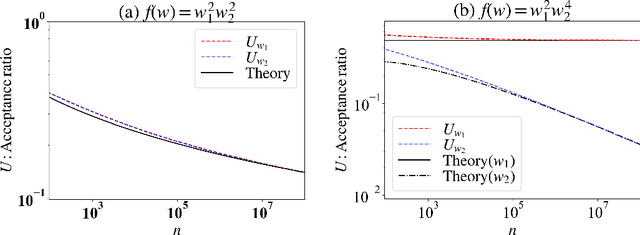
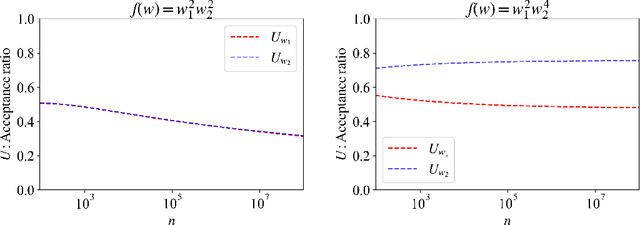
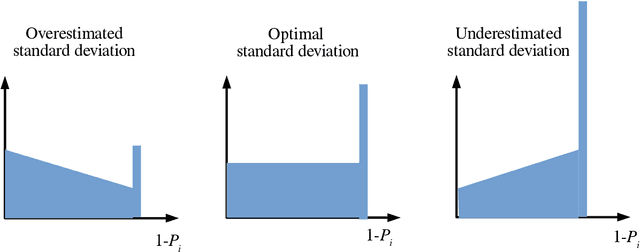
The Metropolis algorithm is one of the Markov chain Monte Carlo (MCMC) methods that realize sampling from the target probability distribution. In this paper, we are concerned with the sampling from the distribution in non-identifiable cases that involve models with Fisher information matrices that may fail to be invertible. The theoretical adjustment of the step size, which is the variance of the candidate distribution, is difficult for non-identifiable cases. In this study, to establish such a principle, the average acceptance rate, which is used as a guideline to optimize the step size in the MCMC method, was analytically derived in non-identifiable cases. The optimization principle for the step size was developed from the viewpoint of the average acceptance rate. In addition, we performed numerical experiments on some specific target distributions to verify the effectiveness of our theoretical results.

Forecasting of the development of a partially-observed dynamical time series with the aid of time-invariance and linearity

A dynamical system produces a dependent multivariate sequence called dynamical time series, developed with an evolution function. As variables in the dynamical time series at the current time-point usually depend on the whole variables in the previous time-point, existing studies forecast the variables at the future time-point by estimating the evolution function. However, some variables in the dynamical time-series are missing in some practical situations. In this study, we propose an autoregressive with slack time series (ARS) model. ARS model involves the simultaneous estimation of the evolution function and the underlying missing variables as a slack time series, with the aid of the time-invariance and linearity of the dynamical system. This study empirically demonstrates the effectiveness of the proposed ARS model.

Signal identification without signal formulation

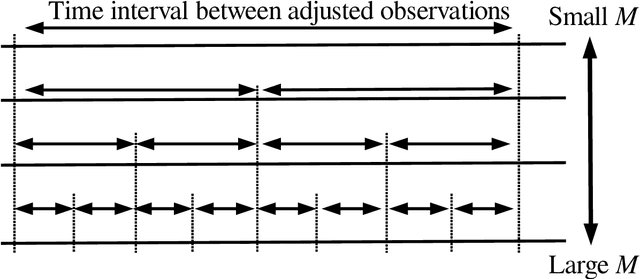
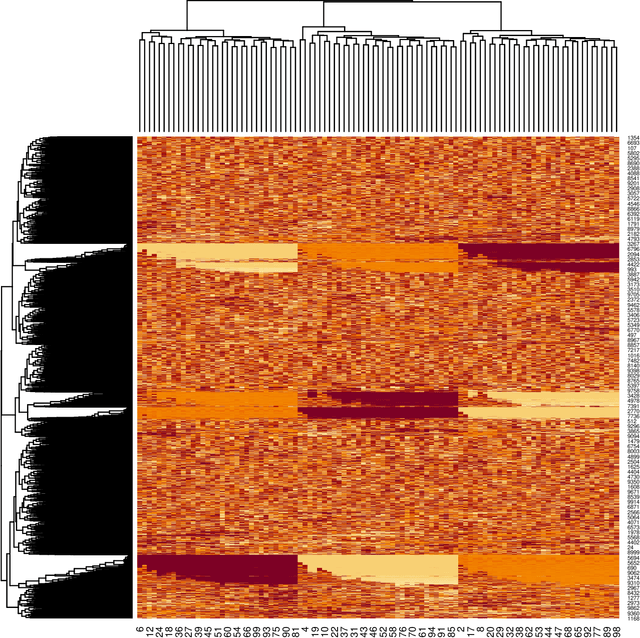
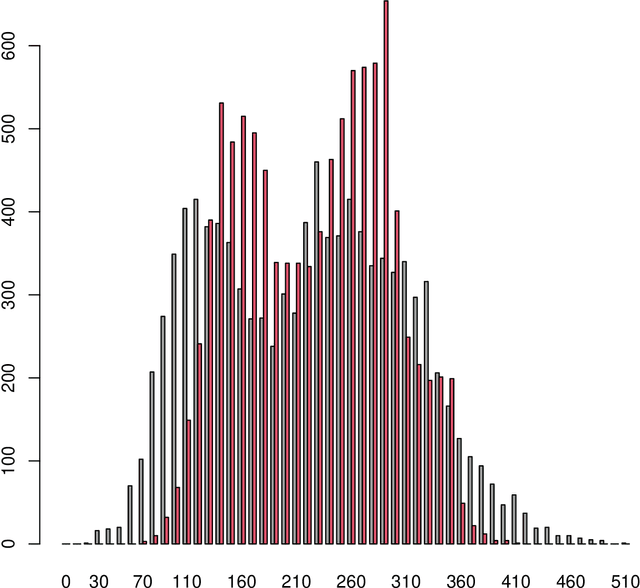
When there are signals and noises, physicists try to identify signals by modeling them, whereas statisticians oppositely try to model noise to identify signals. In this study, we applied the statisticians' concept of signal detection of physics data with small-size samples and high dimensions without modeling the signals. Most of the data in nature, whether noises or signals, are assumed to be generated by dynamical systems; thus, there is essentially no distinction between these generating processes. We propose that the correlation length of a dynamical system and the number of samples are crucial for the practical definition of noise variables among the signal variables generated by such a system. Since variables with short-term correlations reach normal distributions faster as the number of samples decreases, they are regarded to be ``noise-like'' variables, whereas variables with opposite properties are ``signal-like'' variables. Normality tests are not effective for data of small-size samples with high dimensions. Therefore, we modeled noises on the basis of the property of a noise variable, that is, the uniformity of the histogram of the probability that a variable is a noise. We devised a method of detecting signal variables from the structural change of the histogram according to the decrease in the number of samples. We applied our method to the data generated by globally coupled map, which can produce time series data with different correlation lengths, and also applied to gene expression data, which are typical static data of small-size samples with high dimensions, and we successfully detected signal variables from them. Moreover, we verified the assumption that the gene expression data also potentially have a dynamical system as their generation model, and found that the assumption is compatible with the results of signal extraction.

Interpretable Conservation Law Estimation by Deriving the Symmetries of Dynamics from Trained Deep Neural Networks

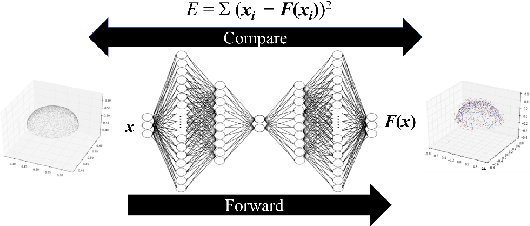
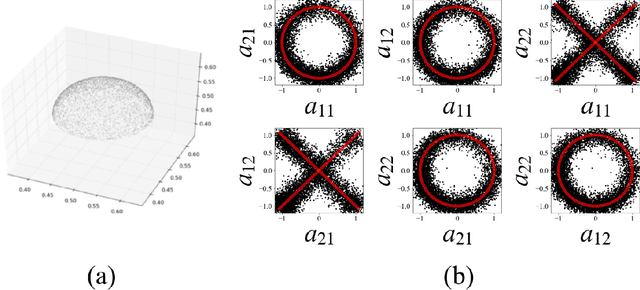
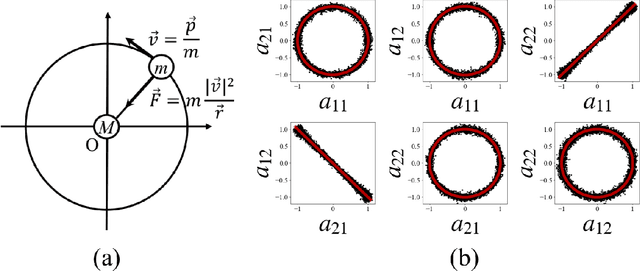
As deep neural networks (DNN) have the ability to model the distribution of datasets as a low-dimensional manifold, we propose a method to extract the coordinate transformation that makes a dataset distribution invariant by sampling DNNs using the replica exchange Monte-Carlo method. In addition, we derive the relation between the canonical transformation that makes the Hamiltonian invariant (a necessary condition for Noether's theorem) and the symmetry of the manifold structure of the time series data of the dynamical system. By integrating this knowledge with the method described above, we propose a method to estimate the interpretable conservation laws from the time-series data. Furthermore, we verified the efficiency of the proposed methods in primitive cases and large scale collective motion in metastable state.

Semi-flat minima and saddle points by embedding neural networks to overparameterization

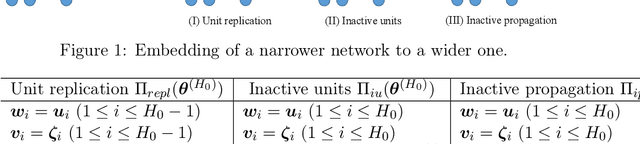
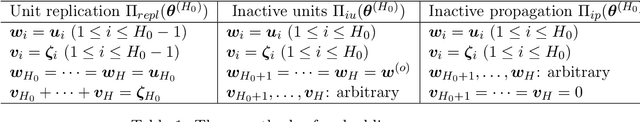
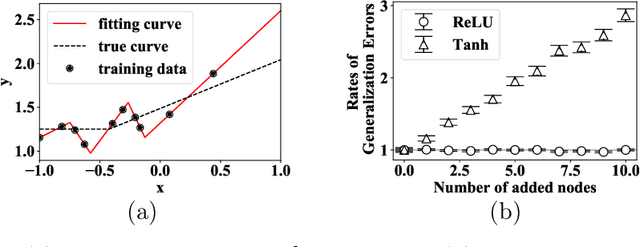
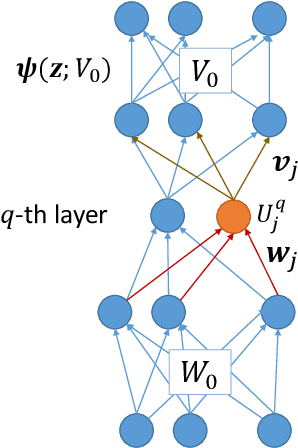
We theoretically study the landscape of the training error for neural networks in overparameterized cases. We consider three basic methods for embedding a network into a wider one with more hidden units, and discuss whether a minimum point of the narrower network gives a minimum or saddle point of the wider one. Our results show that the networks with smooth and ReLU activation have different partially flat landscapes around the embedded point. We also relate these results to a difference of their generalization abilities in overparameterized realization.

Bayesian Spectral Deconvolution Based on Poisson Distribution: Bayesian Measurement and Virtual Measurement Analytics (VMA)

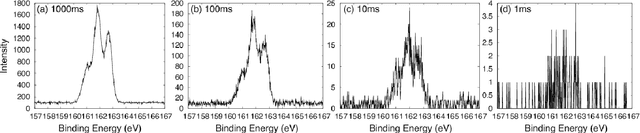
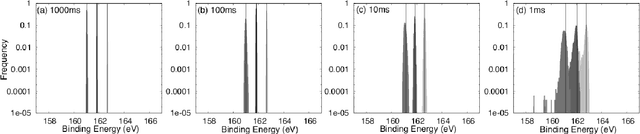
In this paper, we propose a new method of Bayesian measurement for spectral deconvolution, which regresses spectral data into the sum of unimodal basis function such as Gaussian or Lorentzian functions. Bayesian measurement is a framework for considering not only the target physical model but also the measurement model as a probabilistic model, and enables us to estimate the parameter of a physical model with its confidence interval through a Bayesian posterior distribution given a measurement data set. The measurement with Poisson noise is one of the most effective system to apply our proposed method. Since the measurement time is strongly related to the signal-to-noise ratio for the Poisson noise model, Bayesian measurement with Poisson noise model enables us to clarify the relationship between the measurement time and the limit of estimation. In this study, we establish the probabilistic model with Poisson noise for spectral deconvolution. Bayesian measurement enables us to perform virtual and computer simulation for a certain measurement through the established probabilistic model. This property is called "Virtual Measurement Analytics(VMA)" in this paper. We also show that the relationship between the measurement time and the limit of estimation can be extracted by using the proposed method in a simulation of synthetic data and real data for XPS measurement of MoS$_2$.