An integrated perspective of robustness in regression through the lens of the bias-variance trade-off

This paper presents an integrated perspective on robustness in regression. Specifically, we examine the relationship between traditional outlier-resistant robust estimation and robust optimization, which focuses on parameter estimation resistant to imaginary dataset-perturbations. While both are commonly regarded as robust methods, these concepts demonstrate a bias-variance trade-off, indicating that they follow roughly converse strategies.

A stochastic optimization approach to train non-linear neural networks with a higher-order variation regularization

While highly expressive parametric models including deep neural networks have an advantage to model complicated concepts, training such highly non-linear models is known to yield a high risk of notorious overfitting. To address this issue, this study considers a $(k,q)$th order variation regularization ($(k,q)$-VR), which is defined as the $q$th-powered integral of the absolute $k$th order derivative of the parametric models to be trained; penalizing the $(k,q)$-VR is expected to yield a smoother function, which is expected to avoid overfitting. Particularly, $(k,q)$-VR encompasses the conventional (general-order) total variation with $q=1$. While the $(k,q)$-VR terms applied to general parametric models are computationally intractable due to the integration, this study provides a stochastic optimization algorithm, that can efficiently train general models with the $(k,q)$-VR without conducting explicit numerical integration. The proposed approach can be applied to the training of even deep neural networks whose structure is arbitrary, as it can be implemented by only a simple stochastic gradient descent algorithm and automatic differentiation. Our numerical experiments demonstrate that the neural networks trained with the $(k,q)$-VR terms are more ``resilient'' than those with the conventional parameter regularization. The proposed algorithm also can be extended to the physics-informed training of neural networks (PINNs).

A stochastic optimization approach to minimize robust density power-based divergences for general parametric density models

Density power divergence (DPD) [Basu et al. (1998), Biometrika], which is designed to estimate the underlying distribution of the observations robustly against outliers, comprises an integral term of the power of the parametric density models to be estimated. While the explicit form of the integral term can be obtained for some specific densities (such as normal density and exponential density), its computational intractability has prohibited the application of DPD-based estimation to more general parametric densities, over a quarter of a century since the proposal of DPD. This study proposes a simple stochastic optimization approach to minimize DPD for general parametric density models and explains its adequacy by referring to conventional theories on stochastic optimization. The proposed approach also can be applied to the minimization of another density power-based $\gamma$-divergence with the aid of unnormalized models.

Forecasting of the development of a partially-observed dynamical time series with the aid of time-invariance and linearity

A dynamical system produces a dependent multivariate sequence called dynamical time series, developed with an evolution function. As variables in the dynamical time series at the current time-point usually depend on the whole variables in the previous time-point, existing studies forecast the variables at the future time-point by estimating the evolution function. However, some variables in the dynamical time-series are missing in some practical situations. In this study, we propose an autoregressive with slack time series (ARS) model. ARS model involves the simultaneous estimation of the evolution function and the underlying missing variables as a slack time series, with the aid of the time-invariance and linearity of the dynamical system. This study empirically demonstrates the effectiveness of the proposed ARS model.

An interpretable neural network-based non-proportional odds model for ordinal regression with continuous response

This paper proposes an interpretable neural network-based non-proportional odds model (N$^3$POM) for ordinal regression, where the response variable can take not only discrete but also continuous values, and the regression coefficients vary depending on the predicting ordinal response. In contrast to conventional approaches estimating the linear coefficients of regression directly from the discrete response, we train a non-linear neural network that outputs the linear coefficients by taking the response as its input. By virtue of the neural network, N$^3$POM may have flexibility while preserving the interpretability of the conventional ordinal regression. We show a sufficient condition so that the predicted conditional cumulative probability~(CCP) satisfies the monotonicity constraint locally over a user-specified region in the covariate space; we also provide a monotonicity-preserving stochastic (MPS) algorithm for training the neural network adequately.

A Greedy and Optimistic Approach to Clustering with a Specified Uncertainty of Covariates

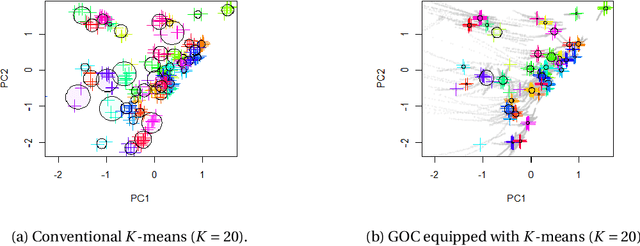
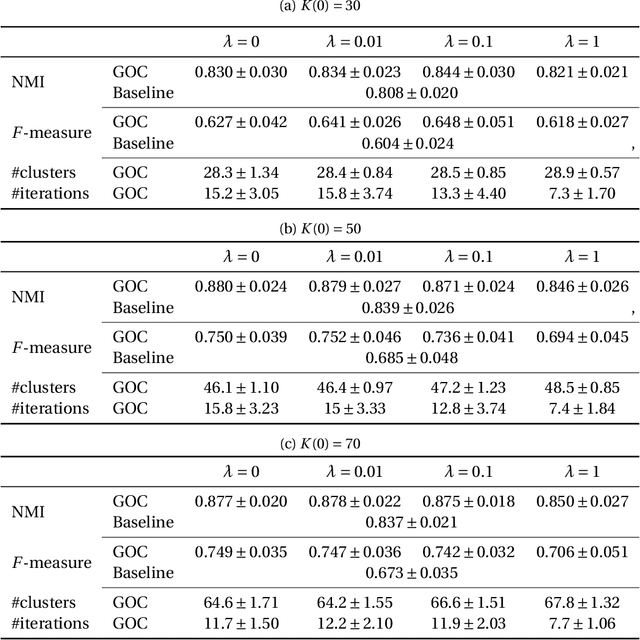
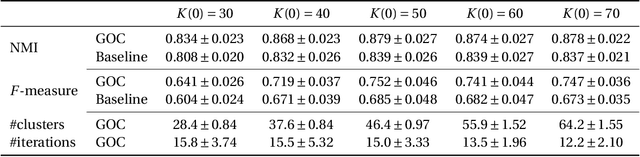
In this study, we examine a clustering problem in which the covariates of each individual element in a dataset are associated with an uncertainty specific to that element. More specifically, we consider a clustering approach in which a pre-processing applying a non-linear transformation to the covariates is used to capture the hidden data structure. To this end, we approximate the sets representing the propagated uncertainty for the pre-processed features empirically. To exploit the empirical uncertainty sets, we propose a greedy and optimistic clustering (GOC) algorithm that finds better feature candidates over such sets, yielding more condensed clusters. As an important application, we apply the GOC algorithm to synthetic datasets of the orbital properties of stars generated through our numerical simulation mimicking the formation process of the Milky Way. The GOC algorithm demonstrates an improved performance in finding sibling stars originating from the same dwarf galaxy. These realistic datasets have also been made publicly available.

Improving Nonparametric Classification via Local Radial Regression with an Application to Stock Prediction

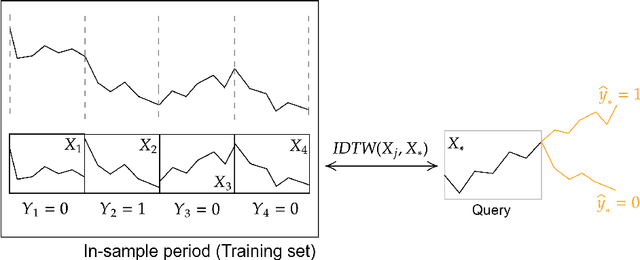
For supervised classification problems, this paper considers estimating the query's label probability through local regression using observed covariates. Well-known nonparametric kernel smoother and $k$-nearest neighbor ($k$-NN) estimator, which take label average over a ball around the query, are consistent but asymptotically biased particularly for a large radius of the ball. To eradicate such bias, local polynomial regression (LPoR) and multiscale $k$-NN (MS-$k$-NN) learn the bias term by local regression around the query and extrapolate it to the query itself. However, their theoretical optimality has been shown for the limit of the infinite number of training samples. For correcting the asymptotic bias with fewer observations, this paper proposes a local radial regression (LRR) and its logistic regression variant called local radial logistic regression (LRLR), by combining the advantages of LPoR and MS-$k$-NN. The idea is simple: we fit the local regression to observed labels by taking the radial distance as the explanatory variable and then extrapolate the estimated label probability to zero distance. Our numerical experiments, including real-world datasets of daily stock indices, demonstrate that LRLR outperforms LPoR and MS-$k$-NN.

A generalization gap estimation for overparameterized models via the Langevin functional variance

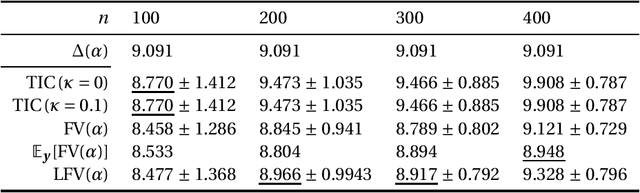
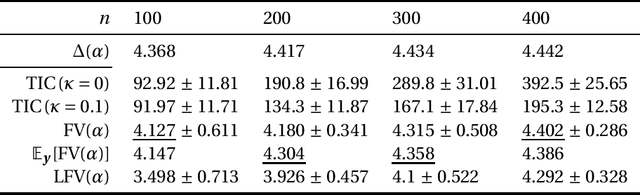
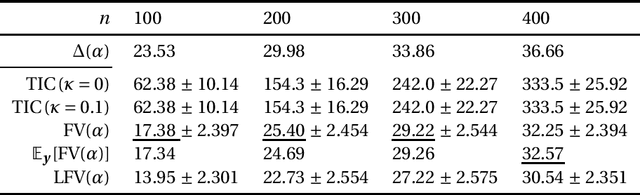
This paper discusses the estimation of the generalization gap, the difference between a generalization error and an empirical error, for overparameterized models (e.g., neural networks). We first show that a functional variance, a key concept in defining a widely-applicable information criterion, characterizes the generalization gap even in overparameterized settings where a conventional theory cannot be applied. We also propose a computationally efficient approximation of the function variance, the Langevin approximation of the functional variance (Langevin FV). This method leverages only the $1$st-order gradient of the squared loss function, without referencing the $2$nd-order gradient; this ensures that the computation is efficient and the implementation is consistent with gradient-based optimization algorithms. We demonstrate the Langevin FV numerically by estimating the generalization gaps of overparameterized linear regression and non-linear neural network models.

Minimax Analysis for Inverse Risk in Nonparametric Planer Invertible Regression

We study a minimax risk of estimating inverse functions on a plane, while keeping an estimator is also invertible. Learning invertibility from data and exploiting an invertible estimator are used in many domains, such as statistics, econometrics, and machine learning. Although the consistency and universality of invertible estimators have been well investigated, analysis on the efficiency of these methods is still under development. In this study, we study a minimax risk for estimating invertible bi-Lipschitz functions on a square in a $2$-dimensional plane. We first introduce an inverse $L^2$-risk to evaluate an estimator which preserves invertibility. Then, we derive lower and upper rates for a minimax inverse risk by exploiting a representation of invertible functions using level-sets. To obtain an upper bound, we develop an estimator asymptotically almost everywhere invertible, whose risk attains the derived minimax lower rate up to logarithmic factors. The derived minimax rate corresponds to that of the non-invertible bi-Lipschitz function, which rejects the expectation of whether invertibility improves the minimax rate, similar to other shape constraints.

Stochastic Neighbor Embedding of Multimodal Relational Data for Image-Text Simultaneous Visualization

Multimodal relational data analysis has become of increasing importance in recent years, for exploring across different domains of data, such as images and their text tags obtained from social networking services (e.g., Flickr). A variety of data analysis methods have been developed for visualization; to give an example, t-Stochastic Neighbor Embedding (t-SNE) computes low-dimensional feature vectors so that their similarities keep those of the observed data vectors. However, t-SNE is designed only for a single domain of data but not for multimodal data; this paper aims at visualizing multimodal relational data consisting of data vectors in multiple domains with relations across these vectors. By extending t-SNE, we herein propose Multimodal Relational Stochastic Neighbor Embedding (MR-SNE), that (1) first computes augmented relations, where we observe the relations across domains and compute those within each of domains via the observed data vectors, and (2) jointly embeds the augmented relations to a low-dimensional space. Through visualization of Flickr and Animal with Attributes 2 datasets, proposed MR-SNE is compared with other graph embedding-based approaches; MR-SNE demonstrates the promising performance.