Dual Riemannian Newton Method on Statistical Manifolds

In probabilistic modeling, parameter estimation is commonly formulated as a minimization problem on a parameter manifold. Optimization in such spaces requires geometry-aware methods that respect the underlying information structure. While the natural gradient leverages the Fisher information metric as a form of Riemannian gradient descent, it remains a first-order method and often exhibits slow convergence near optimal solutions. Existing second-order manifold algorithms typically rely on the Levi-Civita connection, thus overlooking the dual-connection structure that is central to information geometry. We propose the dual Riemannian Newton method, a Newton-type optimization algorithm on manifolds endowed with a metric and a pair of dual affine connections. The dual Riemannian Newton method explicates how duality shapes second-order updates: when the retraction (a local surrogate of the exponential map) is defined by one connection, the associated Newton equation is posed with its dual. We establish local quadratic convergence and validate the theory with experiments on representative statistical models. Thus, the dual Riemannian Newton method thus delivers second-order efficiency while remaining compatible with the dual structures that underlie modern information-geometric learning and inference.

Duality induced by an embedding structure of determinantal point process

This paper investigates the information geometrical structure of a determinantal point process (DPP). It demonstrates that a DPP is embedded in the exponential family of log-linear models. The extent of deviation from an exponential family is analyzed using the $\mathrm{e}$-embedding curvature tensor, which identifies partially flat parameters of a DPP. On the basis of this embedding structure, the duality related to a marginal kernel and an $L$-ensemble kernel is discovered.

A generalization gap estimation for overparameterized models via the Langevin functional variance

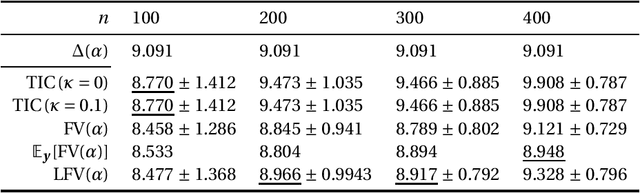
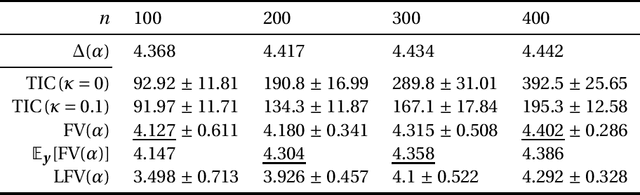
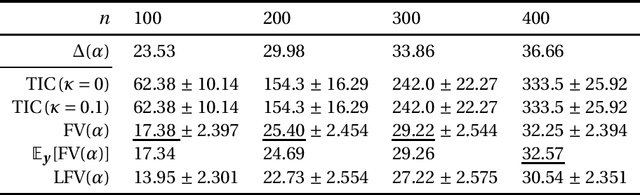
This paper discusses the estimation of the generalization gap, the difference between a generalization error and an empirical error, for overparameterized models (e.g., neural networks). We first show that a functional variance, a key concept in defining a widely-applicable information criterion, characterizes the generalization gap even in overparameterized settings where a conventional theory cannot be applied. We also propose a computationally efficient approximation of the function variance, the Langevin approximation of the functional variance (Langevin FV). This method leverages only the $1$st-order gradient of the squared loss function, without referencing the $2$nd-order gradient; this ensures that the computation is efficient and the implementation is consistent with gradient-based optimization algorithms. We demonstrate the Langevin FV numerically by estimating the generalization gaps of overparameterized linear regression and non-linear neural network models.

Posterior Covariance Information Criterion

We introduce an information criterion, PCIC, for predictive evaluation based on quasi-posterior distributions. It is regarded as a natural generalisation of the widely applicable information criterion (WAIC) and can be computed via a single Markov chain Monte Carlo run. PCIC is useful in a variety of predictive settings that are not well dealt with in WAIC, including weighted likelihood inference and quasi-Bayesian prediction

Learning partially ranked data based on graph regularization

Ranked data appear in many different applications, including voting and consumer surveys. There often exhibits a situation in which data are partially ranked. Partially ranked data is thought of as missing data. This paper addresses parameter estimation for partially ranked data under a (possibly) non-ignorable missing mechanism. We propose estimators for both complete rankings and missing mechanisms together with a simple estimation procedure. Our estimation procedure leverages a graph regularization in conjunction with the Expectation-Maximization algorithm. Our estimation procedure is theoretically guaranteed to have the convergence properties. We reduce a modeling bias by allowing a non-ignorable missing mechanism. In addition, we avoid the inherent complexity within a non-ignorable missing mechanism by introducing a graph regularization. The experimental results demonstrate that the proposed estimators work well under non-ignorable missing mechanisms.