LIG: Layer-wise Integrated Gradients for Within-Layer Flow Analysis in Transformers

Transformers achieve strong performance, but their internal computations remain opaque. We view each Transformer layer as a dynamic graph whose nodes are token representations and per-head attention outputs, with Multi-Head Attention (ATT) and MLP as module boundaries. On this graph we use LIG (Layer-wise Integrated Gradients), which applies set-to-set Integrated Gradients (IG) at nonlinear module boundaries. Set-to-set IG applies IG to a map from a set of input token representations to a set of output representations, evaluating token-to-token contributions, which is not standard in prior IG applications. This extends IG from the usual scalar-objective setting to set-to-set maps via an L2 scalarization, and composes within-layer contributions in the spirit of Layer-wise Relevance Propagation (LRP), with IG completeness playing the role of LRP-style conservation at each boundary. We use LIG to analyze (i) the agreement between module-wise composition and layer-whole attribution under an L2 criterion, and (ii) within-layer information flow by tracing separated ATT and MLP contributions. On BERT-base and PTB, configurations that best preserved within-layer consistency used the target token's embedding as the ATT baseline and either the ATT output at a=0 or Zero as the MLP baseline. We therefore present LIG as a diagnostic XAI tool at module-boundary granularity, without model-specific retraining or per-operation interpreter design. Code is available at https://github.com/eightsuzuki/layer-wise-integrated-gradients.

From DPPs to $k$-DPPs: identifiability analysis via spectral decomposition

We study the geometry of determinantal point processes (DPPs) through the spectral decomposition $L=UΛU^{\top}$. The spectrum $Λ$ governs the cardinality distribution via elementary symmetric polynomials, while the eigenspace orientation $U$ governs the conditional law within each fixed-cardinality stratum. Conditioning on cardinality $k$ yields the $k$-DPP, for which the identifiability structure changes fundamentally: the spectral parameter becomes identifiable only up to a common scale, and the eigenspace rotation parameter is identifiable only through squared minors of the eigenvector matrix. We characterize the identifiability gap precisely, via three explicit invariances (scale, sign similarity, and eigenspace rotation) and a dimension-counting theorem showing the existence of additional continuous non-identifiability whenever $\binom{N}{k}<N(N+1)/2$. In contrast, for the full DPP the non-identifiability comes only from the discrete sign similarity.

Sobolev--Ricci Curvature

Ricci curvature is a fundamental concept in differential geometry for encoding local geometric structure, and its graph-based analogues have recently gained prominence as practical tools for reweighting, pruning, and reshaping network geometry. We propose Sobolev-Ricci Curvature (SRC), a graph Ricci curvature canonically induced by Sobolev transport geometry, which admits efficient evaluation via a tree-metric Sobolev structure on neighborhood measures. We establish two consistency behaviors that anchor SRC to classical transport curvature: (i) on trees endowed with the length measure, SRC recovers Ollivier-Ricci curvature (ORC) in the canonical W1 setting, and (ii) SRC vanishes in the Dirac limit, matching the flat case of measure-theoretic Ricci curvature. We demonstrate SRC as a reusable curvature primitive in two representative pipelines. We define Sobolev-Ricci Flow by replacing ORC with SRC in a Ricci-flow-style reweighting rule, and we use SRC for curvature-guided edge pruning aimed at preserving manifold structure. Overall, SRC provides a transport-based foundation for scalable curvature-driven graph transformation and manifold-oriented pruning.

An $(ε,δ)$-accurate level set estimation with a stopping criterion

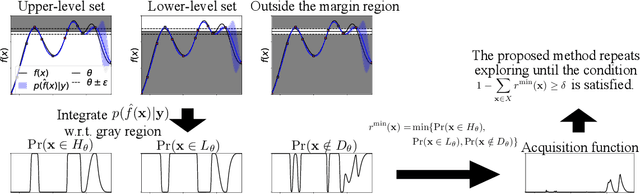
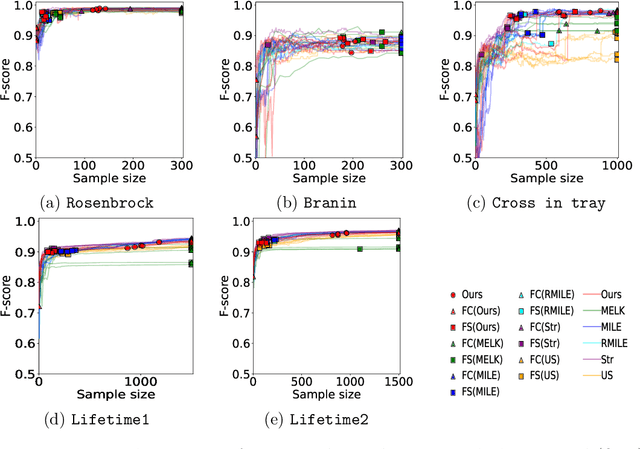
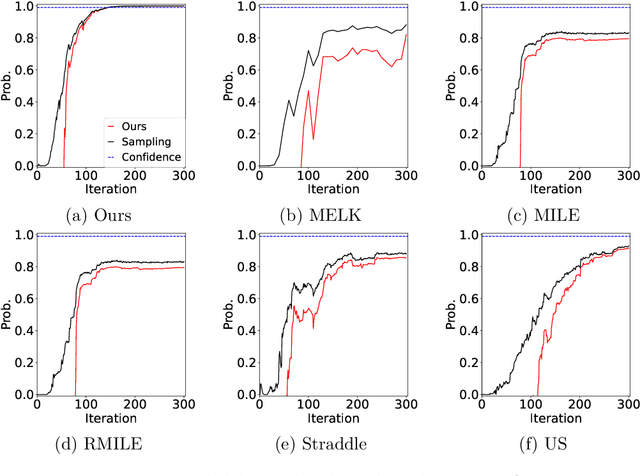
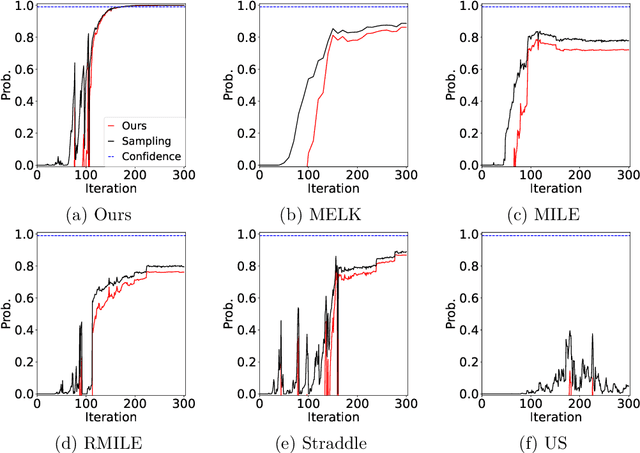
The level set estimation problem seeks to identify regions within a set of candidate points where an unknown and costly to evaluate function's value exceeds a specified threshold, providing an efficient alternative to exhaustive evaluations of function values. Traditional methods often use sequential optimization strategies to find $\epsilon$-accurate solutions, which permit a margin around the threshold contour but frequently lack effective stopping criteria, leading to excessive exploration and inefficiencies. This paper introduces an acquisition strategy for level set estimation that incorporates a stopping criterion, ensuring the algorithm halts when further exploration is unlikely to yield improvements, thereby reducing unnecessary function evaluations. We theoretically prove that our method satisfies $\epsilon$-accuracy with a confidence level of $1 - \delta$, addressing a key gap in existing approaches. Furthermore, we show that this also leads to guarantees on the lower bounds of performance metrics such as F-score. Numerical experiments demonstrate that the proposed acquisition function achieves comparable precision to existing methods while confirming that the stopping criterion effectively terminates the algorithm once adequate exploration is completed.

Scalable Sobolev IPM for Probability Measures on a Graph

We investigate the Sobolev IPM problem for probability measures supported on a graph metric space. Sobolev IPM is an important instance of integral probability metrics (IPM), and is obtained by constraining a critic function within a unit ball defined by the Sobolev norm. In particular, it has been used to compare probability measures and is crucial for several theoretical works in machine learning. However, to our knowledge, there are no efficient algorithmic approaches to compute Sobolev IPM effectively, which hinders its practical applications. In this work, we establish a relation between Sobolev norm and weighted $L^p$-norm, and leverage it to propose a \emph{novel regularization} for Sobolev IPM. By exploiting the graph structure, we demonstrate that the regularized Sobolev IPM provides a \emph{closed-form} expression for fast computation. This advancement addresses long-standing computational challenges, and paves the way to apply Sobolev IPM for practical applications, even in large-scale settings. Additionally, the regularized Sobolev IPM is negative definite. Utilizing this property, we design positive-definite kernels upon the regularized Sobolev IPM, and provide preliminary evidences of their advantages on document classification and topological data analysis for measures on a graph.

Orlicz-Sobolev Transport for Unbalanced Measures on a Graph

Moving beyond $L^p$ geometric structure, Orlicz-Wasserstein (OW) leverages a specific class of convex functions for Orlicz geometric structure. While OW remarkably helps to advance certain machine learning approaches, it has a high computational complexity due to its two-level optimization formula. Recently, Le et al. (2024) exploits graph structure to propose generalized Sobolev transport (GST), i.e., a scalable variant for OW. However, GST assumes that input measures have the same mass. Unlike optimal transport (OT), it is nontrivial to incorporate a mass constraint to extend GST for measures on a graph, possibly having different total mass. In this work, we propose to take a step back by considering the entropy partial transport (EPT) for nonnegative measures on a graph. By leveraging Caffarelli & McCann (2010)'s observations, EPT can be reformulated as a standard complete OT between two corresponding balanced measures. Consequently, we develop a novel EPT with Orlicz geometric structure, namely Orlicz-EPT, for unbalanced measures on a graph. Especially, by exploiting the dual EPT formulation and geometric structures of the graph-based Orlicz-Sobolev space, we derive a novel regularization to propose Orlicz-Sobolev transport (OST). The resulting distance can be efficiently computed by simply solving a univariate optimization problem, unlike the high-computational two-level optimization problem for Orlicz-EPT. Additionally, we derive geometric structures for the OST and draw its relations to other transport distances. We empirically show that OST is several-order faster than Orlicz-EPT. We further illustrate preliminary evidences on the advantages of OST for document classification, and several tasks in topological data analysis.

A Family of Distributions of Random Subsets for Controlling Positive and Negative Dependence

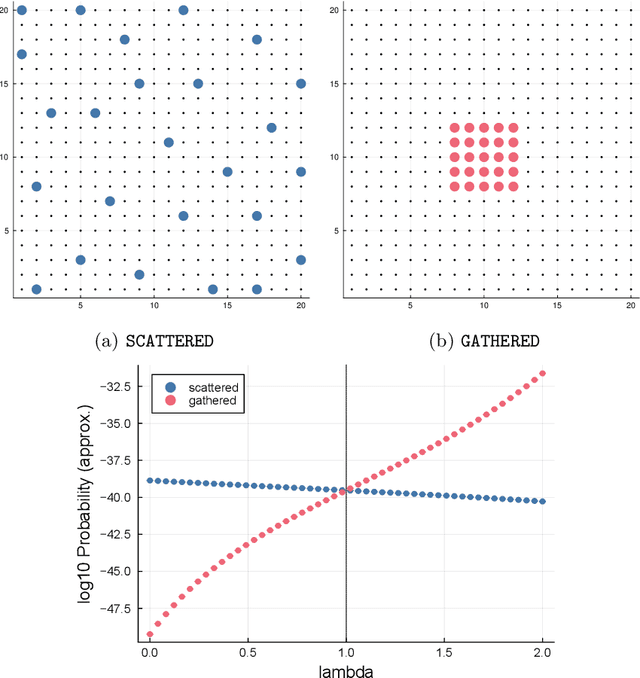
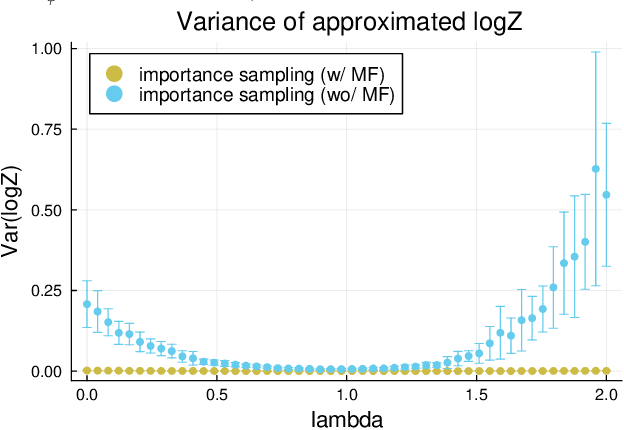
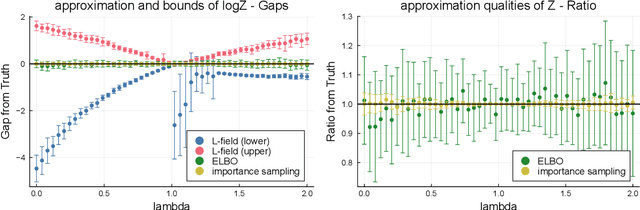
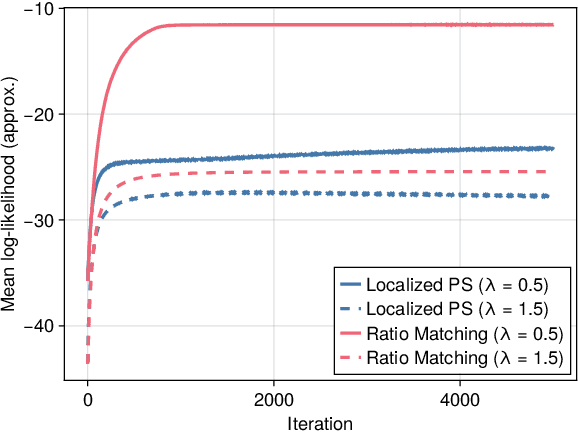
Positive and negative dependence are fundamental concepts that characterize the attractive and repulsive behavior of random subsets. Although some probabilistic models are known to exhibit positive or negative dependence, it is challenging to seamlessly bridge them with a practicable probabilistic model. In this study, we introduce a new family of distributions, named the discrete kernel point process (DKPP), which includes determinantal point processes and parts of Boltzmann machines. We also develop some computational methods for probabilistic operations and inference with DKPPs, such as calculating marginal and conditional probabilities and learning the parameters. Our numerical experiments demonstrate the controllability of positive and negative dependence and the effectiveness of the computational methods for DKPPs.

Duality induced by an embedding structure of determinantal point process

This paper investigates the information geometrical structure of a determinantal point process (DPP). It demonstrates that a DPP is embedded in the exponential family of log-linear models. The extent of deviation from an exponential family is analyzed using the $\mathrm{e}$-embedding curvature tensor, which identifies partially flat parameters of a DPP. On the basis of this embedding structure, the duality related to a marginal kernel and an $L$-ensemble kernel is discovered.

A Short Survey on Importance Weighting for Machine Learning

Importance weighting is a fundamental procedure in statistics and machine learning that weights the objective function or probability distribution based on the importance of the instance in some sense. The simplicity and usefulness of the idea has led to many applications of importance weighting. For example, it is known that supervised learning under an assumption about the difference between the training and test distributions, called distribution shift, can guarantee statistically desirable properties through importance weighting by their density ratio. This survey summarizes the broad applications of importance weighting in machine learning and related research.

Scalable Counterfactual Distribution Estimation in Multivariate Causal Models

We consider the problem of estimating the counterfactual joint distribution of multiple quantities of interests (e.g., outcomes) in a multivariate causal model extended from the classical difference-in-difference design. Existing methods for this task either ignore the correlation structures among dimensions of the multivariate outcome by considering univariate causal models on each dimension separately and hence produce incorrect counterfactual distributions, or poorly scale even for moderate-size datasets when directly dealing with such multivariate causal model. We propose a method that alleviates both issues simultaneously by leveraging a robust latent one-dimensional subspace of the original high-dimension space and exploiting the efficient estimation from the univariate causal model on such space. Since the construction of the one-dimensional subspace uses information from all the dimensions, our method can capture the correlation structures and produce good estimates of the counterfactual distribution. We demonstrate the advantages of our approach over existing methods on both synthetic and real-world data.