Density Ratio-based Causal Discovery from Bivariate Continuous-Discrete Data

This paper proposes a causal discovery method for mixed bivariate data consisting of one continuous and one discrete variable. Existing constraint-based approaches are ineffective in the bivariate setting, as they rely on conditional independence tests that are not suited to bivariate data. Score-based methods either impose strong distributional assumptions or face challenges in fairly comparing causal directions between variables of different types, due to differences in their information content. We introduce a novel approach that determines causal direction by analyzing the monotonicity of the conditional density ratio of the continuous variable, conditioned on different values of the discrete variable. Our theoretical analysis shows that the conditional density ratio exhibits monotonicity when the continuous variable causes the discrete variable, but not in the reverse direction. This property provides a principled basis for comparing causal directions between variables of different types, free from strong distributional assumptions and bias arising from differences in their information content. We demonstrate its effectiveness through experiments on both synthetic and real-world datasets, showing superior accuracy compared to existing methods.

Causal Additive Models with Unobserved Causal Paths and Backdoor Paths

Causal additive models have been employed as tractable yet expressive frameworks for causal discovery involving hidden variables. State-of-the-art methodologies suggest that determining the causal relationship between a pair of variables is infeasible in the presence of an unobserved backdoor or an unobserved causal path. Contrary to this assumption, we theoretically show that resolving the causal direction is feasible in certain scenarios by incorporating two novel components into the theory. The first component introduces a novel characterization of regression sets within independence between regression residuals. The second component leverages conditional independence among the observed variables. We also provide a search algorithm that integrates these innovations and demonstrate its competitive performance against existing methods.

Causal-discovery-based root-cause analysis and its application in time-series prediction error diagnosis

Recent rapid advancements of machine learning have greatly enhanced the accuracy of prediction models, but most models remain "black boxes", making prediction error diagnosis challenging, especially with outliers. This lack of transparency hinders trust and reliability in industrial applications. Heuristic attribution methods, while helpful, often fail to capture true causal relationships, leading to inaccurate error attributions. Various root-cause analysis methods have been developed using Shapley values, yet they typically require predefined causal graphs, limiting their applicability for prediction errors in machine learning models. To address these limitations, we introduce the Causal-Discovery-based Root-Cause Analysis (CD-RCA) method that estimates causal relationships between the prediction error and the explanatory variables, without needing a pre-defined causal graph. By simulating synthetic error data, CD-RCA can identify variable contributions to outliers in prediction errors by Shapley values. Extensive simulations show CD-RCA outperforms current heuristic attribution methods, and a sensitivity analysis reveals new patterns where Shapley values may misattribute errors, paving the way for more accurate error attribution methods.

Counterfactual Explanations of Black-box Machine Learning Models using Causal Discovery with Applications to Credit Rating

Explainable artificial intelligence (XAI) has helped elucidate the internal mechanisms of machine learning algorithms, bolstering their reliability by demonstrating the basis of their predictions. Several XAI models consider causal relationships to explain models by examining the input-output relationships of prediction models and the dependencies between features. The majority of these models have been based their explanations on counterfactual probabilities, assuming that the causal graph is known. However, this assumption complicates the application of such models to real data, given that the causal relationships between features are unknown in most cases. Thus, this study proposed a novel XAI framework that relaxed the constraint that the causal graph is known. This framework leveraged counterfactual probabilities and additional prior information on causal structure, facilitating the integration of a causal graph estimated through causal discovery methods and a black-box classification model. Furthermore, explanatory scores were estimated based on counterfactual probabilities. Numerical experiments conducted employing artificial data confirmed the possibility of estimating the explanatory score more accurately than in the absence of a causal graph. Finally, as an application to real data, we constructed a classification model of credit ratings assigned by Shiga Bank, Shiga prefecture, Japan. We demonstrated the effectiveness of the proposed method in cases where the causal graph is unknown.

Integrating Large Language Models in Causal Discovery: A Statistical Causal Approach

In practical statistical causal discovery (SCD), embedding domain expert knowledge as constraints into the algorithm is widely accepted as significant for creating consistent meaningful causal models, despite the recognized challenges in systematic acquisition of the background knowledge. To overcome these challenges, this paper proposes a novel methodology for causal inference, in which SCD methods and knowledge based causal inference (KBCI) with a large language model (LLM) are synthesized through "statistical causal prompting (SCP)" for LLMs and prior knowledge augmentation for SCD. Experiments have revealed that GPT-4 can cause the output of the LLM-KBCI and the SCD result with prior knowledge from LLM-KBCI to approach the ground truth, and that the SCD result can be further improved, if GPT-4 undergoes SCP. Furthermore, it has been clarified that an LLM can improve SCD with its background knowledge, even if the LLM does not contain information on the dataset. The proposed approach can thus address challenges such as dataset biases and limitations, illustrating the potential of LLMs to improve data-driven causal inference across diverse scientific domains.

Use of Prior Knowledge to Discover Causal Additive Models with Unobserved Variables and its Application to Time Series Data

This paper proposes two methods for causal additive models with unobserved variables (CAM-UV). CAM-UV assumes that the causal functions take the form of generalized additive models and that latent confounders are present. First, we propose a method that leverages prior knowledge for efficient causal discovery. Then, we propose an extension of this method for inferring causality in time series data. The original CAM-UV algorithm differs from other existing causal function models in that it does not seek the causal order between observed variables, but rather aims to identify the causes for each observed variable. Therefore, the first proposed method in this paper utilizes prior knowledge, such as understanding that certain variables cannot be causes of specific others. Moreover, by incorporating the prior knowledge that causes precedes their effects in time, we extend the first algorithm to the second method for causal discovery in time series data. We validate the first proposed method by using simulated data to demonstrate that the accuracy of causal discovery increases as more prior knowledge is accumulated. Additionally, we test the second proposed method by comparing it with existing time series causal discovery methods, using both simulated data and real-world data.

Scalable Counterfactual Distribution Estimation in Multivariate Causal Models

We consider the problem of estimating the counterfactual joint distribution of multiple quantities of interests (e.g., outcomes) in a multivariate causal model extended from the classical difference-in-difference design. Existing methods for this task either ignore the correlation structures among dimensions of the multivariate outcome by considering univariate causal models on each dimension separately and hence produce incorrect counterfactual distributions, or poorly scale even for moderate-size datasets when directly dealing with such multivariate causal model. We propose a method that alleviates both issues simultaneously by leveraging a robust latent one-dimensional subspace of the original high-dimension space and exploiting the efficient estimation from the univariate causal model on such space. Since the construction of the one-dimensional subspace uses information from all the dimensions, our method can capture the correlation structures and produce good estimates of the counterfactual distribution. We demonstrate the advantages of our approach over existing methods on both synthetic and real-world data.

Causal-learn: Causal Discovery in Python

Causal discovery aims at revealing causal relations from observational data, which is a fundamental task in science and engineering. We describe $\textit{causal-learn}$, an open-source Python library for causal discovery. This library focuses on bringing a comprehensive collection of causal discovery methods to both practitioners and researchers. It provides easy-to-use APIs for non-specialists, modular building blocks for developers, detailed documentation for learners, and comprehensive methods for all. Different from previous packages in R or Java, $\textit{causal-learn}$ is fully developed in Python, which could be more in tune with the recent preference shift in programming languages within related communities. The library is available at https://github.com/py-why/causal-learn.

Discovery of Causal Additive Models in the Presence of Unobserved Variables

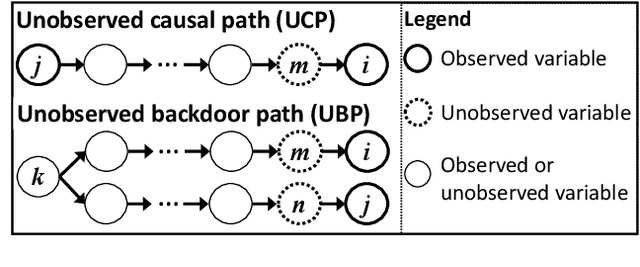
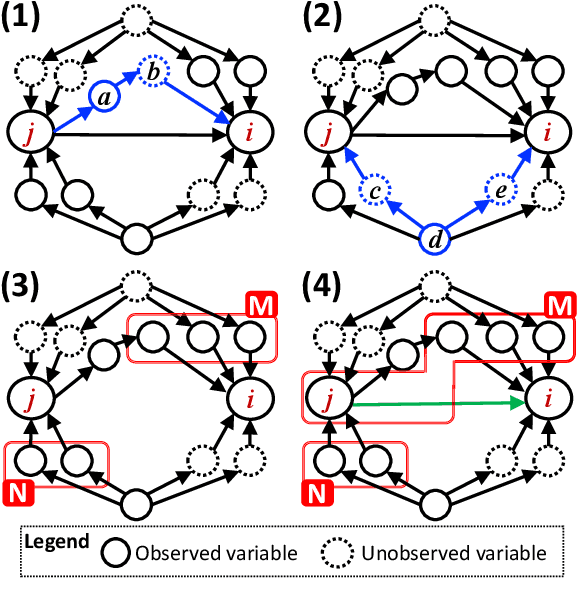
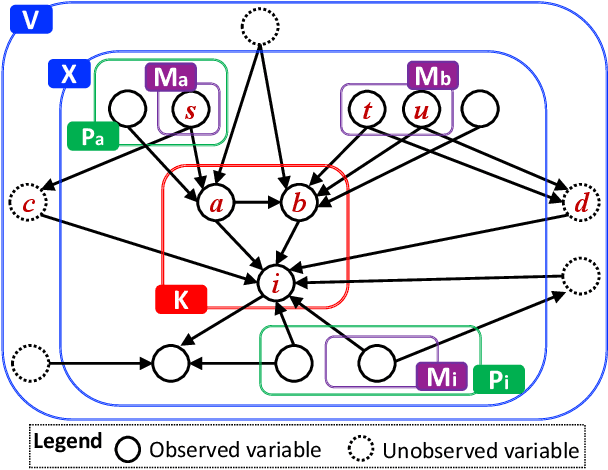
Causal discovery from data affected by unobserved variables is an important but difficult problem to solve. The effects that unobserved variables have on the relationships between observed variables are more complex in nonlinear cases than in linear cases. In this study, we focus on causal additive models in the presence of unobserved variables. Causal additive models exhibit structural equations that are additive in the variables and error terms. We take into account the presence of not only unobserved common causes but also unobserved intermediate variables. Our theoretical results show that, when the causal relationships are nonlinear and there are unobserved variables, it is not possible to identify all the causal relationships between observed variables through regression and independence tests. However, our theoretical results also show that it is possible to avoid incorrect inferences. We propose a method to identify all the causal relationships that are theoretically possible to identify without being biased by unobserved variables. The empirical results using artificial data and simulated functional magnetic resonance imaging (fMRI) data show that our method effectively infers causal structures in the presence of unobserved variables.

Causal Discovery with Multi-Domain LiNGAM for Latent Factors

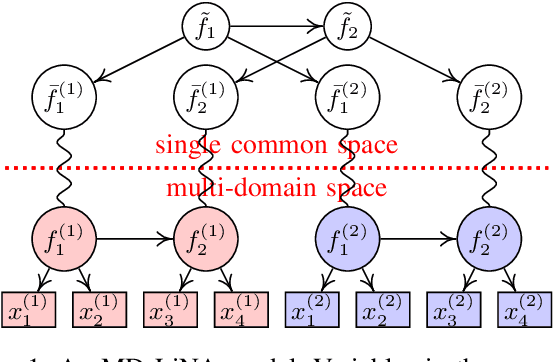
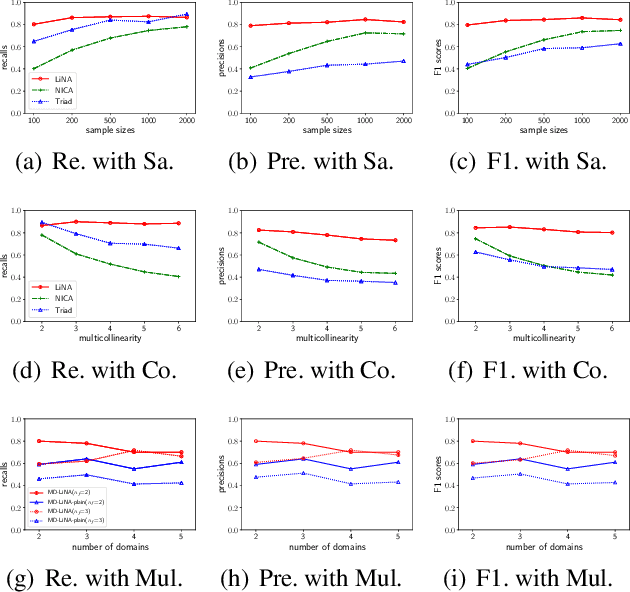
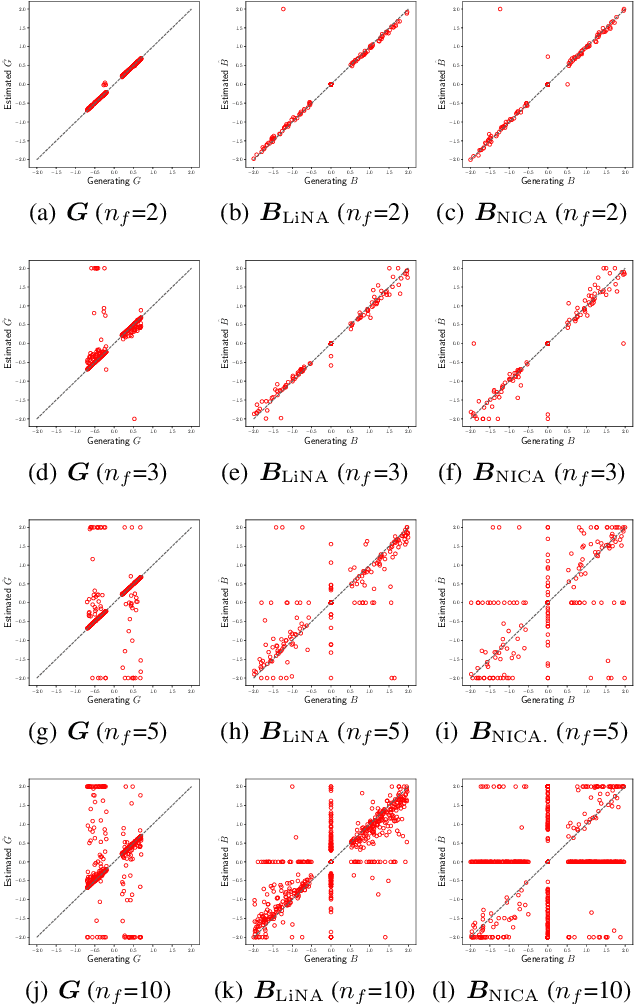
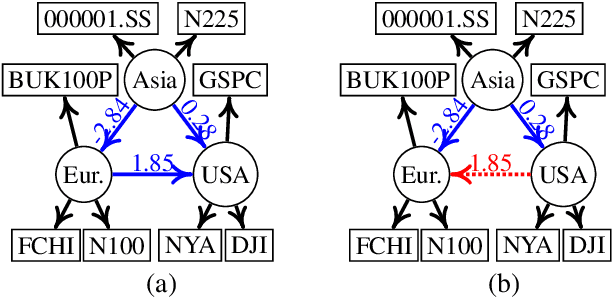
Discovering causal structures among latent factors from observed data is a particularly challenging problem, in which many empirical researchers are interested. Despite its success in certain degrees, existing methods focus on the single-domain observed data only, while in many scenarios data may be originated from distinct domains, e.g. in neuroinformatics. In this paper, we propose Multi-Domain Linear Non-Gaussian Acyclic Models for LAtent Factors (abbreviated as MD-LiNA model) to identify the underlying causal structure between latent factors (of interest), tackling not only single-domain observed data but multiple-domain ones, and provide its identification results. In particular, we first locate the latent factors and estimate the factor loadings matrix for each domain separately. Then to estimate the structure among latent factors (of interest), we derive a score function based on the characterization of independence relations between external influences and the dependence relations between multiple-domain latent factors and latent factors of interest, enforcing acyclicity, sparsity, and elastic net constraints. The resulting optimization thus produces asymptotically correct results. It also exhibits satisfactory capability in regimes of small sample sizes or highly-correlated variables and simultaneously estimates the causal directions and effects between latent factors. Experimental results on both synthetic and real-world data demonstrate the efficacy of our approach.