Scalable Causal Discovery from Recursive Nonlinear Data via Truncated Basis Function Scores and Tests

Learning graphical conditional independence structures from nonlinear, continuous or mixed data is a central challenge in machine learning and the sciences, and many existing methods struggle to scale to thousands of samples or hundreds of variables. We introduce two basis-expansion tools for scalable causal discovery. First, the Basis Function BIC (BF-BIC) score uses truncated additive expansions to approximate nonlinear dependencies. BF-BIC is theoretically consistent under additive models and extends to post-nonlinear (PNL) models via an invertible reparameterization. It remains robust under moderate interactions and supports mixed data through a degenerate-Gaussian embedding for discrete variables. In simulations with fully nonlinear neural causal models (NCMs), BF-BIC outperforms kernel- and constraint-based methods (e.g., KCI, RFCI) in both accuracy and runtime. Second, the Basis Function Likelihood Ratio Test (BF-LRT) provides an approximate conditional independence test that is substantially faster than kernel tests while retaining competitive accuracy. Extensive simulations and a real-data application to Canadian wildfire risk show that, when integrated into hybrid searches, BF-based methods enable interpretable and scalable causal discovery. Implementations are available in Python, R, and Java.

Efficient Latent Variable Causal Discovery: Combining Score Search and Targeted Testing

Learning causal structure from observational data is especially challenging when latent variables or selection bias are present. The Fast Causal Inference (FCI) algorithm addresses this setting but often performs exhaustive conditional independence tests across many subsets, leading to spurious independence claims, extra or missing edges, and unreliable orientations. We present a family of score-guided mixed-strategy causal search algorithms that build on this tradition. First, we introduce BOSS-FCI and GRaSP-FCI, straightforward variants of GFCI that substitute BOSS or GRaSP for FGES, thereby retaining correctness while incurring different scalability tradeoffs. Second, we develop FCI Targeted-testing (FCIT), a novel mixed-strategy method that improves upon these variants by replacing exhaustive all-subsets testing with targeted tests guided by BOSS, yielding well-formed PAGs with higher precision and efficiency. Finally, we propose a simple heuristic, LV-Dumb (also known as BOSS-POD), which bypasses latent-variable-specific reasoning and directly returns the PAG of the BOSS DAG. Although not strictly correct in the FCI sense, it scales better and often achieves superior accuracy in practice. Simulations and real-data analyses demonstrate that BOSS-FCI and GRaSP-FCI provide sound baselines, FCIT improves both efficiency and reliability, and LV-Dumb offers a practical heuristic with strong empirical performance. Together, these method highlight the value of score-guided and targeted strategies for scalable latent-variable causal discovery.

Fast Scalable and Accurate Discovery of DAGs Using the Best Order Score Search and Grow-Shrink Trees

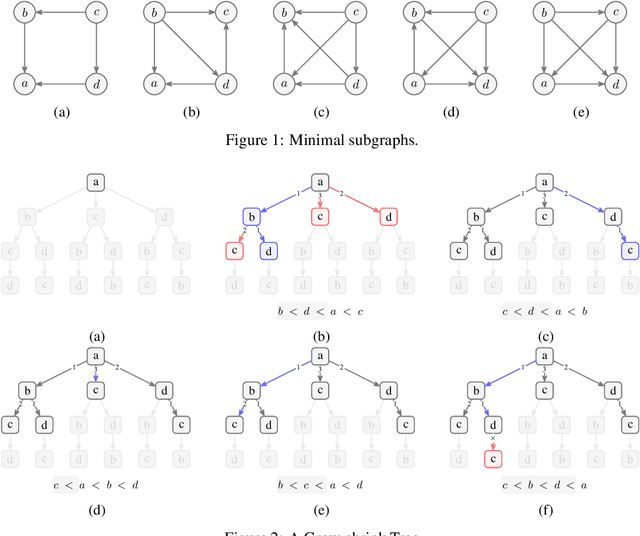
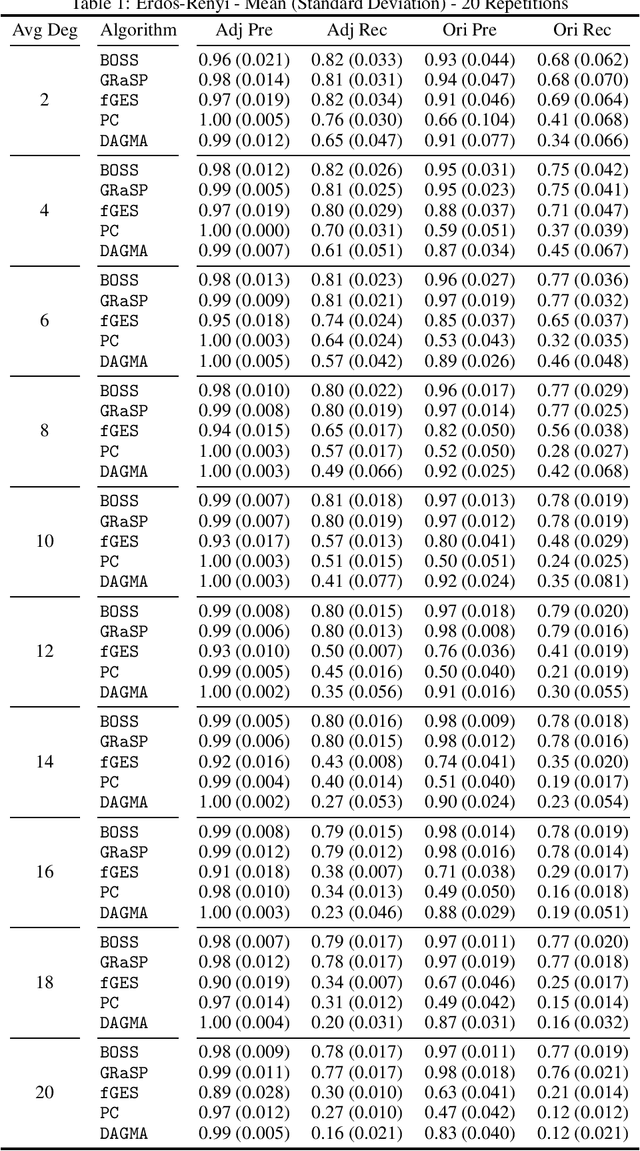
Learning graphical conditional independence structures is an important machine learning problem and a cornerstone of causal discovery. However, the accuracy and execution time of learning algorithms generally struggle to scale to problems with hundreds of highly connected variables -- for instance, recovering brain networks from fMRI data. We introduce the best order score search (BOSS) and grow-shrink trees (GSTs) for learning directed acyclic graphs (DAGs) in this paradigm. BOSS greedily searches over permutations of variables, using GSTs to construct and score DAGs from permutations. GSTs efficiently cache scores to eliminate redundant calculations. BOSS achieves state-of-the-art performance in accuracy and execution time, comparing favorably to a variety of combinatorial and gradient-based learning algorithms under a broad range of conditions. To demonstrate its practicality, we apply BOSS to two sets of resting-state fMRI data: simulated data with pseudo-empirical noise distributions derived from randomized empirical fMRI cortical signals and clinical data from 3T fMRI scans processed into cortical parcels. BOSS is available for use within the TETRAD project which includes Python and R wrappers.

Causal-learn: Causal Discovery in Python

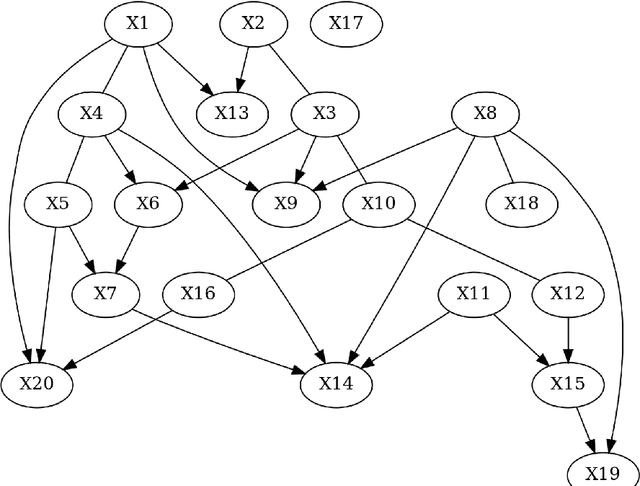
Causal discovery aims at revealing causal relations from observational data, which is a fundamental task in science and engineering. We describe $\textit{causal-learn}$, an open-source Python library for causal discovery. This library focuses on bringing a comprehensive collection of causal discovery methods to both practitioners and researchers. It provides easy-to-use APIs for non-specialists, modular building blocks for developers, detailed documentation for learners, and comprehensive methods for all. Different from previous packages in R or Java, $\textit{causal-learn}$ is fully developed in Python, which could be more in tune with the recent preference shift in programming languages within related communities. The library is available at https://github.com/py-why/causal-learn.

Greedy Relaxations of the Sparsest Permutation Algorithm

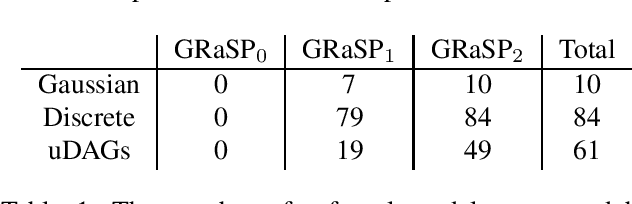
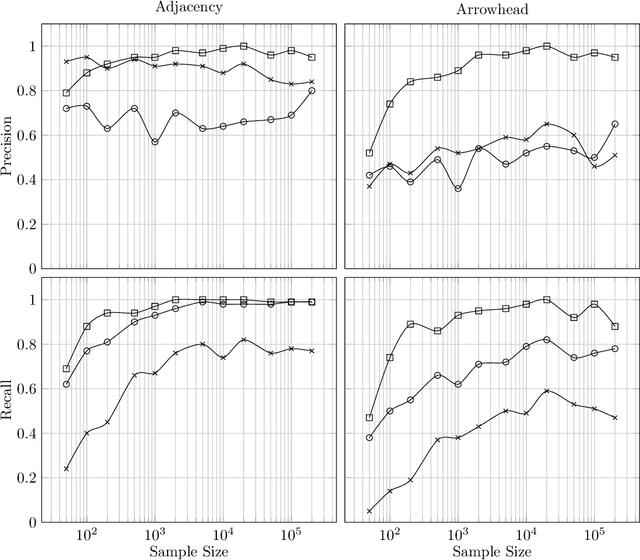
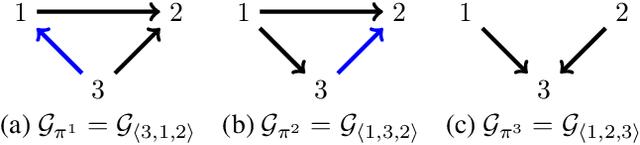
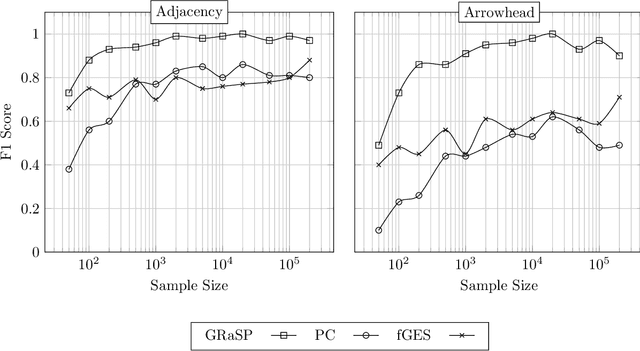
There has been an increasing interest in methods that exploit permutation reasoning to search for directed acyclic causal models, including the "Ordering Search" of Teyssier and Kohler and GSP of Solus, Wang and Uhler. We extend the methods of the latter by a permutation-based operation, tuck, and develop a class of algorithms, namely GRaSP, that are efficient and pointwise consistent under increasingly weaker assumptions than faithfulness. The most relaxed form of GRaSP outperforms many state-of-the-art causal search algorithms in simulation, allowing efficient and accurate search even for dense graphs and graphs with more than 100 variables.

Causal discovery for observational sciences using supervised machine learning

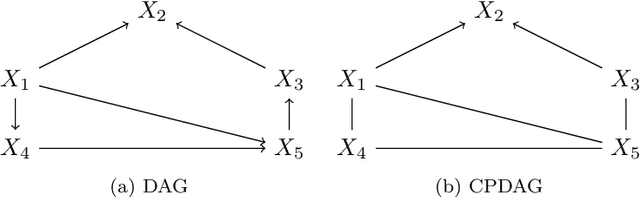
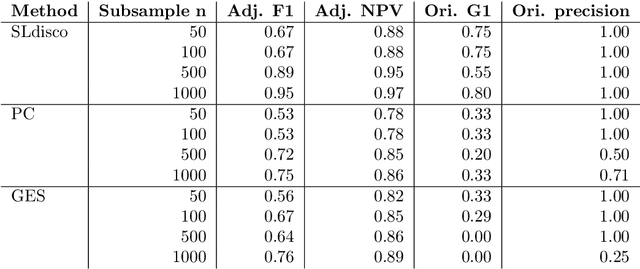
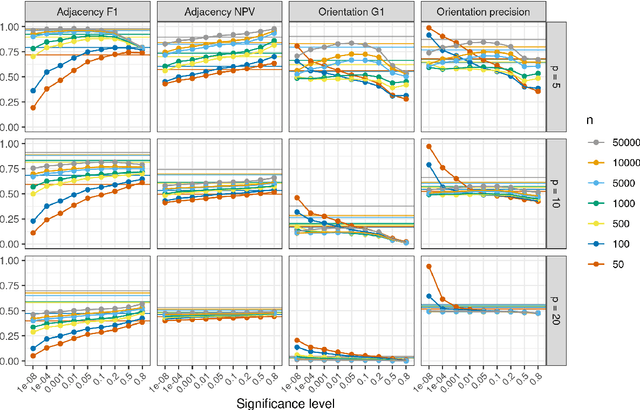
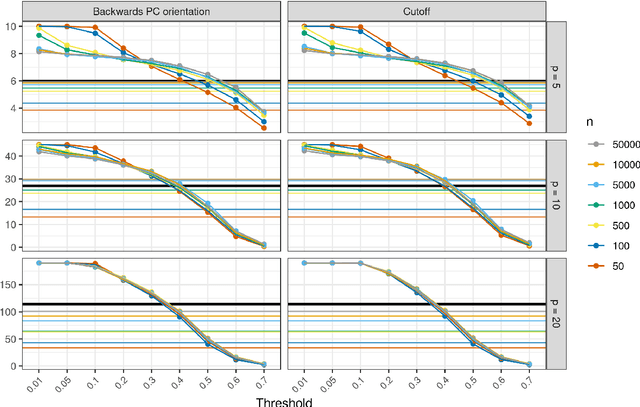
Causal inference can estimate causal effects, but unless data are collected experimentally, statistical analyses must rely on pre-specified causal models. Causal discovery algorithms are empirical methods for constructing such causal models from data. Several asymptotically correct methods already exist, but they generally struggle on smaller samples. Moreover, most methods focus on very sparse causal models, which may not always be a realistic representation of real-life data generating mechanisms. Finally, while causal relationships suggested by the methods often hold true, their claims about causal non-relatedness have high error rates. This non-conservative error tradeoff is not ideal for observational sciences, where the resulting model is directly used to inform causal inference: A causal model with many missing causal relations entails too strong assumptions and may lead to biased effect estimates. We propose a new causal discovery method that addresses these three shortcomings: Supervised learning discovery (SLdisco). SLdisco uses supervised machine learning to obtain a mapping from observational data to equivalence classes of causal models. We evaluate SLdisco in a large simulation study based on Gaussian data and we consider several choices of model size and sample size. We find that SLdisco is more conservative, only moderately less informative and less sensitive towards sample size than existing procedures. We furthermore provide a real epidemiological data application. We use random subsampling to investigate real data performance on small samples and again find that SLdisco is less sensitive towards sample size and hence seems to better utilize the information available in small datasets.

FRITL: A Hybrid Method for Causal Discovery in the Presence of Latent Confounders

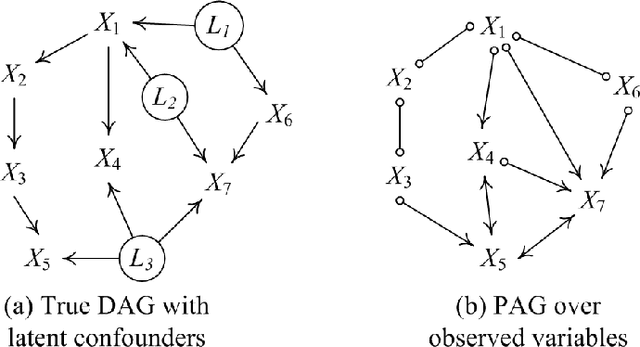
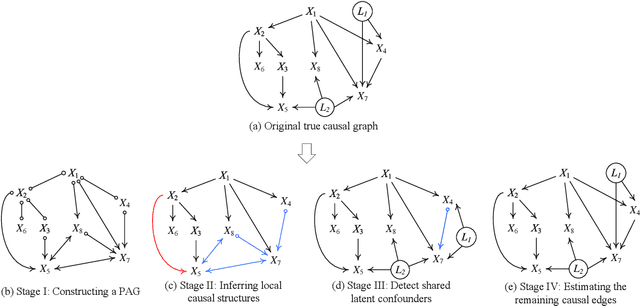
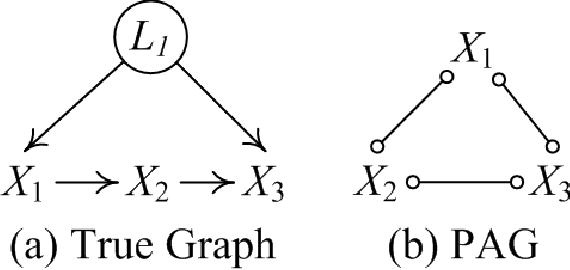
We consider the problem of estimating a particular type of linear non-Gaussian model. Without resorting to the overcomplete Independent Component Analysis (ICA), we show that under some mild assumptions, the model is uniquely identified by a hybrid method. Our method leverages the advantages of constraint-based methods and independent noise-based methods to handle both confounded and unconfounded situations. The first step of our method uses the FCI procedure, which allows confounders and is able to produce asymptotically correct results. The results, unfortunately, usually determine very few unconfounded direct causal relations, because whenever it is possible to have a confounder, it will indicate it. The second step of our procedure finds the unconfounded causal edges between observed variables among only those adjacent pairs informed by the FCI results. By making use of the so-called Triad condition, the third step is able to find confounders and their causal relations with other variables. Afterward, we apply ICA on a notably smaller set of graphs to identify remaining causal relationships if needed. Extensive experiments on simulated data and real-world data validate the correctness and effectiveness of the proposed method.

Causal Discovery from Heterogeneous/Nonstationary Data

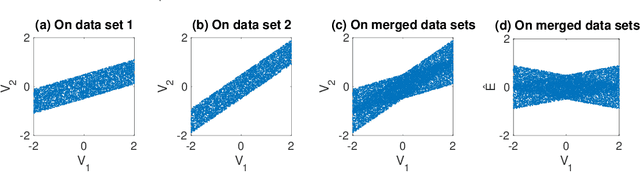
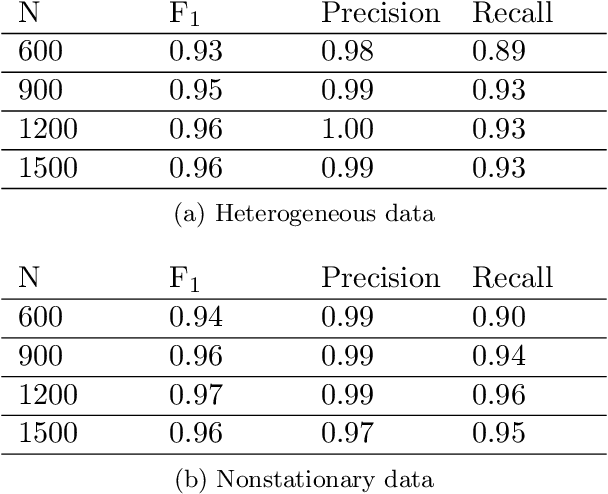
It is commonplace to encounter heterogeneous or nonstationary data, of which the underlying generating process changes across domains or over time. Such a distribution shift feature presents both challenges and opportunities for causal discovery. In this paper, we develop a framework for causal discovery from such data, called Constraint-based causal Discovery from heterogeneous/NOnstationary Data (CD-NOD), to find causal skeleton and directions and estimate the properties of mechanism changes. First, we propose an enhanced constraint-based procedure to detect variables whose local mechanisms change and recover the skeleton of the causal structure over observed variables. Second, we present a method to determine causal orientations by making use of independent changes in the data distribution implied by the underlying causal model, benefiting from information carried by changing distributions. After learning the causal structure, next, we investigate how to efficiently estimate the `driving force' of the nonstationarity of a causal mechanism. That is, we aim to extract from data a low-dimensional representation of changes. The proposed methods are nonparametric, with no hard restrictions on data distributions and causal mechanisms, and do not rely on window segmentation. Furthermore, we find that data heterogeneity benefits causal structure identification even with particular types of confounders. Finally, we show the connection between heterogeneity/nonstationarity and soft intervention in causal discovery. Experimental results on various synthetic and real-world data sets (task-fMRI and stock market data) are presented to demonstrate the efficacy of the proposed methods.

FASK with Interventional Knowledge Recovers Edges from the Sachs Model

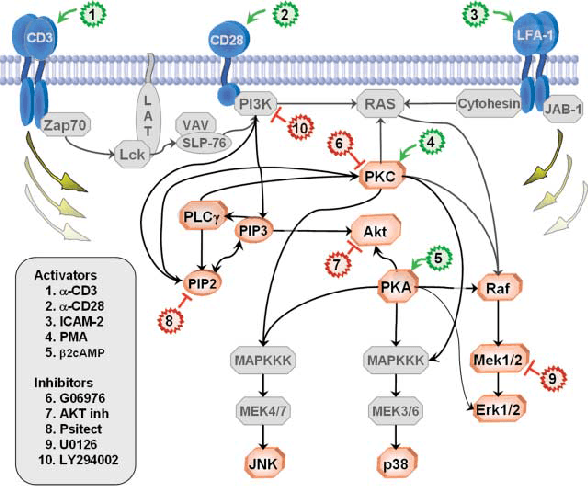
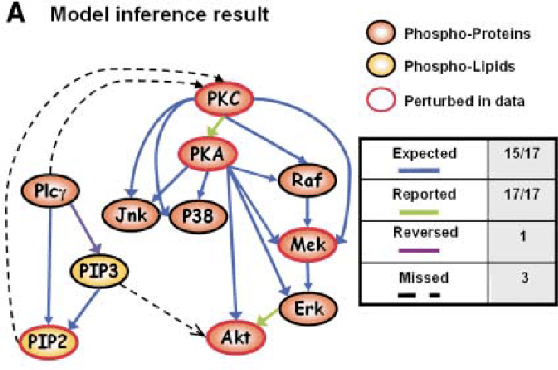
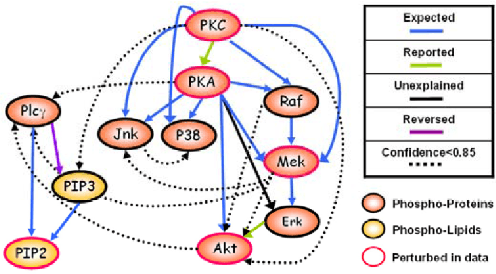
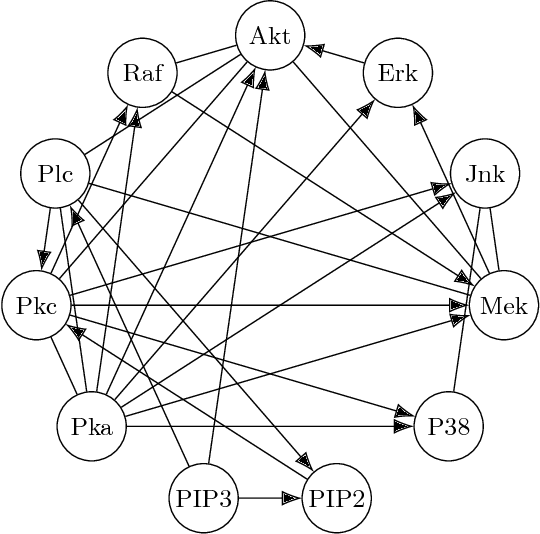
We report a procedure that, in one step from continuous data with minimal preparation, recovers the graph found by Sachs et al. \cite{sachs2005causal}, with only a few edges different. The algorithm, Fast Adjacency Skewness (FASK), relies on a mixture of linear reasoning and reasoning from the skewness of variables; the Sachs data is a good candidate for this procedure since the skewness of the variables is quite pronounced. We review the ground truth model from Sachs et al. as well as some of the fluctuations seen in the protein abundances in the system, give the Sachs model and the FASK model, and perform a detailed comparison. Some variation in hyper-parameters is explored, though the main result uses values at or near the defaults learned from work modeling fMRI data.

Causal Discovery in the Presence of Measurement Error: Identifiability Conditions

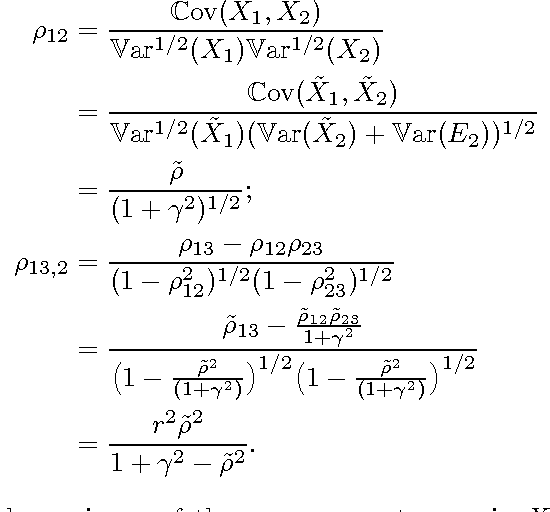
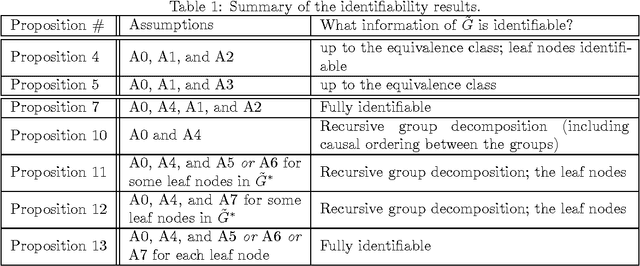
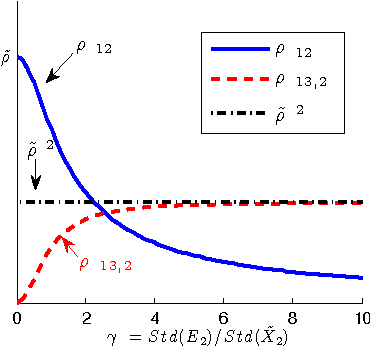
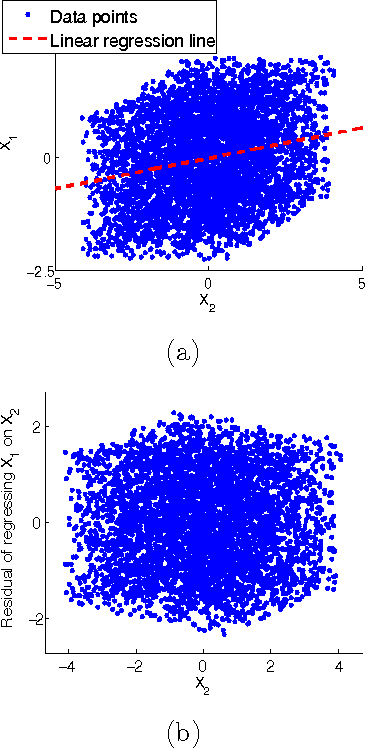
Measurement error in the observed values of the variables can greatly change the output of various causal discovery methods. This problem has received much attention in multiple fields, but it is not clear to what extent the causal model for the measurement-error-free variables can be identified in the presence of measurement error with unknown variance. In this paper, we study precise sufficient identifiability conditions for the measurement-error-free causal model and show what information of the causal model can be recovered from observed data. In particular, we present two different sets of identifiability conditions, based on the second-order statistics and higher-order statistics of the data, respectively. The former was inspired by the relationship between the generating model of the measurement-error-contaminated data and the factor analysis model, and the latter makes use of the identifiability result of the over-complete independent component analysis problem.