Long-Term Fairness Inquiries and Pursuits in Machine Learning: A Survey of Notions, Methods, and Challenges

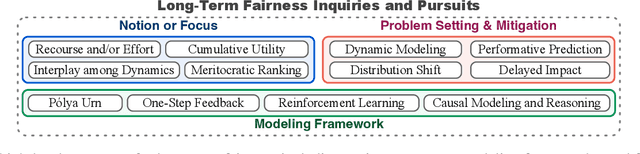
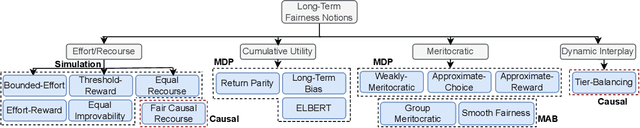
The widespread integration of Machine Learning systems in daily life, particularly in high-stakes domains, has raised concerns about the fairness implications. While prior works have investigated static fairness measures, recent studies reveal that automated decision-making has long-term implications and that off-the-shelf fairness approaches may not serve the purpose of achieving long-term fairness. Additionally, the existence of feedback loops and the interaction between models and the environment introduces additional complexities that may deviate from the initial fairness goals. In this survey, we review existing literature on long-term fairness from different perspectives and present a taxonomy for long-term fairness studies. We highlight key challenges and consider future research directions, analyzing both current issues and potential further explorations.

Fast Causal Inference with Non-Random Missingness by Test-Wise Deletion

Many real datasets contain values missing not at random (MNAR). In this scenario, investigators often perform list-wise deletion, or delete samples with any missing values, before applying causal discovery algorithms. List-wise deletion is a sound and general strategy when paired with algorithms such as FCI and RFCI, but the deletion procedure also eliminates otherwise good samples that contain only a few missing values. In this report, we show that we can more efficiently utilize the observed values with test-wise deletion while still maintaining algorithmic soundness. Here, test-wise deletion refers to the process of list-wise deleting samples only among the variables required for each conditional independence (CI) test used in constraint-based searches. Test-wise deletion therefore often saves more samples than list-wise deletion for each CI test, especially when we have a sparse underlying graph. Our theoretical results show that test-wise deletion is sound under the justifiable assumption that none of the missingness mechanisms causally affect each other in the underlying causal graph. We also find that FCI and RFCI with test-wise deletion outperform their list-wise deletion and imputation counterparts on average when MNAR holds in both synthetic and real data.

Estimating and Controlling the False Discovery Rate for the PC Algorithm Using Edge-Specific P-Values

The PC algorithm allows investigators to estimate a complete partially directed acyclic graph (CPDAG) from a finite dataset, but few groups have investigated strategies for estimating and controlling the false discovery rate (FDR) of the edges in the CPDAG. In this paper, we introduce PC with p-values (PC-p), a fast algorithm which robustly computes edge-specific p-values and then estimates and controls the FDR across the edges. PC-p specifically uses the p-values returned by many conditional independence tests to upper bound the p-values of more complex edge-specific hypothesis tests. The algorithm then estimates and controls the FDR using the bounded p-values and the Benjamini-Yekutieli FDR procedure. Modifications to the original PC algorithm also help PC-p accurately compute the upper bounds despite non-zero Type II error rates. Experiments show that PC-p yields more accurate FDR estimation and control across the edges in a variety of CPDAGs compared to alternative methods.

Calculation of Entailed Rank Constraints in Partially Non-Linear and Cyclic Models

The Trek Separation Theorem (Sullivant et al. 2010) states necessary and sufficient conditions for a linear directed acyclic graphical model to entail for all possible values of its linear coefficients that the rank of various sub-matrices of the covariance matrix is less than or equal to n, for any given n. In this paper, I extend the Trek Separation Theorem in two ways: I prove that the same necessary and sufficient conditions apply even when the generating model is partially non-linear and contains some cycles. This justifies application of constraint-based causal search algorithms such as the BuildPureClusters algorithm (Silva et al. 2006) for discovering the causal structure of latent variable models to data generated by a wider class of causal models that may contain non-linear and cyclic relations among the latent variables.

Detecting Causal Relations in the Presence of Unmeasured Variables

The presence of latent variables can greatly complicate inferences about causal relations between measured variables from statistical data. In many cases, the presence of latent variables makes it impossible to determine for two measured variables A and B, whether A causes B, B causes A, or there is some common cause. In this paper I present several theorems that state conditions under which it is possible to reliably infer the causal relation between two measured variables, regardless of whether latent variables are acting or not.

Causal Inference in the Presence of Latent Variables and Selection Bias

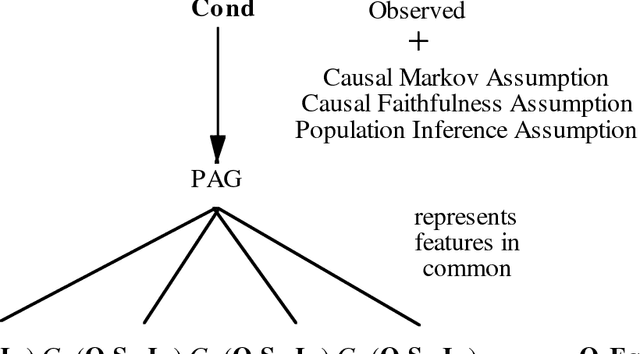
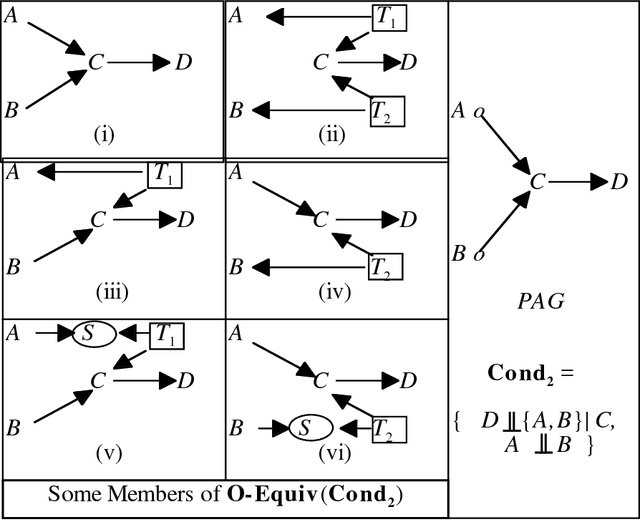
We show that there is a general, informative and reliable procedure for discovering causal relations when, for all the investigator knows, both latent variables and selection bias may be at work. Given information about conditional independence and dependence relations between measured variables, even when latent variables and selection bias may be present, there are sufficient conditions for reliably concluding that there is a causal path from one variable to another, and sufficient conditions for reliably concluding when no such causal path exists.

Directed Cyclic Graphical Representations of Feedback Models

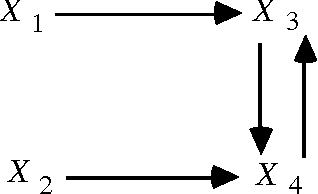
The use of directed acyclic graphs (DAGs) to represent conditional independence relations among random variables has proved fruitful in a variety of ways. Recursive structural equation models are one kind of DAG model. However, non-recursive structural equation models of the kinds used to model economic processes are naturally represented by directed cyclic graphs with independent errors, a characterization of conditional independence errors, a characterization of conditional independence constraints is obtained, and it is shown that the result generalizes in a natural way to systems in which the error variables or noises are statistically dependent. For non-linear systems with independent errors a sufficient condition for conditional independence of variables in associated distributions is obtained.

Semi-Instrumental Variables: A Test for Instrument Admissibility

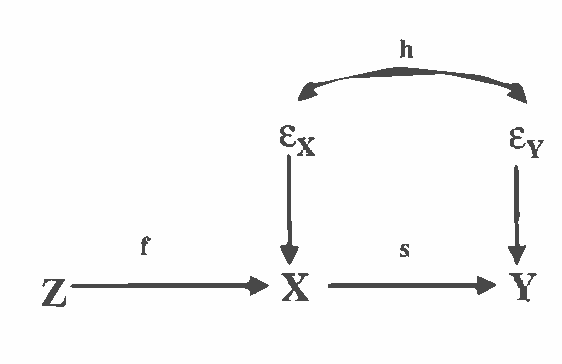
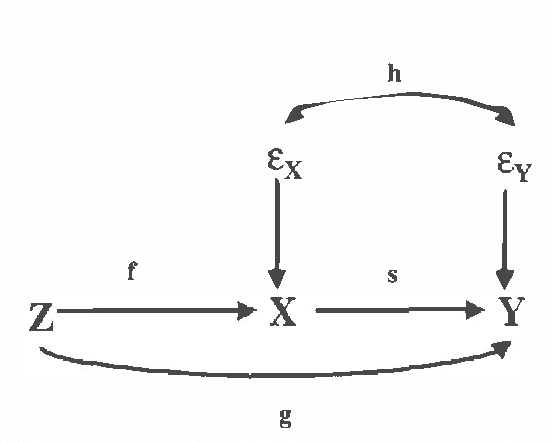
In a causal graphical model, an instrument for a variable X and its effect Y is a random variable that is a cause of X and independent of all the causes of Y except X. (Pearl (1995), Spirtes et al (2000)). Instrumental variables can be used to estimate how the distribution of an effect will respond to a manipulation of its causes, even in the presence of unmeasured common causes (confounders). In typical instrumental variable estimation, instruments are chosen based on domain knowledge. There is currently no statistical test for validating a variable as an instrument. In this paper, we introduce the concept of semi-instrument, which generalizes the concept of instrument. We show that in the framework of additive models, under certain conditions, we can test whether a variable is semi-instrumental. Moreover, adding some distribution assumptions, we can test whether two semi-instruments are instrumental. We give algorithms to estimate the p-value that a random variable is semi-instrumental, and the p-value that two semi-instruments are both instrumental. These algorithms can be used to test the experts' choice of instruments, or to identify instruments automatically.

Strong Faithfulness and Uniform Consistency in Causal Inference

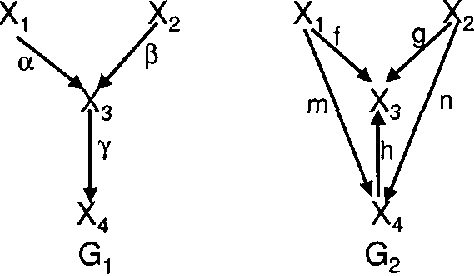
A fundamental question in causal inference is whether it is possible to reliably infer manipulation effects from observational data. There are a variety of senses of asymptotic reliability in the statistical literature, among which the most commonly discussed frequentist notions are pointwise consistency and uniform consistency. Uniform consistency is in general preferred to pointwise consistency because the former allows us to control the worst case error bounds with a finite sample size. In the sense of pointwise consistency, several reliable causal inference algorithms have been established under the Markov and Faithfulness assumptions [Pearl 2000, Spirtes et al. 2001]. In the sense of uniform consistency, however, reliable causal inference is impossible under the two assumptions when time order is unknown and/or latent confounders are present [Robins et al. 2000]. In this paper we present two natural generalizations of the Faithfulness assumption in the context of structural equation models, under which we show that the typical algorithms in the literature (in some cases with modifications) are uniformly consistent even when the time order is unknown. We also discuss the situation where latent confounders may be present and the sense in which the Faithfulness assumption is a limiting case of the stronger assumptions.

Learning Measurement Models for Unobserved Variables

Observed associations in a database may be due in whole or part to variations in unrecorded (latent) variables. Identifying such variables and their causal relationships with one another is a principal goal in many scientific and practical domains. Previous work shows that, given a partition of observed variables such that members of a class share only a single latent common cause, standard search algorithms for causal Bayes nets can infer structural relations between latent variables. We introduce an algorithm for discovering such partitions when they exist. Uniquely among available procedures, the algorithm is (asymptotically) correct under standard assumptions in causal Bayes net search algorithms, requires no prior knowledge of the number of latent variables, and does not depend on the mathematical form of the relationships among the latent variables. We evaluate the algorithm on a variety of simulated data sets.