Dual Risk Minimization: Towards Next-Level Robustness in Fine-tuning Zero-Shot Models

Fine-tuning foundation models often compromises their robustness to distribution shifts. To remedy this, most robust fine-tuning methods aim to preserve the pre-trained features. However, not all pre-trained features are robust and those methods are largely indifferent to which ones to preserve. We propose dual risk minimization (DRM), which combines empirical risk minimization with worst-case risk minimization, to better preserve the core features of downstream tasks. In particular, we utilize core-feature descriptions generated by LLMs to induce core-based zero-shot predictions which then serve as proxies to estimate the worst-case risk. DRM balances two crucial aspects of model robustness: expected performance and worst-case performance, establishing a new state of the art on various real-world benchmarks. DRM significantly improves the out-of-distribution performance of CLIP ViT-L/14@336 on ImageNet (75.9 to 77.1), WILDS-iWildCam (47.1 to 51.8), and WILDS-FMoW (50.7 to 53.1); opening up new avenues for robust fine-tuning. Our code is available at https://github.com/vaynexie/DRM .

Structured Learning of Compositional Sequential Interventions

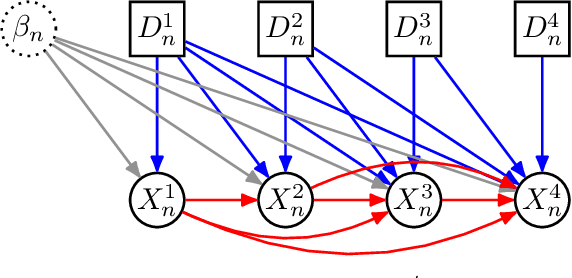
We consider sequential treatment regimes where each unit is exposed to combinations of interventions over time. When interventions are described by qualitative labels, such as ``close schools for a month due to a pandemic'' or ``promote this podcast to this user during this week'', it is unclear which appropriate structural assumptions allow us to generalize behavioral predictions to previously unseen combinatorial sequences. Standard black-box approaches mapping sequences of categorical variables to outputs are applicable, but they rely on poorly understood assumptions on how reliable generalization can be obtained, and may underperform under sparse sequences, temporal variability, and large action spaces. To approach that, we pose an explicit model for \emph{composition}, that is, how the effect of sequential interventions can be isolated into modules, clarifying which data conditions allow for the identification of their combined effect at different units and time steps. We show the identification properties of our compositional model, inspired by advances in causal matrix factorization methods but focusing on predictive models for novel compositions of interventions instead of matrix completion tasks and causal effect estimation. We compare our approach to flexible but generic black-box models to illustrate how structure aids prediction in sparse data conditions.

Bounding Causal Effects with Leaky Instruments

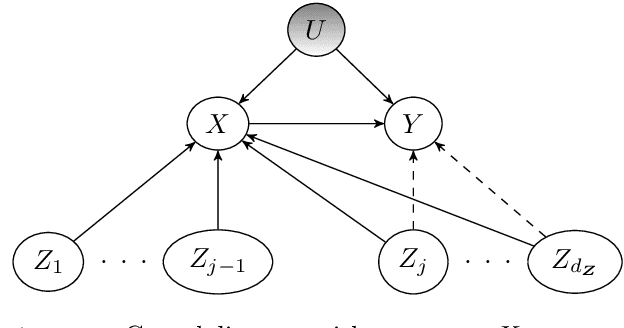
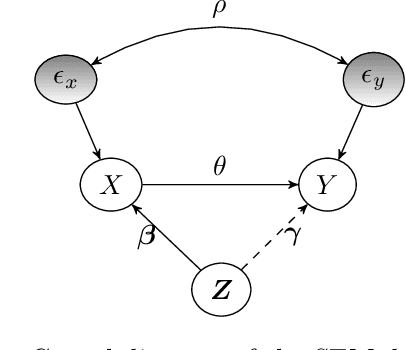
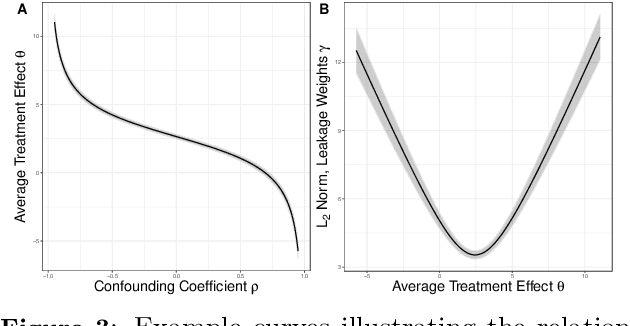
Instrumental variables (IVs) are a popular and powerful tool for estimating causal effects in the presence of unobserved confounding. However, classical approaches rely on strong assumptions such as the $\textit{exclusion criterion}$, which states that instrumental effects must be entirely mediated by treatments. This assumption often fails in practice. When IV methods are improperly applied to data that do not meet the exclusion criterion, estimated causal effects may be badly biased. In this work, we propose a novel solution that provides $\textit{partial}$ identification in linear models given a set of $\textit{leaky instruments}$, which are allowed to violate the exclusion criterion to some limited degree. We derive a convex optimization objective that provides provably sharp bounds on the average treatment effect under some common forms of information leakage, and implement inference procedures to quantify the uncertainty of resulting estimates. We demonstrate our method in a set of experiments with simulated data, where it performs favorably against the state of the art.

Counterfactual Fairness Is Not Demographic Parity, and Other Observations

Blanket statements of equivalence between causal concepts and purely probabilistic concepts should be approached with care. In this short note, I examine a recent claim that counterfactual fairness is equivalent to demographic parity. The claim fails to hold up upon closer examination. I will take the opportunity to address some broader misunderstandings about counterfactual fairness.

Intervention Generalization: A View from Factor Graph Models

One of the goals of causal inference is to generalize from past experiments and observational data to novel conditions. While it is in principle possible to eventually learn a mapping from a novel experimental condition to an outcome of interest, provided a sufficient variety of experiments is available in the training data, coping with a large combinatorial space of possible interventions is hard. Under a typical sparse experimental design, this mapping is ill-posed without relying on heavy regularization or prior distributions. Such assumptions may or may not be reliable, and can be hard to defend or test. In this paper, we take a close look at how to warrant a leap from past experiments to novel conditions based on minimal assumptions about the factorization of the distribution of the manipulated system, communicated in the well-understood language of factor graph models. A postulated $\textit{interventional factor model}$ (IFM) may not always be informative, but it conveniently abstracts away a need for explicit unmeasured confounding and feedback mechanisms, leading to directly testable claims. We derive necessary and sufficient conditions for causal effect identifiability with IFMs using data from a collection of experimental settings, and implement practical algorithms for generalizing expected outcomes to novel conditions never observed in the data.

Spawrious: A Benchmark for Fine Control of Spurious Correlation Biases

The problem of spurious correlations (SCs) arises when a classifier relies on non-predictive features that happen to be correlated with the labels in the training data. For example, a classifier may misclassify dog breeds based on the background of dog images. This happens when the backgrounds are correlated with other breeds in the training data, leading to misclassifications during test time. Previous SC benchmark datasets suffer from varying issues, e.g., over-saturation or only containing one-to-one (O2O) SCs, but no many-to-many (M2M) SCs arising between groups of spurious attributes and classes. In this paper, we present Spawrious-{O2O, M2M}-{Easy, Medium, Hard}, an image classification benchmark suite containing spurious correlations among different dog breeds and background locations. To create this dataset, we employ a text-to-image model to generate photo-realistic images, and an image captioning model to filter out unsuitable ones. The resulting dataset is of high quality, containing approximately 152,000 images. Our experimental results demonstrate that state-of-the-art group robustness methods struggle with Spawrious, most notably on the Hard-splits with $<60\%$ accuracy. By examining model misclassifications, we detect reliances on spurious backgrounds, demonstrating that our dataset provides a significant challenge to drive future research.

Pragmatic Fairness: Developing Policies with Outcome Disparity Control

We introduce a causal framework for designing optimal policies that satisfy fairness constraints. We take a pragmatic approach asking what we can do with an action space available to us and only with access to historical data. We propose two different fairness constraints: a moderation breaking constraint which aims at blocking moderation paths from the action and sensitive attribute to the outcome, and by that at reducing disparity in outcome levels as much as the provided action space permits; and an equal benefit constraint which aims at distributing gain from the new and maximized policy equally across sensitive attribute levels, and thus at keeping pre-existing preferential treatment in place or avoiding the introduction of new disparity. We introduce practical methods for implementing the constraints and illustrate their uses on experiments with semi-synthetic models.

Causal Machine Learning: A Survey and Open Problems

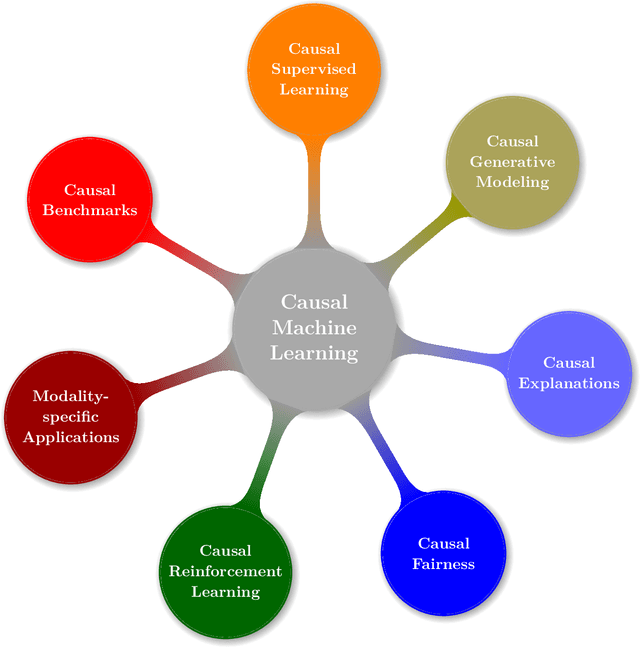
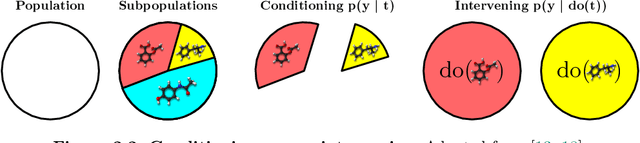
Causal Machine Learning (CausalML) is an umbrella term for machine learning methods that formalize the data-generation process as a structural causal model (SCM). This allows one to reason about the effects of changes to this process (i.e., interventions) and what would have happened in hindsight (i.e., counterfactuals). We categorize work in \causalml into five groups according to the problems they tackle: (1) causal supervised learning, (2) causal generative modeling, (3) causal explanations, (4) causal fairness, (5) causal reinforcement learning. For each category, we systematically compare its methods and point out open problems. Further, we review modality-specific applications in computer vision, natural language processing, and graph representation learning. Finally, we provide an overview of causal benchmarks and a critical discussion of the state of this nascent field, including recommendations for future work.

Causal Inference with Treatment Measurement Error: A Nonparametric Instrumental Variable Approach

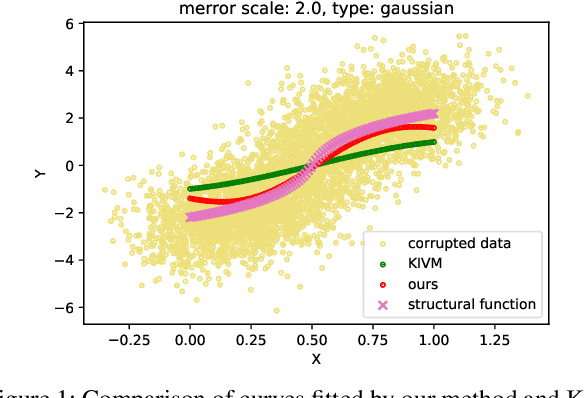
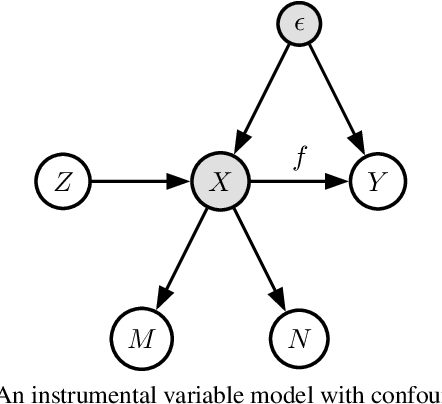
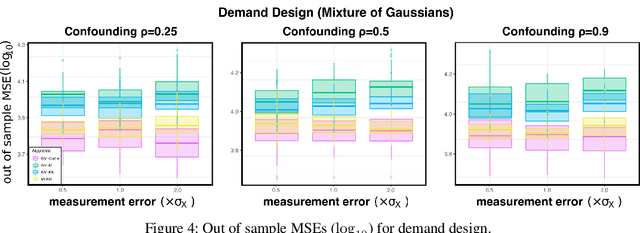
We propose a kernel-based nonparametric estimator for the causal effect when the cause is corrupted by error. We do so by generalizing estimation in the instrumental variable setting. Despite significant work on regression with measurement error, additionally handling unobserved confounding in the continuous setting is non-trivial: we have seen little prior work. As a by-product of our investigation, we clarify a connection between mean embeddings and characteristic functions, and how learning one simultaneously allows one to learn the other. This opens the way for kernel method research to leverage existing results in characteristic function estimation. Finally, we empirically show that our proposed method, MEKIV, improves over baselines and is robust under changes in the strength of measurement error and to the type of error distributions.

FCN-Pose: A Pruned and Quantized CNN for Robot Pose Estimation for Constrained Devices

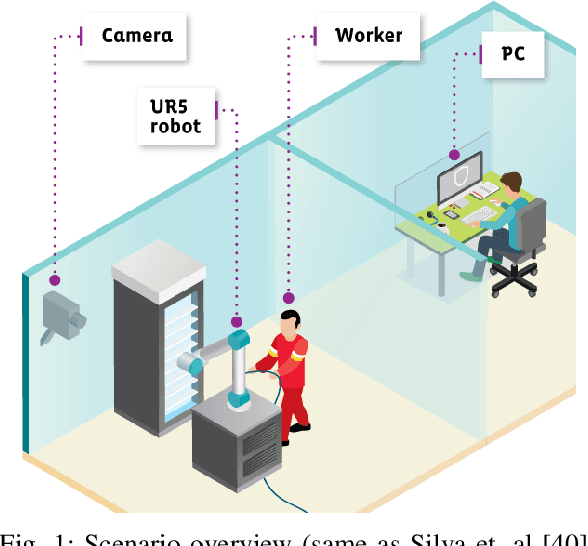
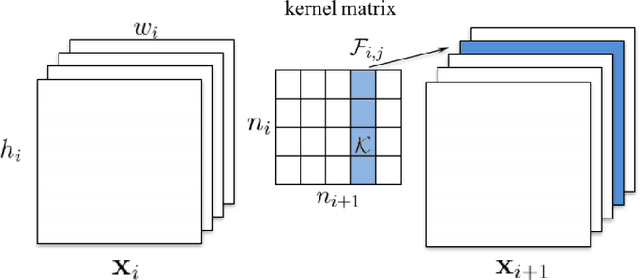
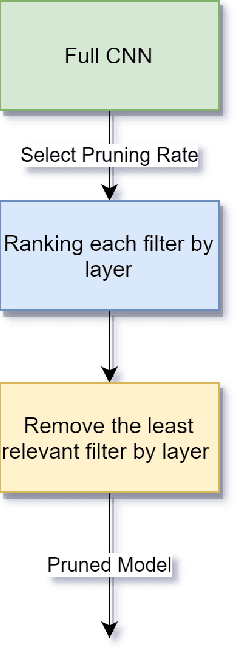
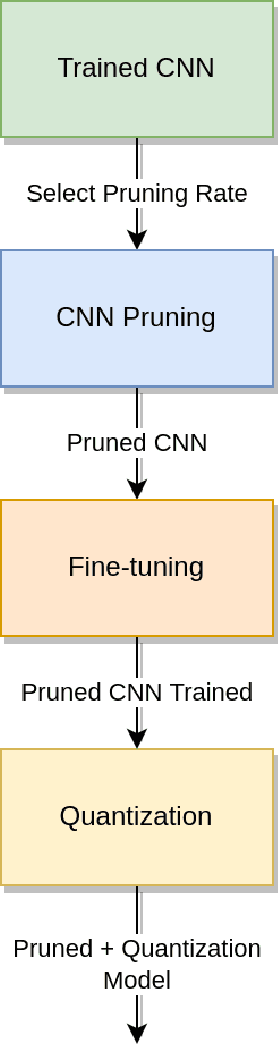
IoT devices suffer from resource limitations, such as processor, RAM, and disc storage. These limitations become more evident when handling demanding applications, such as deep learning, well-known for their heavy computational requirements. A case in point is robot pose estimation, an application that predicts the critical points of the desired image object. One way to mitigate processing and storage problems is compressing that deep learning application. This paper proposes a new CNN for the pose estimation while applying the compression techniques of pruning and quantization to reduce his demands and improve the response time. While the pruning process reduces the total number of parameters required for inference, quantization decreases the precision of the floating-point. We run the approach using a pose estimation task for a robotic arm and compare the results in a high-end device and a constrained device. As metrics, we consider the number of Floating-point Operations Per Second(FLOPS), the total of mathematical computations, the calculation of parameters, the inference time, and the number of video frames processed per second. In addition, we undertake a qualitative evaluation where we compare the output image predicted for each pruned network with the corresponding original one. We reduce the originally proposed network to a 70% pruning rate, implying an 88.86% reduction in parameters, 94.45% reduction in FLOPS, and for the disc storage, we reduced the requirement in 70% while increasing error by a mere $1\%$. With regard input image processing, this metric increases from 11.71 FPS to 41.9 FPS for the Desktop case. When using the constrained device, image processing augmented from 2.86 FPS to 10.04 FPS. The higher processing rate of image frames achieved by the proposed approach allows a much shorter response time.