Bounding Causal Effects with Leaky Instruments

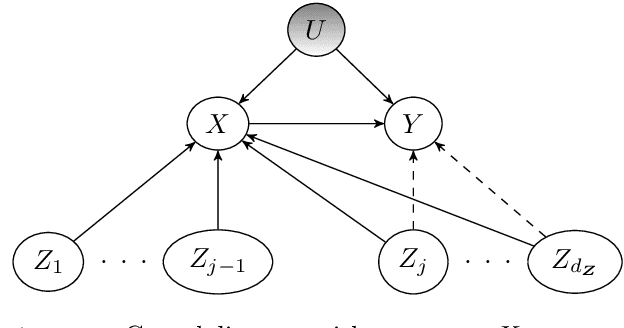
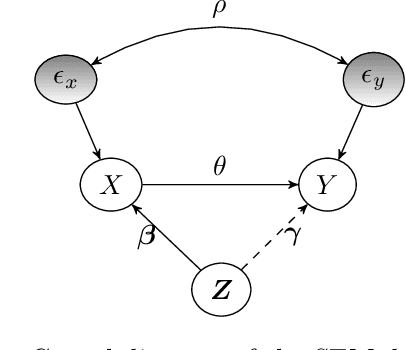
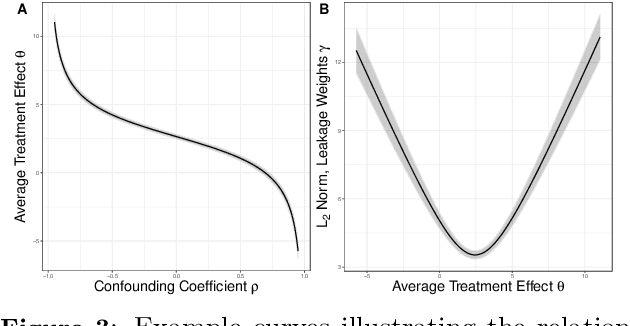
Instrumental variables (IVs) are a popular and powerful tool for estimating causal effects in the presence of unobserved confounding. However, classical approaches rely on strong assumptions such as the $\textit{exclusion criterion}$, which states that instrumental effects must be entirely mediated by treatments. This assumption often fails in practice. When IV methods are improperly applied to data that do not meet the exclusion criterion, estimated causal effects may be badly biased. In this work, we propose a novel solution that provides $\textit{partial}$ identification in linear models given a set of $\textit{leaky instruments}$, which are allowed to violate the exclusion criterion to some limited degree. We derive a convex optimization objective that provides provably sharp bounds on the average treatment effect under some common forms of information leakage, and implement inference procedures to quantify the uncertainty of resulting estimates. We demonstrate our method in a set of experiments with simulated data, where it performs favorably against the state of the art.

Quantifying Human Priors over Social and Navigation Networks

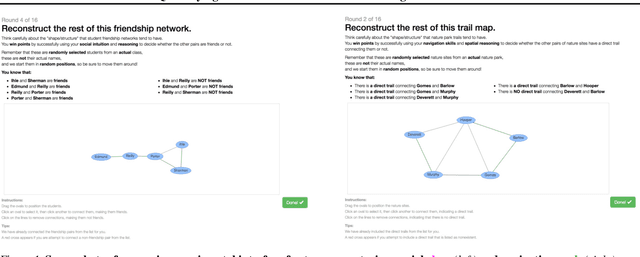
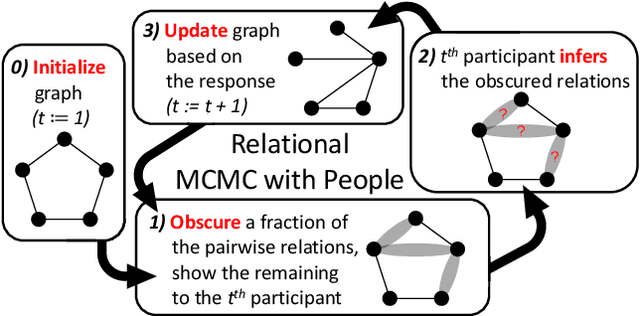
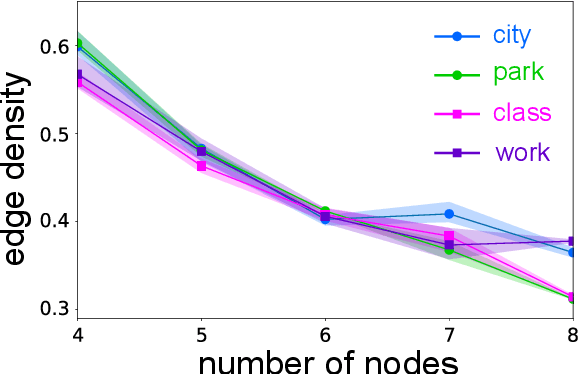
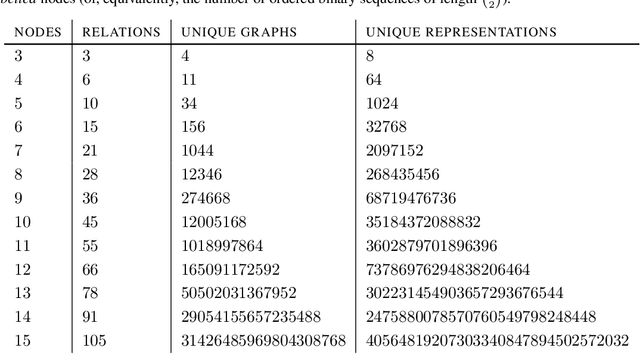
Human knowledge is largely implicit and relational -- do we have a friend in common? can I walk from here to there? In this work, we leverage the combinatorial structure of graphs to quantify human priors over such relational data. Our experiments focus on two domains that have been continuously relevant over evolutionary timescales: social interaction and spatial navigation. We find that some features of the inferred priors are remarkably consistent, such as the tendency for sparsity as a function of graph size. Other features are domain-specific, such as the propensity for triadic closure in social interactions. More broadly, our work demonstrates how nonclassical statistical analysis of indirect behavioral experiments can be used to efficiently model latent biases in the data.

Intervention Generalization: A View from Factor Graph Models

One of the goals of causal inference is to generalize from past experiments and observational data to novel conditions. While it is in principle possible to eventually learn a mapping from a novel experimental condition to an outcome of interest, provided a sufficient variety of experiments is available in the training data, coping with a large combinatorial space of possible interventions is hard. Under a typical sparse experimental design, this mapping is ill-posed without relying on heavy regularization or prior distributions. Such assumptions may or may not be reliable, and can be hard to defend or test. In this paper, we take a close look at how to warrant a leap from past experiments to novel conditions based on minimal assumptions about the factorization of the distribution of the manipulated system, communicated in the well-understood language of factor graph models. A postulated $\textit{interventional factor model}$ (IFM) may not always be informative, but it conveniently abstracts away a need for explicit unmeasured confounding and feedback mechanisms, leading to directly testable claims. We derive necessary and sufficient conditions for causal effect identifiability with IFMs using data from a collection of experimental settings, and implement practical algorithms for generalizing expected outcomes to novel conditions never observed in the data.

Private and Communication-Efficient Algorithms for Entropy Estimation

Modern statistical estimation is often performed in a distributed setting where each sample belongs to a single user who shares their data with a central server. Users are typically concerned with preserving the privacy of their samples, and also with minimizing the amount of data they must transmit to the server. We give improved private and communication-efficient algorithms for estimating several popular measures of the entropy of a distribution. All of our algorithms have constant communication cost and satisfy local differential privacy. For a joint distribution over many variables whose conditional independence is given by a tree, we describe algorithms for estimating Shannon entropy that require a number of samples that is linear in the number of variables, compared to the quadratic sample complexity of prior work. We also describe an algorithm for estimating Gini entropy whose sample complexity has no dependence on the support size of the distribution and can be implemented using a single round of concurrent communication between the users and the server. In contrast, the previously best-known algorithm has high communication cost and requires the server to facilitate interaction between the users. Finally, we describe an algorithm for estimating collision entropy that generalizes the best known algorithm to the private and communication-efficient setting.