Bounding Causal Effects with Leaky Instruments

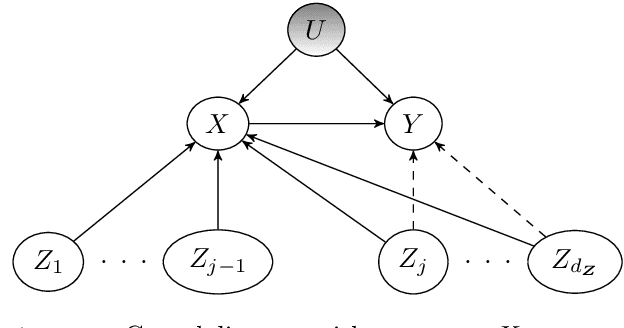
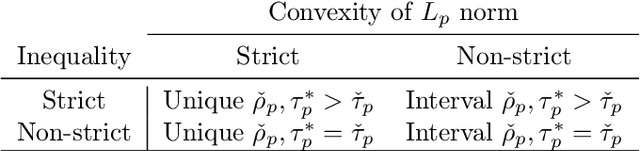
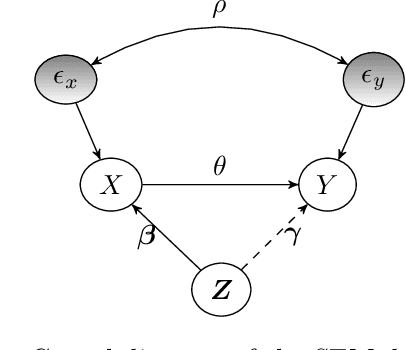
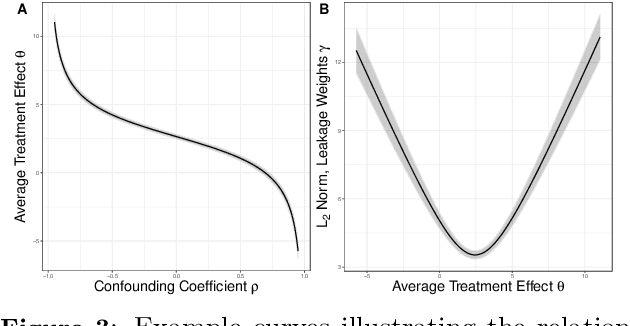
Instrumental variables (IVs) are a popular and powerful tool for estimating causal effects in the presence of unobserved confounding. However, classical approaches rely on strong assumptions such as the $\textit{exclusion criterion}$, which states that instrumental effects must be entirely mediated by treatments. This assumption often fails in practice. When IV methods are improperly applied to data that do not meet the exclusion criterion, estimated causal effects may be badly biased. In this work, we propose a novel solution that provides $\textit{partial}$ identification in linear models given a set of $\textit{leaky instruments}$, which are allowed to violate the exclusion criterion to some limited degree. We derive a convex optimization objective that provides provably sharp bounds on the average treatment effect under some common forms of information leakage, and implement inference procedures to quantify the uncertainty of resulting estimates. We demonstrate our method in a set of experiments with simulated data, where it performs favorably against the state of the art.

Algorithmic Recourse in Partially and Fully Confounded Settings Through Bounding Counterfactual Effects

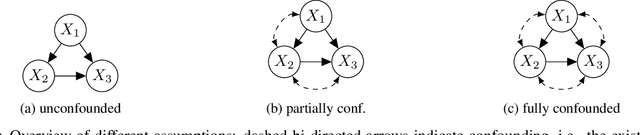
Algorithmic recourse aims to provide actionable recommendations to individuals to obtain a more favourable outcome from an automated decision-making system. As it involves reasoning about interventions performed in the physical world, recourse is fundamentally a causal problem. Existing methods compute the effect of recourse actions using a causal model learnt from data under the assumption of no hidden confounding and modelling assumptions such as additive noise. Building on the seminal work of Balke and Pearl (1994), we propose an alternative approach for discrete random variables which relaxes these assumptions and allows for unobserved confounding and arbitrary structural equations. The proposed approach only requires specification of the causal graph and confounding structure and bounds the expected counterfactual effect of recourse actions. If the lower bound is above a certain threshold, i.e., on the other side of the decision boundary, recourse is guaranteed in expectation.

Proximal Causal Learning with Kernels: Two-Stage Estimation and Moment Restriction

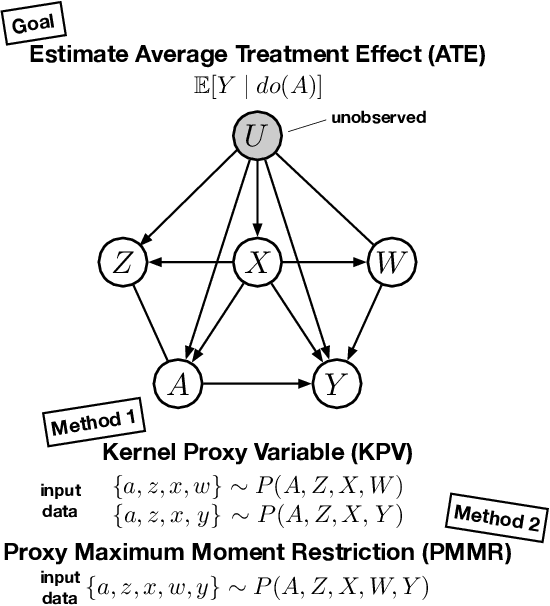
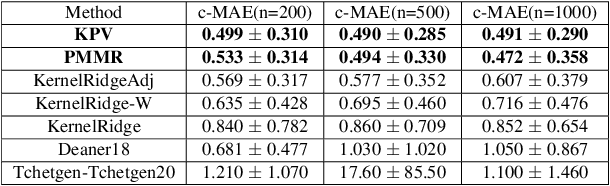
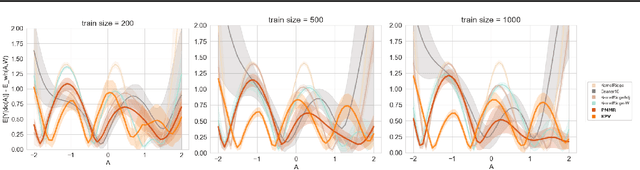
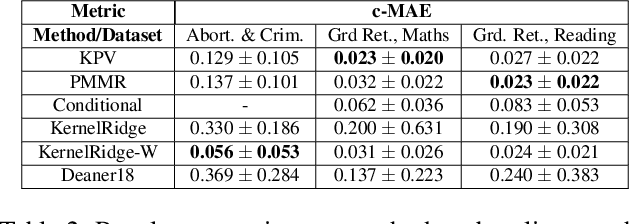
We address the problem of causal effect estimation in the presence of unobserved confounding, but where proxies for the latent confounder(s) are observed. We propose two kernel-based methods for nonlinear causal effect estimation in this setting: (a) a two-stage regression approach, and (b) a maximum moment restriction approach. We focus on the proximal causal learning setting, but our methods can be used to solve a wider class of inverse problems characterised by a Fredholm integral equation. In particular, we provide a unifying view of two-stage and moment restriction approaches for solving this problem in a nonlinear setting. We provide consistency guarantees for each algorithm, and we demonstrate these approaches achieve competitive results on synthetic data and data simulating a real-world task. In particular, our approach outperforms earlier methods that are not suited to leveraging proxy variables.