Yuchen Zhu
College of Pharmaceutical Sciences and Cancer Center, Zhejiang University
From Masks to Worlds: A Hitchhiker's Guide to World Models
Oct 23, 2025Abstract:This is not a typical survey of world models; it is a guide for those who want to build worlds. We do not aim to catalog every paper that has ever mentioned a ``world model". Instead, we follow one clear road: from early masked models that unified representation learning across modalities, to unified architectures that share a single paradigm, then to interactive generative models that close the action-perception loop, and finally to memory-augmented systems that sustain consistent worlds over time. We bypass loosely related branches to focus on the core: the generative heart, the interactive loop, and the memory system. We show that this is the most promising path towards true world models.
Millisecond-Response Tracking and Gazing System for UAVs: A Domestic Solution Based on "Phytium + Cambricon"
Sep 04, 2025Abstract:In the frontier research and application of current video surveillance technology, traditional camera systems exhibit significant limitations of response delay exceeding 200 ms in dynamic scenarios due to the insufficient deep feature extraction capability of automatic recognition algorithms and the efficiency bottleneck of computing architectures, failing to meet the real-time requirements in complex scenes. To address this issue, this study proposes a heterogeneous computing architecture based on Phytium processors and Cambricon accelerator cards, constructing a UAV tracking and gazing system with millisecond-level response capability. At the hardware level, the system adopts a collaborative computing architecture of Phytium FT-2000/4 processors and MLU220 accelerator cards, enhancing computing power through multi-card parallelism. At the software level, it innovatively integrates a lightweight YOLOv5s detection network with a DeepSORT cascaded tracking algorithm, forming a closed-loop control chain of "detection-tracking-feedback". Experimental results demonstrate that the system achieves a stable single-frame comprehensive processing delay of 50-100 ms in 1920*1080 resolution video stream processing, with a multi-scale target recognition accuracy of over 98.5%, featuring both low latency and high precision. This study provides an innovative solution for UAV monitoring and the application of domestic chips.
Rethinking Query-based Transformer for Continual Image Segmentation
Jul 10, 2025Abstract:Class-incremental/Continual image segmentation (CIS) aims to train an image segmenter in stages, where the set of available categories differs at each stage. To leverage the built-in objectness of query-based transformers, which mitigates catastrophic forgetting of mask proposals, current methods often decouple mask generation from the continual learning process. This study, however, identifies two key issues with decoupled frameworks: loss of plasticity and heavy reliance on input data order. To address these, we conduct an in-depth investigation of the built-in objectness and find that highly aggregated image features provide a shortcut for queries to generate masks through simple feature alignment. Based on this, we propose SimCIS, a simple yet powerful baseline for CIS. Its core idea is to directly select image features for query assignment, ensuring "perfect alignment" to preserve objectness, while simultaneously allowing queries to select new classes to promote plasticity. To further combat catastrophic forgetting of categories, we introduce cross-stage consistency in selection and an innovative "visual query"-based replay mechanism. Experiments demonstrate that SimCIS consistently outperforms state-of-the-art methods across various segmentation tasks, settings, splits, and input data orders. All models and codes will be made publicly available at https://github.com/SooLab/SimCIS.
Diffuse Everything: Multimodal Diffusion Models on Arbitrary State Spaces
Jun 09, 2025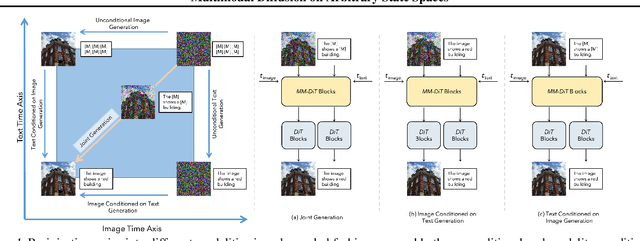
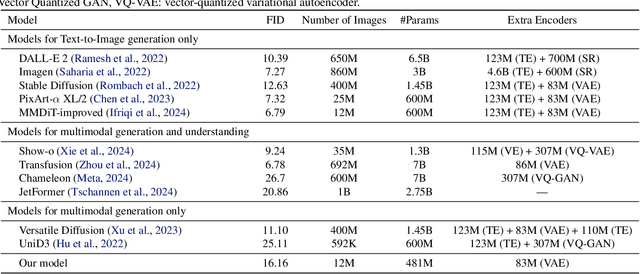
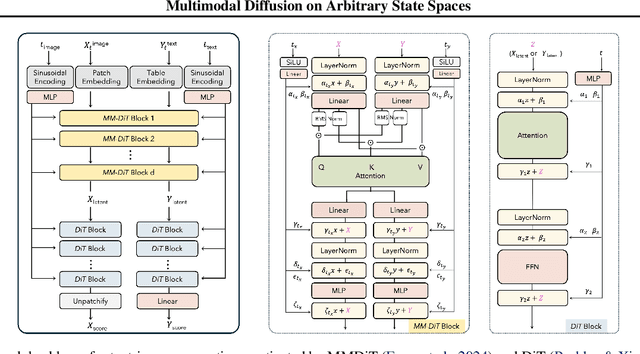
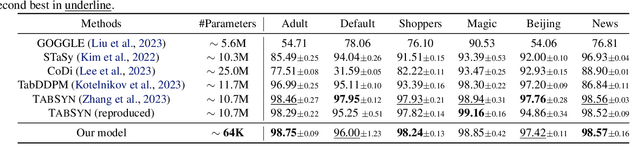
Abstract:Diffusion models have demonstrated remarkable performance in generating unimodal data across various tasks, including image, video, and text generation. On the contrary, the joint generation of multimodal data through diffusion models is still in the early stages of exploration. Existing approaches heavily rely on external preprocessing protocols, such as tokenizers and variational autoencoders, to harmonize varied data representations into a unified, unimodal format. This process heavily demands the high accuracy of encoders and decoders, which can be problematic for applications with limited data. To lift this restriction, we propose a novel framework for building multimodal diffusion models on arbitrary state spaces, enabling native generation of coupled data across different modalities. By introducing an innovative decoupled noise schedule for each modality, we enable both unconditional and modality-conditioned generation within a single model simultaneously. We empirically validate our approach for text-image generation and mixed-type tabular data synthesis, demonstrating that it achieves competitive performance.
Mimicking or Reasoning: Rethinking Multi-Modal In-Context Learning in Vision-Language Models
Jun 09, 2025Abstract:Vision-language models (VLMs) are widely assumed to exhibit in-context learning (ICL), a property similar to that of their language-only counterparts. While recent work suggests VLMs can perform multimodal ICL (MM-ICL), studies show they often rely on shallow heuristics -- such as copying or majority voting -- rather than true task understanding. We revisit this assumption by evaluating VLMs under distribution shifts, where support examples come from a dataset different from the query. Surprisingly, performance often degrades with more demonstrations, and models tend to copy answers rather than learn from them. To investigate further, we propose a new MM-ICL with Reasoning pipeline that augments each demonstration with a generated rationale alongside the answer. We conduct extensive and comprehensive experiments on both perception- and reasoning-required datasets with open-source VLMs ranging from 3B to 72B and proprietary models such as Gemini 2.0. We conduct controlled studies varying shot count, retrieval method, rationale quality, and distribution. Our results show limited performance sensitivity across these factors, suggesting that current VLMs do not effectively utilize demonstration-level information as intended in MM-ICL.
FF-PNet: A Pyramid Network Based on Feature and Field for Brain Image Registration
May 08, 2025Abstract:In recent years, deformable medical image registration techniques have made significant progress. However, existing models still lack efficiency in parallel extraction of coarse and fine-grained features. To address this, we construct a new pyramid registration network based on feature and deformation field (FF-PNet). For coarse-grained feature extraction, we design a Residual Feature Fusion Module (RFFM), for fine-grained image deformation, we propose a Residual Deformation Field Fusion Module (RDFFM). Through the parallel operation of these two modules, the model can effectively handle complex image deformations. It is worth emphasizing that the encoding stage of FF-PNet only employs traditional convolutional neural networks without any attention mechanisms or multilayer perceptrons, yet it still achieves remarkable improvements in registration accuracy, fully demonstrating the superior feature decoding capabilities of RFFM and RDFFM. We conducted extensive experiments on the LPBA and OASIS datasets. The results show our network consistently outperforms popular methods in metrics like the Dice Similarity Coefficient.
Diffusion Generative Modeling for Spatially Resolved Gene Expression Inference from Histology Images
Jan 26, 2025



Abstract:Spatial Transcriptomics (ST) allows a high-resolution measurement of RNA sequence abundance by systematically connecting cell morphology depicted in Hematoxylin and Eosin (H&E) stained histology images to spatially resolved gene expressions. ST is a time-consuming, expensive yet powerful experimental technique that provides new opportunities to understand cancer mechanisms at a fine-grained molecular level, which is critical for uncovering new approaches for disease diagnosis and treatments. Here, we present $\textbf{Stem}$ ($\textbf{S}$pa$\textbf{T}$ially resolved gene $\textbf{E}$xpression inference with diffusion $\textbf{M}$odel), a novel computational tool that leverages a conditional diffusion generative model to enable in silico gene expression inference from H&E stained images. Through better capturing the inherent stochasticity and heterogeneity in ST data, $\textbf{Stem}$ achieves state-of-the-art performance on spatial gene expression prediction and generates biologically meaningful gene profiles for new H&E stained images at test time. We evaluate the proposed algorithm on datasets with various tissue sources and sequencing platforms, where it demonstrates clear improvement over existing approaches. $\textbf{Stem}$ generates high-fidelity gene expression predictions that share similar gene variation levels as ground truth data, suggesting that our method preserves the underlying biological heterogeneity. Our proposed pipeline opens up the possibility of analyzing existing, easily accessible H&E stained histology images from a genomics point of view without physically performing gene expression profiling and empowers potential biological discovery from H&E stained histology images.
DeepSeek-V3 Technical Report
Dec 27, 2024



Abstract:We present DeepSeek-V3, a strong Mixture-of-Experts (MoE) language model with 671B total parameters with 37B activated for each token. To achieve efficient inference and cost-effective training, DeepSeek-V3 adopts Multi-head Latent Attention (MLA) and DeepSeekMoE architectures, which were thoroughly validated in DeepSeek-V2. Furthermore, DeepSeek-V3 pioneers an auxiliary-loss-free strategy for load balancing and sets a multi-token prediction training objective for stronger performance. We pre-train DeepSeek-V3 on 14.8 trillion diverse and high-quality tokens, followed by Supervised Fine-Tuning and Reinforcement Learning stages to fully harness its capabilities. Comprehensive evaluations reveal that DeepSeek-V3 outperforms other open-source models and achieves performance comparable to leading closed-source models. Despite its excellent performance, DeepSeek-V3 requires only 2.788M H800 GPU hours for its full training. In addition, its training process is remarkably stable. Throughout the entire training process, we did not experience any irrecoverable loss spikes or perform any rollbacks. The model checkpoints are available at https://github.com/deepseek-ai/DeepSeek-V3.
When Can Proxies Improve the Sample Complexity of Preference Learning?
Dec 21, 2024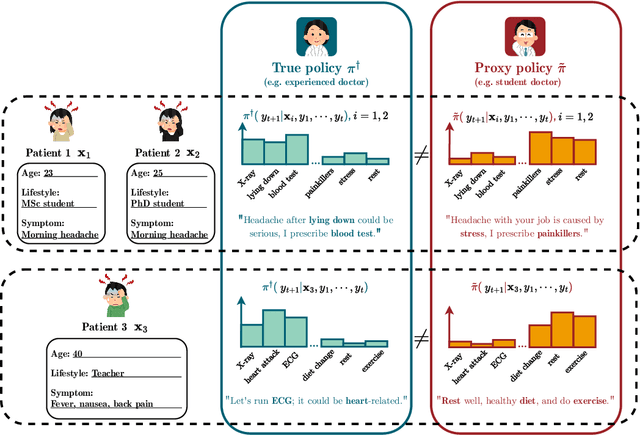
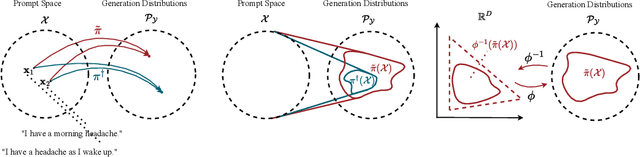
Abstract:We address the problem of reward hacking, where maximising a proxy reward does not necessarily increase the true reward. This is a key concern for Large Language Models (LLMs), as they are often fine-tuned on human preferences that may not accurately reflect a true objective. Existing work uses various tricks such as regularisation, tweaks to the reward model, and reward hacking detectors, to limit the influence that such proxy preferences have on a model. Luckily, in many contexts such as medicine, education, and law, a sparse amount of expert data is often available. In these cases, it is often unclear whether the addition of proxy data can improve policy learning. We outline a set of sufficient conditions on proxy feedback that, if satisfied, indicate that proxy data can provably improve the sample complexity of learning the ground truth policy. These conditions can inform the data collection process for specific tasks. The result implies a parameterisation for LLMs that achieves this improved sample complexity. We detail how one can adapt existing architectures to yield this improved sample complexity.
Generative modeling assisted simulation of measurement-altered quantum criticality
Dec 02, 2024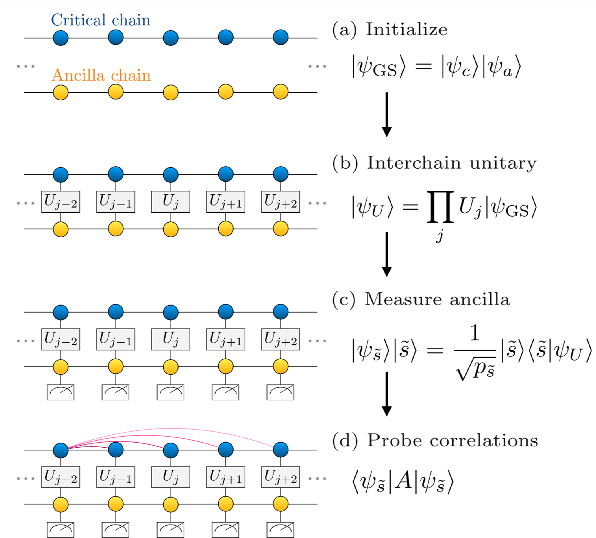
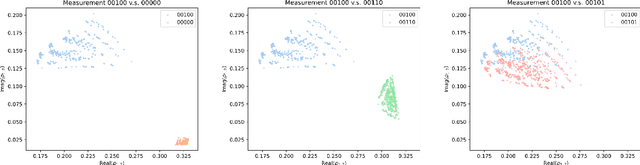
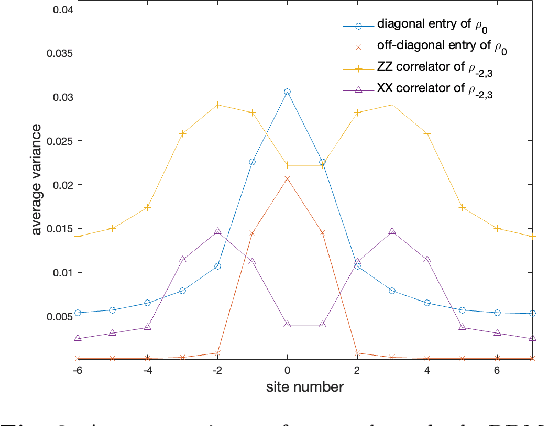
Abstract:In quantum many-body systems, measurements can induce qualitative new features, but their simulation is hindered by the exponential complexity involved in sampling the measurement results. We propose to use machine learning to assist the simulation of measurement-induced quantum phenomena. In particular, we focus on the measurement-altered quantum criticality protocol and generate local reduced density matrices of the critical chain given random measurement results. Such generation is enabled by a physics-preserving conditional diffusion generative model, which learns an observation-indexed probability distribution of an ensemble of quantum states, and then samples from that distribution given an observation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge