Deep Learning for the Multiple Optimal Stopping Problem

This paper presents a novel deep learning framework for solving multiple optimal stopping problems in high dimensions. While deep learning has recently shown promise for single stopping problems, the multiple exercise case involves complex recursive dependencies that remain challenging. We address this by combining the Dynamic Programming Principle with neural network approximation of the value function. Unlike policy-search methods, our algorithm explicitly learns the value surface. We first consider the discrete-time problem and analyze neural network training error. We then turn to continuous problems and analyze the additional error due to the discretization of the underlying stochastic processes. Numerical experiments on high-dimensional American basket options and nonlinear utility maximization demonstrate that our method provides an efficient and scalable method for the multiple optimal stopping problem.

Convergence of Actor-Critic Learning for Mean Field Games and Mean Field Control in Continuous Spaces

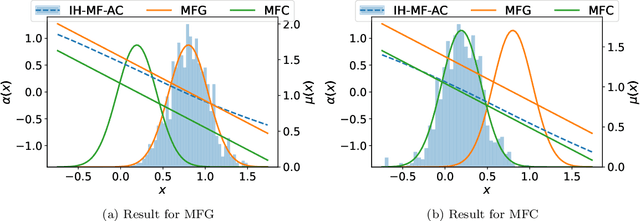
We establish the convergence of the deep actor-critic reinforcement learning algorithm presented in [Angiuli et al., 2023a] in the setting of continuous state and action spaces with an infinite discrete-time horizon. This algorithm provides solutions to Mean Field Game (MFG) or Mean Field Control (MFC) problems depending on the ratio between two learning rates: one for the value function and the other for the mean field term. In the MFC case, to rigorously identify the limit, we introduce a discretization of the state and action spaces, following the approach used in the finite-space case in [Angiuli et al., 2023b]. The convergence proofs rely on a generalization of the two-timescale framework introduced in [Borkar, 1997]. We further extend our convergence results to Mean Field Control Games, which involve locally cooperative and globally competitive populations. Finally, we present numerical experiments for linear-quadratic problems in one and two dimensions, for which explicit solutions are available.

Finite-Sample Convergence Bounds for Trust Region Policy Optimization in Mean-Field Games

We introduce Mean-Field Trust Region Policy Optimization (MF-TRPO), a novel algorithm designed to compute approximate Nash equilibria for ergodic Mean-Field Games (MFG) in finite state-action spaces. Building on the well-established performance of TRPO in the reinforcement learning (RL) setting, we extend its methodology to the MFG framework, leveraging its stability and robustness in policy optimization. Under standard assumptions in the MFG literature, we provide a rigorous analysis of MF-TRPO, establishing theoretical guarantees on its convergence. Our results cover both the exact formulation of the algorithm and its sample-based counterpart, where we derive high-probability guarantees and finite sample complexity. This work advances MFG optimization by bridging RL techniques with mean-field decision-making, offering a theoretically grounded approach to solving complex multi-agent problems.

Deep Learning Algorithms for Mean Field Optimal Stopping in Finite Space and Discrete Time

Optimal stopping is a fundamental problem in optimization that has found applications in risk management, finance, economics, and recently in the fields of computer science. We extend the standard framework to a multi-agent setting, named multi-agent optimal stopping (MAOS), where a group of agents cooperatively solves finite-space, discrete-time optimal stopping problems. Solving the finite-agent case is computationally prohibitive when the number of agents is very large, so this work studies the mean field optimal stopping (MFOS) problem, obtained as the number of agents approaches infinity. We prove that MFOS provides a good approximate solution to MAOS. We also prove a dynamic programming principle (DPP), based on the theory of mean field control. We then propose two deep learning methods: one simulates full trajectories to learn optimal decisions, whereas the other leverages DPP with backward induction; both methods train neural networks for the optimal stopping decisions. We demonstrate the effectiveness of these approaches through numerical experiments on 6 different problems in spatial dimension up to 300. To the best of our knowledge, this is the first work to study MFOS in finite space and discrete time, and to propose efficient and scalable computational methods for this type of problem.

Reinforcement Learning for Finite Space Mean-Field Type Games

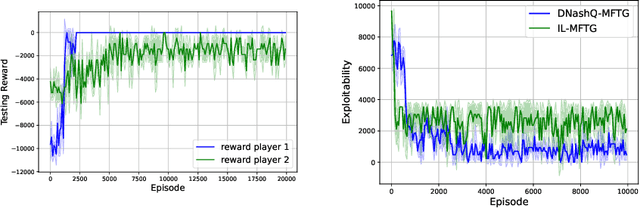
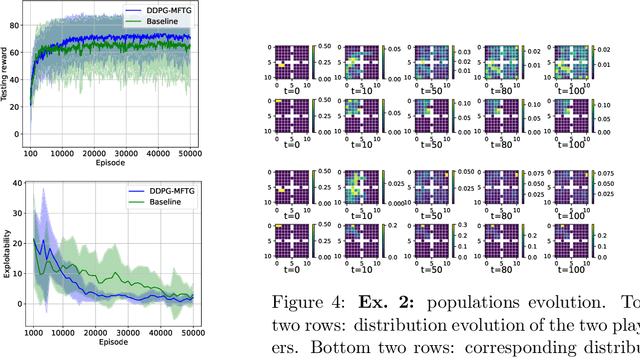
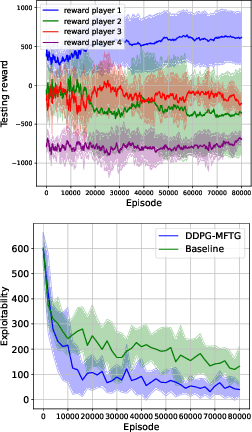
Mean field type games (MFTGs) describe Nash equilibria between large coalitions: each coalition consists of a continuum of cooperative agents who maximize the average reward of their coalition while interacting non-cooperatively with a finite number of other coalitions. Although the theory has been extensively developed, we are still lacking efficient and scalable computational methods. Here, we develop reinforcement learning methods for such games in a finite space setting with general dynamics and reward functions. We start by proving that MFTG solution yields approximate Nash equilibria in finite-size coalition games. We then propose two algorithms. The first is based on quantization of the mean-field spaces and Nash Q-learning. We provide convergence and stability analysis. We then propose an deep reinforcement learning algorithm, which can scale to larger spaces. Numerical examples on 5 environments show the scalability and the efficiency of the proposed method.

Global Solutions to Master Equations for Continuous Time Heterogeneous Agent Macroeconomic Models

We propose and compare new global solution algorithms for continuous time heterogeneous agent economies with aggregate shocks. First, we approximate the agent distribution so that equilibrium in the economy can be characterized by a high, but finite, dimensional non-linear partial differential equation. We consider different approximations: discretizing the number of agents, discretizing the agent state variables, and projecting the distribution onto a finite set of basis functions. Second, we represent the value function using a neural network and train it to solve the differential equation using deep learning tools. We refer to the solution as an Economic Model Informed Neural Network (EMINN). The main advantage of this technique is that it allows us to find global solutions to high dimensional, non-linear problems. We demonstrate our algorithm by solving important models in the macroeconomics and spatial literatures (e.g. Krusell and Smith (1998), Khan and Thomas (2007), Bilal (2023)).

Analysis of Multiscale Reinforcement Q-Learning Algorithms for Mean Field Control Games

Mean Field Control Games (MFCG), introduced in [Angiuli et al., 2022a], represent competitive games between a large number of large collaborative groups of agents in the infinite limit of number and size of groups. In this paper, we prove the convergence of a three-timescale Reinforcement Q-Learning (RL) algorithm to solve MFCG in a model-free approach from the point of view of representative agents. Our analysis uses a Q-table for finite state and action spaces updated at each discrete time-step over an infinite horizon. In [Angiuli et al., 2023], we proved convergence of two-timescale algorithms for MFG and MFC separately highlighting the need to follow multiple population distributions in the MFC case. Here, we integrate this feature for MFCG as well as three rates of update decreasing to zero in the proper ratios. Our technique of proof uses a generalization to three timescales of the two-timescale analysis in [Borkar, 1997]. We give a simple example satisfying the various hypothesis made in the proof of convergence and illustrating the performance of the algorithm.

Independent RL for Cooperative-Competitive Agents: A Mean-Field Perspective

We address in this paper Reinforcement Learning (RL) among agents that are grouped into teams such that there is cooperation within each team but general-sum (non-zero sum) competition across different teams. To develop an RL method that provably achieves a Nash equilibrium, we focus on a linear-quadratic structure. Moreover, to tackle the non-stationarity induced by multi-agent interactions in the finite population setting, we consider the case where the number of agents within each team is infinite, i.e., the mean-field setting. This results in a General-Sum LQ Mean-Field Type Game (GS-MFTGs). We characterize the Nash equilibrium (NE) of the GS-MFTG, under a standard invertibility condition. This MFTG NE is then shown to be $\mathcal{O}(1/M)$-NE for the finite population game where $M$ is a lower bound on the number of agents in each team. These structural results motivate an algorithm called Multi-player Receding-horizon Natural Policy Gradient (MRPG), where each team minimizes its cumulative cost independently in a receding-horizon manner. Despite the non-convexity of the problem, we establish that the resulting algorithm converges to a global NE through a novel problem decomposition into sub-problems using backward recursive discrete-time Hamilton-Jacobi-Isaacs (HJI) equations, in which independent natural policy gradient is shown to exhibit linear convergence under time-independent diagonal dominance. Experiments illuminate the merits of this approach in practice.

Deep Backward and Galerkin Methods for the Finite State Master Equation

This paper proposes and analyzes two neural network methods to solve the master equation for finite-state mean field games (MFGs). Solving MFGs provides approximate Nash equilibria for stochastic, differential games with finite but large populations of agents. The master equation is a partial differential equation (PDE) whose solution characterizes MFG equilibria for any possible initial distribution. The first method we propose relies on backward induction in a time component while the second method directly tackles the PDE without discretizing time. For both approaches, we prove two types of results: there exist neural networks that make the algorithms' loss functions arbitrarily small, and conversely, if the losses are small, then the neural networks are good approximations of the master equation's solution. We conclude the paper with numerical experiments on benchmark problems from the literature up to dimension 15, and a comparison with solutions computed by a classical method for fixed initial distributions.

A Deep Learning Method for Optimal Investment Under Relative Performance Criteria Among Heterogeneous Agents

Graphon games have been introduced to study games with many players who interact through a weighted graph of interaction. By passing to the limit, a game with a continuum of players is obtained, in which the interactions are through a graphon. In this paper, we focus on a graphon game for optimal investment under relative performance criteria, and we propose a deep learning method. The method builds upon two key ingredients: first, a characterization of Nash equilibria by forward-backward stochastic differential equations and, second, recent advances of machine learning algorithms for stochastic differential games. We provide numerical experiments on two different financial models. In each model, we compare the effect of several graphons, which correspond to different structures of interactions.