SENSEI: Semantic Exploration Guided by Foundation Models to Learn Versatile World Models

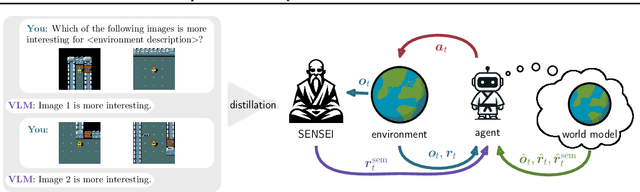
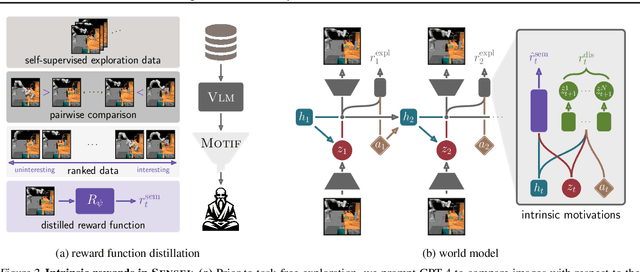
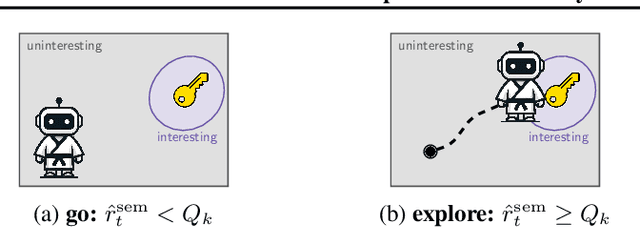
Exploration is a cornerstone of reinforcement learning (RL). Intrinsic motivation attempts to decouple exploration from external, task-based rewards. However, established approaches to intrinsic motivation that follow general principles such as information gain, often only uncover low-level interactions. In contrast, children's play suggests that they engage in meaningful high-level behavior by imitating or interacting with their caregivers. Recent work has focused on using foundation models to inject these semantic biases into exploration. However, these methods often rely on unrealistic assumptions, such as language-embedded environments or access to high-level actions. We propose SEmaNtically Sensible ExploratIon (SENSEI), a framework to equip model-based RL agents with an intrinsic motivation for semantically meaningful behavior. SENSEI distills a reward signal of interestingness from Vision Language Model (VLM) annotations, enabling an agent to predict these rewards through a world model. Using model-based RL, SENSEI trains an exploration policy that jointly maximizes semantic rewards and uncertainty. We show that in both robotic and video game-like simulations SENSEI discovers a variety of meaningful behaviors from image observations and low-level actions. SENSEI provides a general tool for learning from foundation model feedback, a crucial research direction, as VLMs become more powerful.

Dual-Force: Enhanced Offline Diversity Maximization under Imitation Constraints

While many algorithms for diversity maximization under imitation constraints are online in nature, many applications require offline algorithms without environment interactions. Tackling this problem in the offline setting, however, presents significant challenges that require non-trivial, multi-stage optimization processes with non-stationary rewards. In this work, we present a novel offline algorithm that enhances diversity using an objective based on Van der Waals (VdW) force and successor features, and eliminates the need to learn a previously used skill discriminator. Moreover, by conditioning the value function and policy on a pre-trained Functional Reward Encoding (FRE), our method allows for better handling of non-stationary rewards and provides zero-shot recall of all skills encountered during training, significantly expanding the set of skills learned in prior work. Consequently, our algorithm benefits from receiving a consistently strong diversity signal (VdW), and enjoys more stable and efficient training. We demonstrate the effectiveness of our method in generating diverse skills for two robotic tasks in simulation: locomotion of a quadruped and local navigation with obstacle traversal.

Learning Diverse Skills for Local Navigation under Multi-constraint Optimality

Despite many successful applications of data-driven control in robotics, extracting meaningful diverse behaviors remains a challenge. Typically, task performance needs to be compromised in order to achieve diversity. In many scenarios, task requirements are specified as a multitude of reward terms, each requiring a different trade-off. In this work, we take a constrained optimization viewpoint on the quality-diversity trade-off and show that we can obtain diverse policies while imposing constraints on their value functions which are defined through distinct rewards. In line with previous work, further control of the diversity level can be achieved through an attract-repel reward term motivated by the Van der Waals force. We demonstrate the effectiveness of our method on a local navigation task where a quadruped robot needs to reach the target within a finite horizon. Finally, our trained policies transfer well to the real 12-DoF quadruped robot, Solo12, and exhibit diverse agile behaviors with successful obstacle traversal.

Real Robot Challenge 2022: Learning Dexterous Manipulation from Offline Data in the Real World

Experimentation on real robots is demanding in terms of time and costs. For this reason, a large part of the reinforcement learning (RL) community uses simulators to develop and benchmark algorithms. However, insights gained in simulation do not necessarily translate to real robots, in particular for tasks involving complex interactions with the environment. The Real Robot Challenge 2022 therefore served as a bridge between the RL and robotics communities by allowing participants to experiment remotely with a real robot - as easily as in simulation. In the last years, offline reinforcement learning has matured into a promising paradigm for learning from pre-collected datasets, alleviating the reliance on expensive online interactions. We therefore asked the participants to learn two dexterous manipulation tasks involving pushing, grasping, and in-hand orientation from provided real-robot datasets. An extensive software documentation and an initial stage based on a simulation of the real set-up made the competition particularly accessible. By giving each team plenty of access budget to evaluate their offline-learned policies on a cluster of seven identical real TriFinger platforms, we organized an exciting competition for machine learners and roboticists alike. In this work we state the rules of the competition, present the methods used by the winning teams and compare their results with a benchmark of state-of-the-art offline RL algorithms on the challenge datasets.

Benchmarking Offline Reinforcement Learning on Real-Robot Hardware

Learning policies from previously recorded data is a promising direction for real-world robotics tasks, as online learning is often infeasible. Dexterous manipulation in particular remains an open problem in its general form. The combination of offline reinforcement learning with large diverse datasets, however, has the potential to lead to a breakthrough in this challenging domain analogously to the rapid progress made in supervised learning in recent years. To coordinate the efforts of the research community toward tackling this problem, we propose a benchmark including: i) a large collection of data for offline learning from a dexterous manipulation platform on two tasks, obtained with capable RL agents trained in simulation; ii) the option to execute learned policies on a real-world robotic system and a simulation for efficient debugging. We evaluate prominent open-sourced offline reinforcement learning algorithms on the datasets and provide a reproducible experimental setup for offline reinforcement learning on real systems.

Diverse Offline Imitation via Fenchel Duality

There has been significant recent progress in the area of unsupervised skill discovery, with various works proposing mutual information based objectives, as a source of intrinsic motivation. Prior works predominantly focused on designing algorithms that require online access to the environment. In contrast, we develop an \textit{offline} skill discovery algorithm. Our problem formulation considers the maximization of a mutual information objective constrained by a KL-divergence. More precisely, the constraints ensure that the state occupancy of each skill remains close to the state occupancy of an expert, within the support of an offline dataset with good state-action coverage. Our main contribution is to connect Fenchel duality, reinforcement learning and unsupervised skill discovery, and to give a simple offline algorithm for learning diverse skills that are aligned with an expert.

On Imitation in Mean-field Games

We explore the problem of imitation learning (IL) in the context of mean-field games (MFGs), where the goal is to imitate the behavior of a population of agents following a Nash equilibrium policy according to some unknown payoff function. IL in MFGs presents new challenges compared to single-agent IL, particularly when both the reward function and the transition kernel depend on the population distribution. In this paper, departing from the existing literature on IL for MFGs, we introduce a new solution concept called the Nash imitation gap. Then we show that when only the reward depends on the population distribution, IL in MFGs can be reduced to single-agent IL with similar guarantees. However, when the dynamics is population-dependent, we provide a novel upper-bound that suggests IL is harder in this setting. To address this issue, we propose a new adversarial formulation where the reinforcement learning problem is replaced by a mean-field control (MFC) problem, suggesting progress in IL within MFGs may have to build upon MFC.

Online Learning under Adversarial Nonlinear Constraints

In many applications, learning systems are required to process continuous non-stationary data streams. We study this problem in an online learning framework and propose an algorithm that can deal with adversarial time-varying and nonlinear constraints. As we show in our work, the algorithm called Constraint Violation Velocity Projection (CVV-Pro) achieves $\sqrt{T}$ regret and converges to the feasible set at a rate of $1/\sqrt{T}$, despite the fact that the feasible set is slowly time-varying and a priori unknown to the learner. CVV-Pro only relies on local sparse linear approximations of the feasible set and therefore avoids optimizing over the entire set at each iteration, which is in sharp contrast to projected gradients or Frank-Wolfe methods. We also empirically evaluate our algorithm on two-player games, where the players are subjected to a shared constraint.

Versatile Skill Control via Self-supervised Adversarial Imitation of Unlabeled Mixed Motions

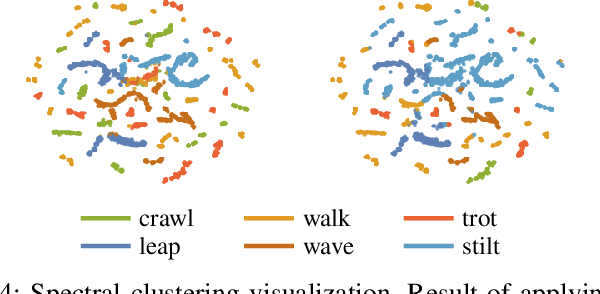
Learning diverse skills is one of the main challenges in robotics. To this end, imitation learning approaches have achieved impressive results. These methods require explicitly labeled datasets or assume consistent skill execution to enable learning and active control of individual behaviors, which limits their applicability. In this work, we propose a cooperative adversarial method for obtaining single versatile policies with controllable skill sets from unlabeled datasets containing diverse state transition patterns by maximizing their discriminability. Moreover, we show that by utilizing unsupervised skill discovery in the generative adversarial imitation learning framework, novel and useful skills emerge with successful task fulfillment. Finally, the obtained versatile policies are tested on an agile quadruped robot called Solo 8 and present faithful replications of diverse skills encoded in the demonstrations.

Physarum Multi-Commodity Flow Dynamics

In wet-lab experiments \cite{Nakagaki-Yamada-Toth,Tero-Takagi-etal}, the slime mold Physarum polycephalum has demonstrated its ability to solve shortest path problems and to design efficient networks, see Figure \ref{Wet-Lab Experiments} for illustrations. Physarum polycephalum is a slime mold in the Mycetozoa group. For the shortest path problem, a mathematical model for the evolution of the slime was proposed in \cite{Tero-Kobayashi-Nakagaki} and its biological relevance was argued. The model was shown to solve shortest path problems, first in computer simulations and then by mathematical proof. It was later shown that the slime mold dynamics can solve more general linear programs and that many variants of the dynamics have similar convergence behavior. In this paper, we introduce a dynamics for the network design problem. We formulate network design as the problem of constructing a network that efficiently supports a multi-commodity flow problem. We investigate the dynamics in computer simulations and analytically. The simulations show that the dynamics is able to construct efficient and elegant networks. In the theoretical part we show that the dynamics minimizes an objective combining the cost of the network and the cost of routing the demands through the network. We also give alternative characterization of the optimum solution.