Golnoosh Shahkarami
Learning-Augmented Algorithms for Online TSP on the Line
Jun 01, 2022



Abstract:We study the online Traveling Salesman Problem (TSP) on the line augmented with machine-learned predictions. In the classical problem, there is a stream of requests released over time along the real line. The goal is to minimize the makespan of the algorithm. We distinguish between the open variant and the closed one, in which we additionally require the algorithm to return to the origin after serving all requests. The state of the art is a $1.64$-competitive algorithm and a $2.04$-competitive algorithm for the closed and open variants, respectively \cite{Bjelde:1.64}. In both cases, a tight lower bound is known \cite{Ausiello:1.75, Bjelde:1.64}. In both variants, our primary prediction model involves predicted positions of the requests. We introduce algorithms that (i) obtain a tight 1.5 competitive ratio for the closed variant and a 1.66 competitive ratio for the open variant in the case of perfect predictions, (ii) are robust against unbounded prediction error, and (iii) are smooth, i.e., their performance degrades gracefully as the prediction error increases. Moreover, we further investigate the learning-augmented setting in the open variant by additionally considering a prediction for the last request served by the optimal offline algorithm. Our algorithm for this enhanced setting obtains a 1.33 competitive ratio with perfect predictions while also being smooth and robust, beating the lower bound of 1.44 we show for our original prediction setting for the open variant. Also, we provide a lower bound of 1.25 for this enhanced setting.
A Novel Prediction Setup for Online Speed-Scaling
Dec 06, 2021



Abstract:Given the rapid rise in energy demand by data centers and computing systems in general, it is fundamental to incorporate energy considerations when designing (scheduling) algorithms. Machine learning can be a useful approach in practice by predicting the future load of the system based on, for example, historical data. However, the effectiveness of such an approach highly depends on the quality of the predictions and can be quite far from optimal when predictions are sub-par. On the other hand, while providing a worst-case guarantee, classical online algorithms can be pessimistic for large classes of inputs arising in practice. This paper, in the spirit of the new area of machine learning augmented algorithms, attempts to obtain the best of both worlds for the classical, deadline based, online speed-scaling problem: Based on the introduction of a novel prediction setup, we develop algorithms that (i) obtain provably low energy-consumption in the presence of adequate predictions, and (ii) are robust against inadequate predictions, and (iii) are smooth, i.e., their performance gradually degrades as the prediction error increases.
Physarum Multi-Commodity Flow Dynamics
Sep 23, 2020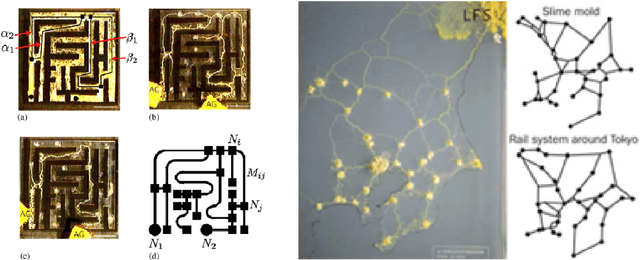
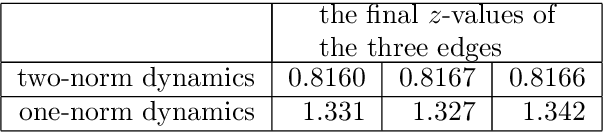
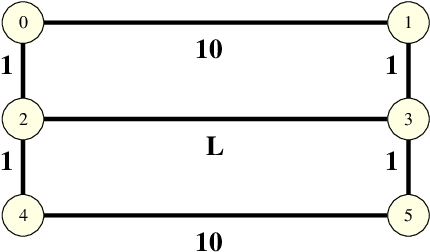
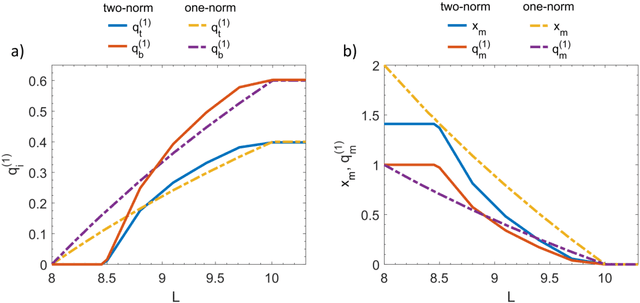
Abstract:In wet-lab experiments \cite{Nakagaki-Yamada-Toth,Tero-Takagi-etal}, the slime mold Physarum polycephalum has demonstrated its ability to solve shortest path problems and to design efficient networks, see Figure \ref{Wet-Lab Experiments} for illustrations. Physarum polycephalum is a slime mold in the Mycetozoa group. For the shortest path problem, a mathematical model for the evolution of the slime was proposed in \cite{Tero-Kobayashi-Nakagaki} and its biological relevance was argued. The model was shown to solve shortest path problems, first in computer simulations and then by mathematical proof. It was later shown that the slime mold dynamics can solve more general linear programs and that many variants of the dynamics have similar convergence behavior. In this paper, we introduce a dynamics for the network design problem. We formulate network design as the problem of constructing a network that efficiently supports a multi-commodity flow problem. We investigate the dynamics in computer simulations and analytically. The simulations show that the dynamics is able to construct efficient and elegant networks. In the theoretical part we show that the dynamics minimizes an objective combining the cost of the network and the cost of routing the demands through the network. We also give alternative characterization of the optimum solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge