Andreas Karrenbauer
Physarum Multi-Commodity Flow Dynamics
Sep 23, 2020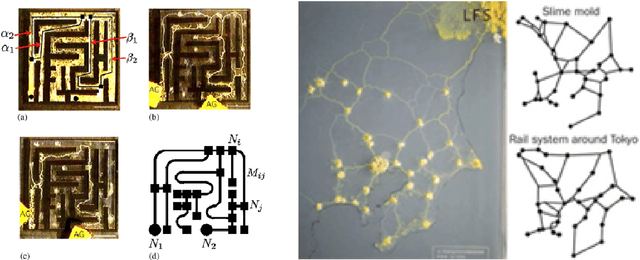
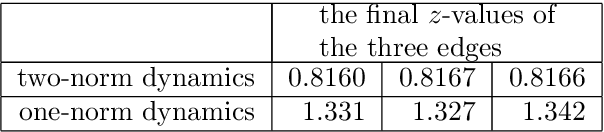
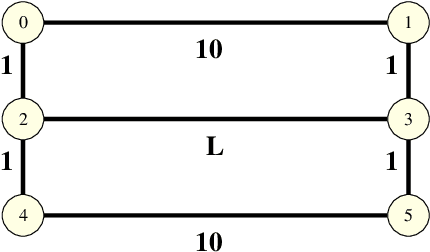
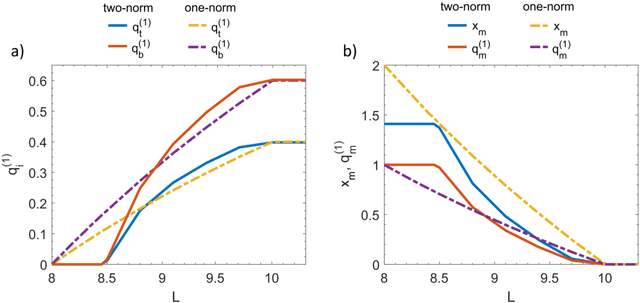
Abstract:In wet-lab experiments \cite{Nakagaki-Yamada-Toth,Tero-Takagi-etal}, the slime mold Physarum polycephalum has demonstrated its ability to solve shortest path problems and to design efficient networks, see Figure \ref{Wet-Lab Experiments} for illustrations. Physarum polycephalum is a slime mold in the Mycetozoa group. For the shortest path problem, a mathematical model for the evolution of the slime was proposed in \cite{Tero-Kobayashi-Nakagaki} and its biological relevance was argued. The model was shown to solve shortest path problems, first in computer simulations and then by mathematical proof. It was later shown that the slime mold dynamics can solve more general linear programs and that many variants of the dynamics have similar convergence behavior. In this paper, we introduce a dynamics for the network design problem. We formulate network design as the problem of constructing a network that efficiently supports a multi-commodity flow problem. We investigate the dynamics in computer simulations and analytically. The simulations show that the dynamics is able to construct efficient and elegant networks. In the theoretical part we show that the dynamics minimizes an objective combining the cost of the network and the cost of routing the demands through the network. We also give alternative characterization of the optimum solution.
Blinking Molecule Tracking
Mar 29, 2013

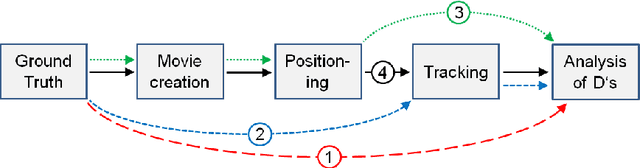
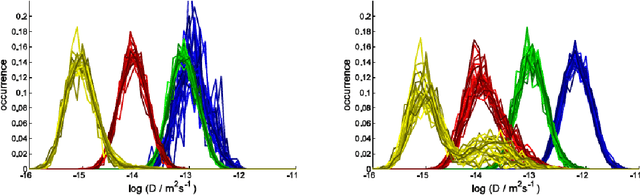
Abstract:We discuss a method for tracking individual molecules which globally optimizes the likelihood of the connections between molecule positions fast and with high reliability even for high spot densities and blinking molecules. Our method works with cost functions which can be freely chosen to combine costs for distances between spots in space and time and which can account for the reliability of positioning a molecule. To this end, we describe a top-down polyhedral approach to the problem of tracking many individual molecules. This immediately yields an effective implementation using standard linear programming solvers. Our method can be applied to 2D and 3D tracking.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge