Product distribution learning with imperfect advice

Given i.i.d.~samples from an unknown distribution $P$, the goal of distribution learning is to recover the parameters of a distribution that is close to $P$. When $P$ belongs to the class of product distributions on the Boolean hypercube $\{0,1\}^d$, it is known that $Ω(d/\varepsilon^2)$ samples are necessary to learn $P$ within total variation (TV) distance $\varepsilon$. We revisit this problem when the learner is also given as advice the parameters of a product distribution $Q$. We show that there is an efficient algorithm to learn $P$ within TV distance $\varepsilon$ that has sample complexity $\tilde{O}(d^{1-η}/\varepsilon^2)$, if $\|\mathbf{p} - \mathbf{q}\|_1 < \varepsilon d^{0.5 - Ω(η)}$. Here, $\mathbf{p}$ and $\mathbf{q}$ are the mean vectors of $P$ and $Q$ respectively, and no bound on $\|\mathbf{p} - \mathbf{q}\|_1$ is known to the algorithm a priori.

Learning High-dimensional Gaussians from Censored Data

We provide efficient algorithms for the problem of distribution learning from high-dimensional Gaussian data where in each sample, some of the variable values are missing. We suppose that the variables are missing not at random (MNAR). The missingness model, denoted by $S(y)$, is the function that maps any point $y$ in $R^d$ to the subsets of its coordinates that are seen. In this work, we assume that it is known. We study the following two settings: (i) Self-censoring: An observation $x$ is generated by first sampling the true value $y$ from a $d$-dimensional Gaussian $N(\mu*, \Sigma*)$ with unknown $\mu*$ and $\Sigma*$. For each coordinate $i$, there exists a set $S_i$ subseteq $R^d$ such that $x_i = y_i$ if and only if $y_i$ in $S_i$. Otherwise, $x_i$ is missing and takes a generic value (e.g., "?"). We design an algorithm that learns $N(\mu*, \Sigma*)$ up to total variation (TV) distance epsilon, using $poly(d, 1/\epsilon)$ samples, assuming only that each pair of coordinates is observed with sufficiently high probability. (ii) Linear thresholding: An observation $x$ is generated by first sampling $y$ from a $d$-dimensional Gaussian $N(\mu*, \Sigma)$ with unknown $\mu*$ and known $\Sigma$, and then applying the missingness model $S$ where $S(y) = {i in [d] : v_i^T y <= b_i}$ for some $v_1, ..., v_d$ in $R^d$ and $b_1, ..., b_d$ in $R$. We design an efficient mean estimation algorithm, assuming that none of the possible missingness patterns is very rare conditioned on the values of the observed coordinates and that any small subset of coordinates is observed with sufficiently high probability.

Learning multivariate Gaussians with imperfect advice

We revisit the problem of distribution learning within the framework of learning-augmented algorithms. In this setting, we explore the scenario where a probability distribution is provided as potentially inaccurate advice on the true, unknown distribution. Our objective is to develop learning algorithms whose sample complexity decreases as the quality of the advice improves, thereby surpassing standard learning lower bounds when the advice is sufficiently accurate. Specifically, we demonstrate that this outcome is achievable for the problem of learning a multivariate Gaussian distribution $N(\boldsymbol{\mu}, \boldsymbol{\Sigma})$ in the PAC learning setting. Classically, in the advice-free setting, $\tilde{\Theta}(d^2/\varepsilon^2)$ samples are sufficient and worst case necessary to learn $d$-dimensional Gaussians up to TV distance $\varepsilon$ with constant probability. When we are additionally given a parameter $\tilde{\boldsymbol{\Sigma}}$ as advice, we show that $\tilde{O}(d^{2-\beta}/\varepsilon^2)$ samples suffices whenever $\| \tilde{\boldsymbol{\Sigma}}^{-1/2} \boldsymbol{\Sigma} \tilde{\boldsymbol{\Sigma}}^{-1/2} - \boldsymbol{I_d} \|_1 \leq \varepsilon d^{1-\beta}$ (where $\|\cdot\|_1$ denotes the entrywise $\ell_1$ norm) for any $\beta > 0$, yielding a polynomial improvement over the advice-free setting.

Online bipartite matching with imperfect advice

We study the problem of online unweighted bipartite matching with $n$ offline vertices and $n$ online vertices where one wishes to be competitive against the optimal offline algorithm. While the classic RANKING algorithm of Karp et al. [1990] provably attains competitive ratio of $1-1/e > 1/2$, we show that no learning-augmented method can be both 1-consistent and strictly better than $1/2$-robust under the adversarial arrival model. Meanwhile, under the random arrival model, we show how one can utilize methods from distribution testing to design an algorithm that takes in external advice about the online vertices and provably achieves competitive ratio interpolating between any ratio attainable by advice-free methods and the optimal ratio of 1, depending on the advice quality.

Active causal structure learning with advice

We introduce the problem of active causal structure learning with advice. In the typical well-studied setting, the learning algorithm is given the essential graph for the observational distribution and is asked to recover the underlying causal directed acyclic graph (DAG) $G^*$ while minimizing the number of interventions made. In our setting, we are additionally given side information about $G^*$ as advice, e.g. a DAG $G$ purported to be $G^*$. We ask whether the learning algorithm can benefit from the advice when it is close to being correct, while still having worst-case guarantees even when the advice is arbitrarily bad. Our work is in the same space as the growing body of research on algorithms with predictions. When the advice is a DAG $G$, we design an adaptive search algorithm to recover $G^*$ whose intervention cost is at most $O(\max\{1, \log \psi\})$ times the cost for verifying $G^*$; here, $\psi$ is a distance measure between $G$ and $G^*$ that is upper bounded by the number of variables $n$, and is exactly 0 when $G=G^*$. Our approximation factor matches the state-of-the-art for the advice-less setting.

Learning-Augmented Algorithms for Online TSP on the Line

We study the online Traveling Salesman Problem (TSP) on the line augmented with machine-learned predictions. In the classical problem, there is a stream of requests released over time along the real line. The goal is to minimize the makespan of the algorithm. We distinguish between the open variant and the closed one, in which we additionally require the algorithm to return to the origin after serving all requests. The state of the art is a $1.64$-competitive algorithm and a $2.04$-competitive algorithm for the closed and open variants, respectively \cite{Bjelde:1.64}. In both cases, a tight lower bound is known \cite{Ausiello:1.75, Bjelde:1.64}. In both variants, our primary prediction model involves predicted positions of the requests. We introduce algorithms that (i) obtain a tight 1.5 competitive ratio for the closed variant and a 1.66 competitive ratio for the open variant in the case of perfect predictions, (ii) are robust against unbounded prediction error, and (iii) are smooth, i.e., their performance degrades gracefully as the prediction error increases. Moreover, we further investigate the learning-augmented setting in the open variant by additionally considering a prediction for the last request served by the optimal offline algorithm. Our algorithm for this enhanced setting obtains a 1.33 competitive ratio with perfect predictions while also being smooth and robust, beating the lower bound of 1.44 we show for our original prediction setting for the open variant. Also, we provide a lower bound of 1.25 for this enhanced setting.

Learning Augmented Online Facility Location

Following the research agenda initiated by Munoz & Vassilvitskii [1] and Lykouris & Vassilvitskii [2] on learning-augmented online algorithms for classical online optimization problems, in this work, we consider the Online Facility Location problem under this framework. In Online Facility Location (OFL), demands arrive one-by-one in a metric space and must be (irrevocably) assigned to an open facility upon arrival, without any knowledge about future demands. We present an online algorithm for OFL that exploits potentially imperfect predictions on the locations of the optimal facilities. We prove that the competitive ratio decreases smoothly from sublogarithmic in the number of demands to constant, as the error, i.e., the total distance of the predicted locations to the optimal facility locations, decreases towards zero. We complement our analysis with a matching lower bound establishing that the dependence of the algorithm's competitive ratio on the error is optimal, up to constant factors. Finally, we evaluate our algorithm on real world data and compare our learning augmented approach with the current best online algorithm for the problem.

Computationally and Statistically Efficient Truncated Regression

We provide a computationally and statistically efficient estimator for the classical problem of truncated linear regression, where the dependent variable $y = w^T x + \epsilon$ and its corresponding vector of covariates $x \in R^k$ are only revealed if the dependent variable falls in some subset $S \subseteq R$; otherwise the existence of the pair $(x, y)$ is hidden. This problem has remained a challenge since the early works of [Tobin 1958, Amemiya 1973, Hausman and Wise 1977], its applications are abundant, and its history dates back even further to the work of Galton, Pearson, Lee, and Fisher. While consistent estimators of the regression coefficients have been identified, the error rates are not well-understood, especially in high dimensions. Under a thickness assumption about the covariance matrix of the covariates in the revealed sample, we provide a computationally efficient estimator for the coefficient vector $w$ from $n$ revealed samples that attains $l_2$ error $\tilde{O}(\sqrt{k/n})$. Our estimator uses Projected Stochastic Gradient Descent (PSGD) without replacement on the negative log-likelihood of the truncated sample. For the statistically efficient estimation we only need oracle access to the set $S$.In order to achieve computational efficiency we need to assume that $S$ is a union of a finite number of intervals but still can be complicated. PSGD without replacement must be restricted to an appropriately defined convex cone to guarantee that the negative log-likelihood is strongly convex, which in turn is established using concentration of matrices on variables with sub-exponential tails. We perform experiments on simulated data to illustrate the accuracy of our estimator. As a corollary, we show that SGD learns the parameters of single-layer neural networks with noisy activation functions.

Robust Learning under Strong Noise via SQs

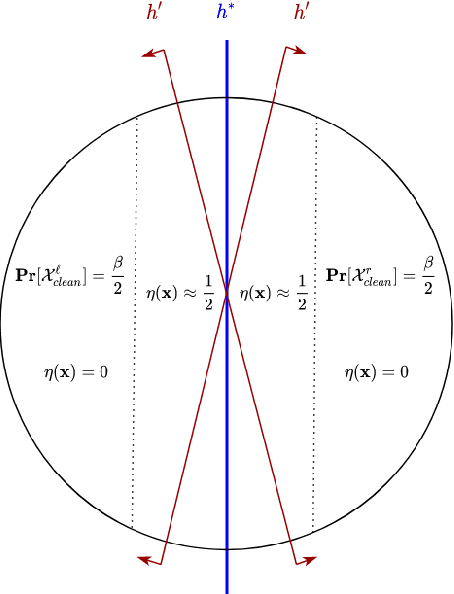
This work provides several new insights on the robustness of Kearns' statistical query framework against challenging label-noise models. First, we build on a recent result by \cite{DBLP:journals/corr/abs-2006-04787} that showed noise tolerance of distribution-independently evolvable concept classes under Massart noise. Specifically, we extend their characterization to more general noise models, including the Tsybakov model which considerably generalizes the Massart condition by allowing the flipping probability to be arbitrarily close to $\frac{1}{2}$ for a subset of the domain. As a corollary, we employ an evolutionary algorithm by \cite{DBLP:conf/colt/KanadeVV10} to obtain the first polynomial time algorithm with arbitrarily small excess error for learning linear threshold functions over any spherically symmetric distribution in the presence of spherically symmetric Tsybakov noise. Moreover, we posit access to a stronger oracle, in which for every labeled example we additionally obtain its flipping probability. In this model, we show that every SQ learnable class admits an efficient learning algorithm with OPT + $\epsilon$ misclassification error for a broad class of noise models. This setting substantially generalizes the widely-studied problem of classification under RCN with known noise rate, and corresponds to a non-convex optimization problem even when the noise function -- i.e. the flipping probabilities of all points -- is known in advance.

Optimal Testing of Discrete Distributions with High Probability

We study the problem of testing discrete distributions with a focus on the high probability regime. Specifically, given samples from one or more discrete distributions, a property $\mathcal{P}$, and parameters $0< \epsilon, \delta <1$, we want to distinguish {\em with probability at least $1-\delta$} whether these distributions satisfy $\mathcal{P}$ or are $\epsilon$-far from $\mathcal{P}$ in total variation distance. Most prior work in distribution testing studied the constant confidence case (corresponding to $\delta = \Omega(1)$), and provided sample-optimal testers for a range of properties. While one can always boost the confidence probability of any such tester by black-box amplification, this generic boosting method typically leads to sub-optimal sample bounds. Here we study the following broad question: For a given property $\mathcal{P}$, can we {\em characterize} the sample complexity of testing $\mathcal{P}$ as a function of all relevant problem parameters, including the error probability $\delta$? Prior to this work, uniformity testing was the only statistical task whose sample complexity had been characterized in this setting. As our main results, we provide the first algorithms for closeness and independence testing that are sample-optimal, within constant factors, as a function of all relevant parameters. We also show matching information-theoretic lower bounds on the sample complexity of these problems. Our techniques naturally extend to give optimal testers for related problems. To illustrate the generality of our methods, we give optimal algorithms for testing collections of distributions and testing closeness with unequal sized samples.