Reducing Oversmoothing through Informed Weight Initialization in Graph Neural Networks

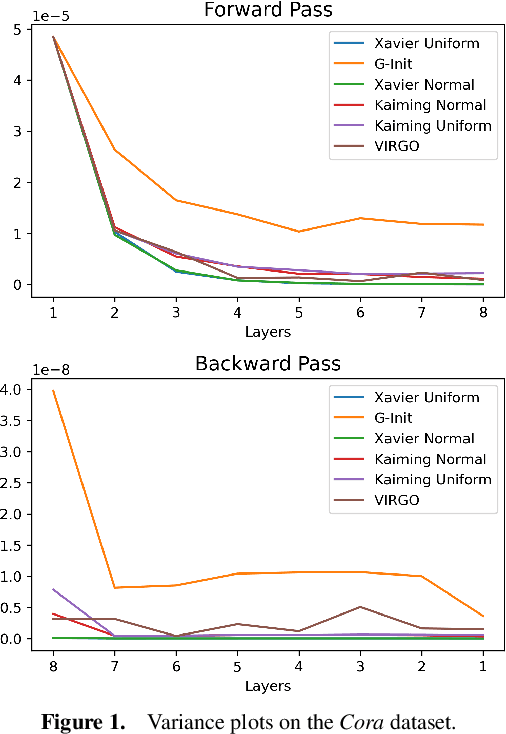
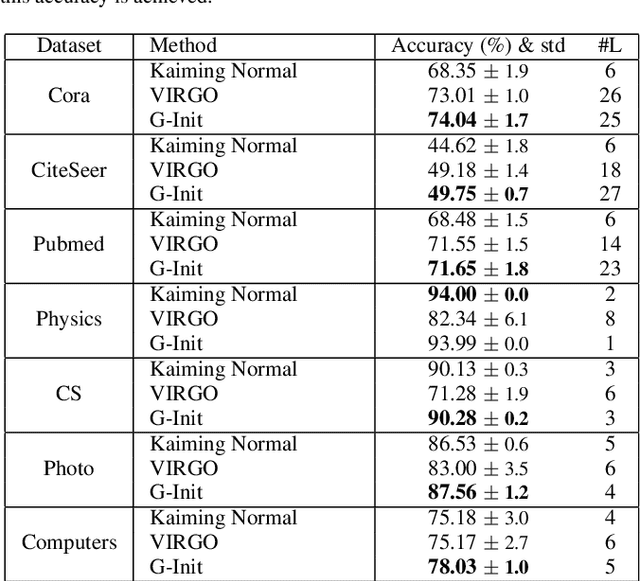
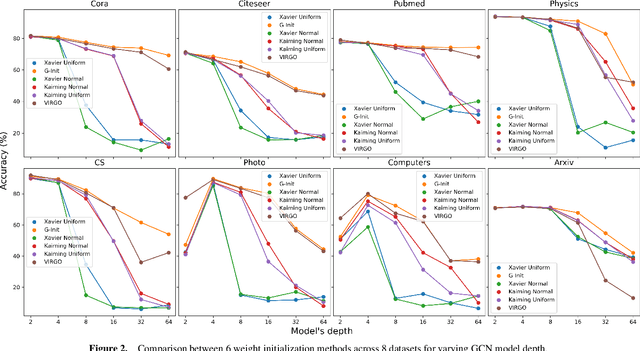
In this work, we generalize the ideas of Kaiming initialization to Graph Neural Networks (GNNs) and propose a new scheme (G-Init) that reduces oversmoothing, leading to very good results in node and graph classification tasks. GNNs are commonly initialized using methods designed for other types of Neural Networks, overlooking the underlying graph topology. We analyze theoretically the variance of signals flowing forward and gradients flowing backward in the class of convolutional GNNs. We then simplify our analysis to the case of the GCN and propose a new initialization method. Our results indicate that the new method (G-Init) reduces oversmoothing in deep GNNs, facilitating their effective use. Experimental validation supports our theoretical findings, demonstrating the advantages of deep networks in scenarios with no feature information for unlabeled nodes (i.e., ``cold start'' scenario).

Partially Trained Graph Convolutional Networks Resist Oversmoothing

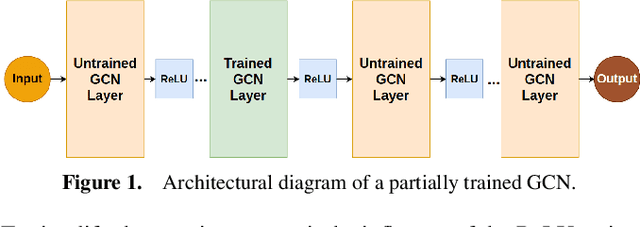
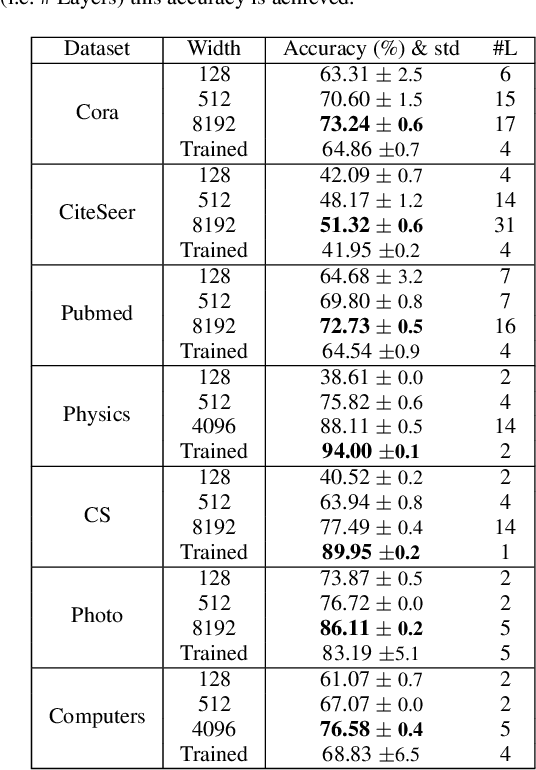
In this work we investigate an observation made by Kipf \& Welling, who suggested that untrained GCNs can generate meaningful node embeddings. In particular, we investigate the effect of training only a single layer of a GCN, while keeping the rest of the layers frozen. We propose a basis on which the effect of the untrained layers and their contribution to the generation of embeddings can be predicted. Moreover, we show that network width influences the dissimilarity of node embeddings produced after the initial node features pass through the untrained part of the model. Additionally, we establish a connection between partially trained GCNs and oversmoothing, showing that they are capable of reducing it. We verify our theoretical results experimentally and show the benefits of using deep networks that resist oversmoothing, in a ``cold start'' scenario, where there is a lack of feature information for unlabeled nodes.

GLANCE: Global Actions in a Nutshell for Counterfactual Explainability

Counterfactual explanations have emerged as an important tool to understand, debug, and audit complex machine learning models. To offer global counterfactual explainability, state-of-the-art methods construct summaries of local explanations, offering a trade-off among conciseness, counterfactual effectiveness, and counterfactual cost or burden imposed on instances. In this work, we provide a concise formulation of the problem of identifying global counterfactuals and establish principled criteria for comparing solutions, drawing inspiration from Pareto dominance. We introduce innovative algorithms designed to address the challenge of finding global counterfactuals for either the entire input space or specific partitions, employing clustering and decision trees as key components. Additionally, we conduct a comprehensive experimental evaluation, considering various instances of the problem and comparing our proposed algorithms with state-of-the-art methods. The results highlight the consistent capability of our algorithms to generate meaningful and interpretable global counterfactual explanations.

Fairness in Ranking: Robustness through Randomization without the Protected Attribute

There has been great interest in fairness in machine learning, especially in relation to classification problems. In ranking-related problems, such as in online advertising, recommender systems, and HR automation, much work on fairness remains to be done. Two complications arise: first, the protected attribute may not be available in many applications. Second, there are multiple measures of fairness of rankings, and optimization-based methods utilizing a single measure of fairness of rankings may produce rankings that are unfair with respect to other measures. In this work, we propose a randomized method for post-processing rankings, which do not require the availability of the protected attribute. In an extensive numerical study, we show the robustness of our methods with respect to P-Fairness and effectiveness with respect to Normalized Discounted Cumulative Gain (NDCG) from the baseline ranking, improving on previously proposed methods.

Optimizing Solution-Samplers for Combinatorial Problems: The Landscape of Policy-Gradient Methods

Deep Neural Networks and Reinforcement Learning methods have empirically shown great promise in tackling challenging combinatorial problems. In those methods a deep neural network is used as a solution generator which is then trained by gradient-based methods (e.g., policy gradient) to successively obtain better solution distributions. In this work we introduce a novel theoretical framework for analyzing the effectiveness of such methods. We ask whether there exist generative models that (i) are expressive enough to generate approximately optimal solutions; (ii) have a tractable, i.e, polynomial in the size of the input, number of parameters; (iii) their optimization landscape is benign in the sense that it does not contain sub-optimal stationary points. Our main contribution is a positive answer to this question. Our result holds for a broad class of combinatorial problems including Max- and Min-Cut, Max-$k$-CSP, Maximum-Weight-Bipartite-Matching, and the Traveling Salesman Problem. As a byproduct of our analysis we introduce a novel regularization process over vanilla gradient descent and provide theoretical and experimental evidence that it helps address vanishing-gradient issues and escape bad stationary points.

Fairness Aware Counterfactuals for Subgroups

In this work, we present Fairness Aware Counterfactuals for Subgroups (FACTS), a framework for auditing subgroup fairness through counterfactual explanations. We start with revisiting (and generalizing) existing notions and introducing new, more refined notions of subgroup fairness. We aim to (a) formulate different aspects of the difficulty of individuals in certain subgroups to achieve recourse, i.e. receive the desired outcome, either at the micro level, considering members of the subgroup individually, or at the macro level, considering the subgroup as a whole, and (b) introduce notions of subgroup fairness that are robust, if not totally oblivious, to the cost of achieving recourse. We accompany these notions with an efficient, model-agnostic, highly parameterizable, and explainable framework for evaluating subgroup fairness. We demonstrate the advantages, the wide applicability, and the efficiency of our approach through a thorough experimental evaluation of different benchmark datasets.

Perfect Sampling from Pairwise Comparisons

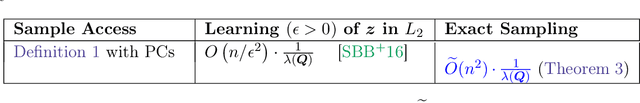
In this work, we study how to efficiently obtain perfect samples from a discrete distribution $\mathcal{D}$ given access only to pairwise comparisons of elements of its support. Specifically, we assume access to samples $(x, S)$, where $S$ is drawn from a distribution over sets $\mathcal{Q}$ (indicating the elements being compared), and $x$ is drawn from the conditional distribution $\mathcal{D}_S$ (indicating the winner of the comparison) and aim to output a clean sample $y$ distributed according to $\mathcal{D}$. We mainly focus on the case of pairwise comparisons where all sets $S$ have size 2. We design a Markov chain whose stationary distribution coincides with $\mathcal{D}$ and give an algorithm to obtain exact samples using the technique of Coupling from the Past. However, the sample complexity of this algorithm depends on the structure of the distribution $\mathcal{D}$ and can be even exponential in the support of $\mathcal{D}$ in many natural scenarios. Our main contribution is to provide an efficient exact sampling algorithm whose complexity does not depend on the structure of $\mathcal{D}$. To this end, we give a parametric Markov chain that mixes significantly faster given a good approximation to the stationary distribution. We can obtain such an approximation using an efficient learning from pairwise comparisons algorithm (Shah et al., JMLR 17, 2016). Our technique for speeding up sampling from a Markov chain whose stationary distribution is approximately known is simple, general and possibly of independent interest.

Differentially Private Regression with Unbounded Covariates

We provide computationally efficient, differentially private algorithms for the classical regression settings of Least Squares Fitting, Binary Regression and Linear Regression with unbounded covariates. Prior to our work, privacy constraints in such regression settings were studied under strong a priori bounds on covariates. We consider the case of Gaussian marginals and extend recent differentially private techniques on mean and covariance estimation (Kamath et al., 2019; Karwa and Vadhan, 2018) to the sub-gaussian regime. We provide a novel technical analysis yielding differentially private algorithms for the above classical regression settings. Through the case of Binary Regression, we capture the fundamental and widely-studied models of logistic regression and linearly-separable SVMs, learning an unbiased estimate of the true regression vector, up to a scaling factor.

Label Ranking through Nonparametric Regression

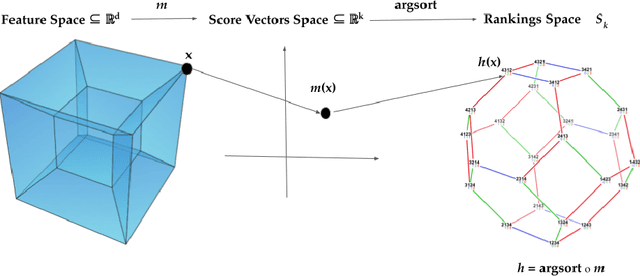
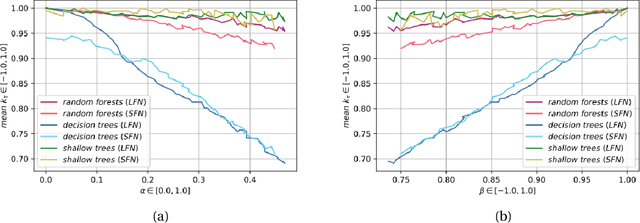
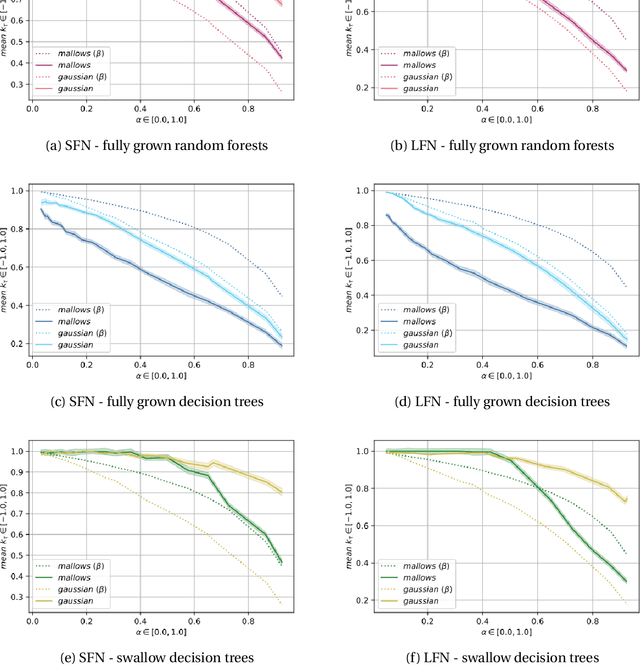
Label Ranking (LR) corresponds to the problem of learning a hypothesis that maps features to rankings over a finite set of labels. We adopt a nonparametric regression approach to LR and obtain theoretical performance guarantees for this fundamental practical problem. We introduce a generative model for Label Ranking, in noiseless and noisy nonparametric regression settings, and provide sample complexity bounds for learning algorithms in both cases. In the noiseless setting, we study the LR problem with full rankings and provide computationally efficient algorithms using decision trees and random forests in the high-dimensional regime. In the noisy setting, we consider the more general cases of LR with incomplete and partial rankings from a statistical viewpoint and obtain sample complexity bounds using the One-Versus-One approach of multiclass classification. Finally, we complement our theoretical contributions with experiments, aiming to understand how the input regression noise affects the observed output.

Efficient Algorithms for Learning from Coarse Labels

For many learning problems one may not have access to fine grained label information; e.g., an image can be labeled as husky, dog, or even animal depending on the expertise of the annotator. In this work, we formalize these settings and study the problem of learning from such coarse data. Instead of observing the actual labels from a set $\mathcal{Z}$, we observe coarse labels corresponding to a partition of $\mathcal{Z}$ (or a mixture of partitions). Our main algorithmic result is that essentially any problem learnable from fine grained labels can also be learned efficiently when the coarse data are sufficiently informative. We obtain our result through a generic reduction for answering Statistical Queries (SQ) over fine grained labels given only coarse labels. The number of coarse labels required depends polynomially on the information distortion due to coarsening and the number of fine labels $|\mathcal{Z}|$. We also investigate the case of (infinitely many) real valued labels focusing on a central problem in censored and truncated statistics: Gaussian mean estimation from coarse data. We provide an efficient algorithm when the sets in the partition are convex and establish that the problem is NP-hard even for very simple non-convex sets.