Partially Trained Graph Convolutional Networks Resist Oversmoothing
Paper and Code
Oct 17, 2024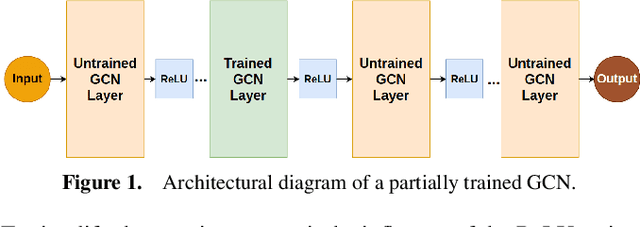
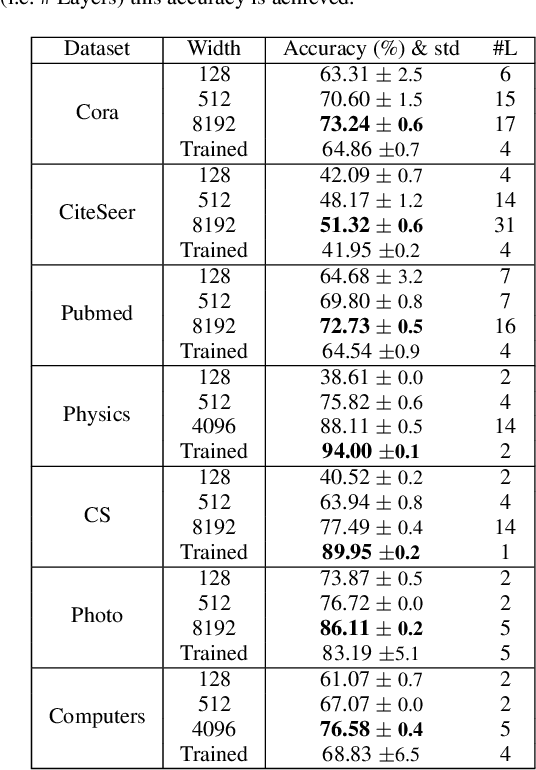


In this work we investigate an observation made by Kipf \& Welling, who suggested that untrained GCNs can generate meaningful node embeddings. In particular, we investigate the effect of training only a single layer of a GCN, while keeping the rest of the layers frozen. We propose a basis on which the effect of the untrained layers and their contribution to the generation of embeddings can be predicted. Moreover, we show that network width influences the dissimilarity of node embeddings produced after the initial node features pass through the untrained part of the model. Additionally, we establish a connection between partially trained GCNs and oversmoothing, showing that they are capable of reducing it. We verify our theoretical results experimentally and show the benefits of using deep networks that resist oversmoothing, in a ``cold start'' scenario, where there is a lack of feature information for unlabeled nodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge