Empirical Bayes for Dynamic Bayesian Networks Using Generalized Variational Inference

In this work, we demonstrate the Empirical Bayes approach to learning a Dynamic Bayesian Network. By starting with several point estimates of structure and weights, we can use a data-driven prior to subsequently obtain a model to quantify uncertainty. This approach uses a recent development of Generalized Variational Inference, and indicates the potential of sampling the uncertainty of a mixture of DAG structures as well as a parameter posterior.

Fairness in Ranking: Robustness through Randomization without the Protected Attribute

There has been great interest in fairness in machine learning, especially in relation to classification problems. In ranking-related problems, such as in online advertising, recommender systems, and HR automation, much work on fairness remains to be done. Two complications arise: first, the protected attribute may not be available in many applications. Second, there are multiple measures of fairness of rankings, and optimization-based methods utilizing a single measure of fairness of rankings may produce rankings that are unfair with respect to other measures. In this work, we propose a randomized method for post-processing rankings, which do not require the availability of the protected attribute. In an extensive numerical study, we show the robustness of our methods with respect to P-Fairness and effectiveness with respect to Normalized Discounted Cumulative Gain (NDCG) from the baseline ranking, improving on previously proposed methods.

Learning quantum Hamiltonians at any temperature in polynomial time with Chebyshev and bit complexity

We consider the problem of learning local quantum Hamiltonians given copies of their Gibbs state at a known inverse temperature, following Haah et al. [2108.04842] and Bakshi et al. [arXiv:2310.02243]. Our main technical contribution is a new flat polynomial approximation of the exponential function based on the Chebyshev expansion, which enables the formulation of learning quantum Hamiltonians as a polynomial optimization problem. This, in turn, can benefit from the use of moment/SOS relaxations, whose polynomial bit complexity requires careful analysis [O'Donnell, ITCS 2017]. Finally, we show that learning a $k$-local Hamiltonian, whose dual interaction graph is of bounded degree, runs in polynomial time under mild assumptions.

Generating Likely Counterfactuals Using Sum-Product Networks

Due to user demand and recent regulation (GDPR, AI Act), decisions made by AI systems need to be explained. These decisions are often explainable only post hoc, where counterfactual explanations are popular. The question of what constitutes the best counterfactual explanation must consider multiple aspects, where "distance from the sample" is the most common. We argue that this requirement frequently leads to explanations that are unlikely and, therefore, of limited value. Here, we present a system that provides high-likelihood explanations. We show that the search for the most likely explanations satisfying many common desiderata for counterfactual explanations can be modeled using mixed-integer optimization (MIO). In the process, we propose an MIO formulation of a Sum-Product Network (SPN) and use the SPN to estimate the likelihood of a counterfactual, which can be of independent interest. A numerical comparison against several methods for generating counterfactual explanations is provided.

Joint Problems in Learning Multiple Dynamical Systems

Clustering of time series is a well-studied problem, with applications ranging from quantitative, personalized models of metabolism obtained from metabolite concentrations to state discrimination in quantum information theory. We consider a variant, where given a set of trajectories and a number of parts, we jointly partition the set of trajectories and learn linear dynamical system (LDS) models for each part, so as to minimize the maximum error across all the models. We present globally convergent methods and EM heuristics, accompanied by promising computational results.

Group-blind optimal transport to group parity and its constrained variants

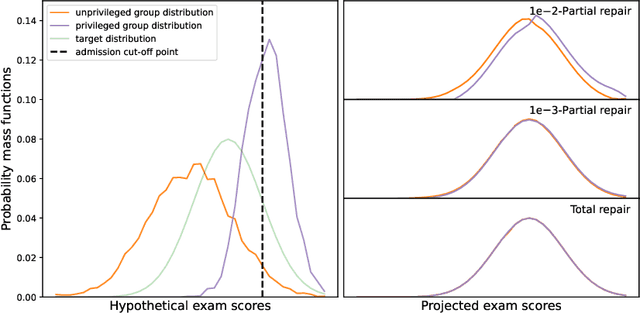
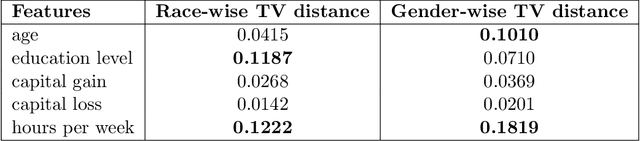
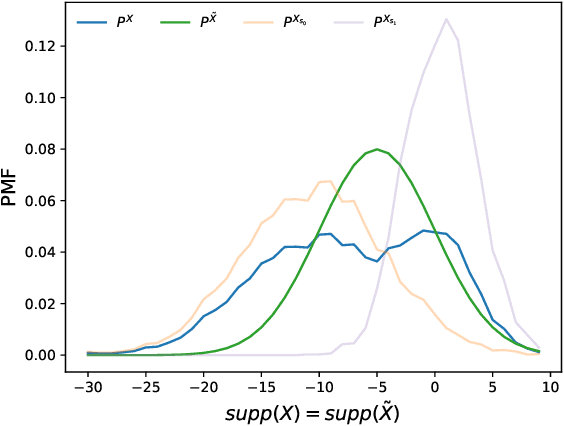
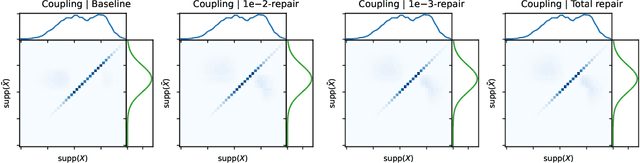
Fairness holds a pivotal role in the realm of machine learning, particularly when it comes to addressing groups categorised by sensitive attributes, e.g., gender, race. Prevailing algorithms in fair learning predominantly hinge on accessibility or estimations of these sensitive attributes, at least in the training process. We design a single group-blind projection map that aligns the feature distributions of both groups in the source data, achieving (demographic) group parity, without requiring values of the protected attribute for individual samples in the computation of the map, as well as its use. Instead, our approach utilises the feature distributions of the privileged and unprivileged groups in a boarder population and the essential assumption that the source data are unbiased representation of the population. We present numerical results on synthetic data and real data.

Taming Binarized Neural Networks and Mixed-Integer Programs

There has been a great deal of recent interest in binarized neural networks, especially because of their explainability. At the same time, automatic differentiation algorithms such as backpropagation fail for binarized neural networks, which limits their applicability. By reformulating the problem of training binarized neural networks as a subadditive dual of a mixed-integer program, we show that binarized neural networks admit a tame representation. This, in turn, makes it possible to use the framework of Bolte et al. for implicit differentiation, which offers the possibility for practical implementation of backpropagation in the context of binarized neural networks. This approach could also be used for a broader class of mixed-integer programs, beyond the training of binarized neural networks, as encountered in symbolic approaches to AI and beyond.

Improving the Validity of Decision Trees as Explanations

In classification and forecasting with tabular data, one often utilizes tree-based models. This can be competitive with deep neural networks on tabular data [cf. Grinsztajn et al., NeurIPS 2022, arXiv:2207.08815] and, under some conditions, explainable. The explainability depends on the depth of the tree and the accuracy in each leaf of the tree. Here, we train a low-depth tree with the objective of minimising the maximum misclassification error across each leaf node, and then ``suspend'' further tree-based models (e.g., trees of unlimited depth) from each leaf of the low-depth tree. The low-depth tree is easily explainable, while the overall statistical performance of the combined low-depth and suspended tree-based models improves upon decision trees of unlimited depth trained using classical methods (e.g., CART) and is comparable to state-of-the-art methods (e.g., well-tuned XGBoost).

Fairness in Forecasting of Observations of Linear Dynamical Systems

In machine learning, training data often capture the behaviour of multiple subgroups of some underlying human population. When the nature of training data for subgroups are not controlled carefully, under-representation bias arises. To counter this effect we introduce two natural notions of subgroup fairness and instantaneous fairness to address such under-representation bias in time-series forecasting problems. Here we show globally convergent methods for the fairness-constrained learning problems using hierarchies of convexifications of non-commutative polynomial optimisation problems. Our empirical results on a biased data set motivated by insurance applications and the well-known COMPAS data set demonstrate the efficacy of our methods. We also show that by exploiting sparsity in the convexifications, we can reduce the run time of our methods considerably.

Closed-Loop View of the Regulation of AI: Equal Impact across Repeated Interactions

There has been much recent interest in the regulation of AI. We argue for a view based on civil-rights legislation, built on the notions of equal treatment and equal impact. In a closed-loop view of the AI system and its users, the equal treatment concerns one pass through the loop. Equal impact, in our view, concerns the long-run average behaviour across repeated interactions. In order to establish the existence of the average and its properties, one needs to study the ergodic properties of the closed-loop and its unique stationary measure.