FORGE: Fused On-Register Gradient Elimination for Memory-Efficient LLM Training

Reverse-mode differentiation computes every weight gradient, writes it to memory, and only then lets the optimizer read it back. This two-phase schedule sets the memory ceiling of modern training: at the seam between the phases, every layer's gradient is live at once. We argue that this materialized gradient is an artifact of how differentiation is staged, not a quantity that learning requires -- and we eliminate it. FORGE folds the optimizer step into the backward pass and applies it one tile at a time, entirely in registers, so each gradient tile is consumed the instant it is produced and never becomes a tensor. The fusion changes only when the update happens, not what it computes: in full precision the fused step is provably exact -- the identical optimizer update, for every element-wise rule -- and that exactness survives tensor- and sequence-parallel sharding; in the bf16 and 8-bit regimes used in practice it is faithful rather than bit-identical, its deviation bounded and, for the weight store, rendered unbiased by stochastic rounding. Because each gradient tile is born and consumed in the same registers, it is never converted down to bf16 to be stored and read back; FORGE thus preserves the full-precision fidelity that both bf16 and 8-bit optimizers lose to that conversion. Nor is the method tied to one architecture or one optimizer: linear layers are ubiquitous, and FORGE reclaims the gradient memory of any of them under any element-wise rule. Empirically FORGE more than halves the memory of an optimizer step and, at the small batch sizes typical of fine-tuning and continued pretraining, runs about 1.5x faster; integrated into tensor-parallel Megatron-LM it fits 8B training at four times the micro-batch a standard optimizer allows on the same GPUs.

Federated Instrumental Variable Analysis via Federated Generalized Method of Moments

Instrumental variables (IV) analysis is an important applied tool for areas such as healthcare and consumer economics. For IV analysis in high-dimensional settings, the Generalized Method of Moments (GMM) using deep neural networks offers an efficient approach. With non-i.i.d. data sourced from scattered decentralized clients, federated learning is a popular paradigm for training the models while promising data privacy. However, to our knowledge, no federated algorithm for either GMM or IV analysis exists to date. In this work, we introduce federated instrumental variables analysis (FedIV) via federated generalized method of moments (FedGMM). We formulate FedGMM as a federated zero-sum game defined by a federated non-convex non-concave minimax optimization problem, which is solved using federated gradient descent ascent (FedGDA) algorithm. One key challenge arises in theoretically characterizing the federated local optimality. To address this, we present properties and existence results of clients' local equilibria via FedGDA limit points. Thereby, we show that the federated solution consistently estimates the local moment conditions of every participating client. The proposed algorithm is backed by extensive experiments to demonstrate the efficacy of our approach.

Towards Hyper-parameter-free Federated Learning

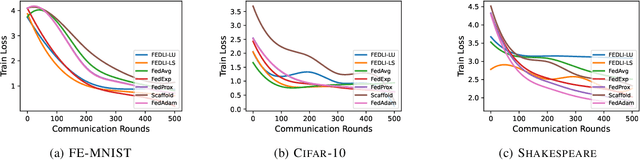
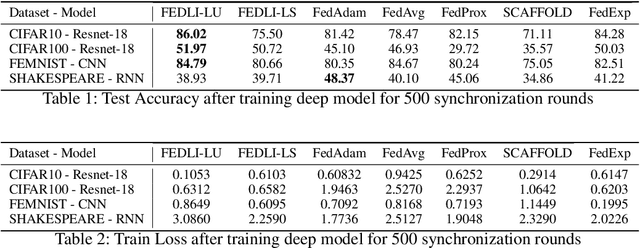
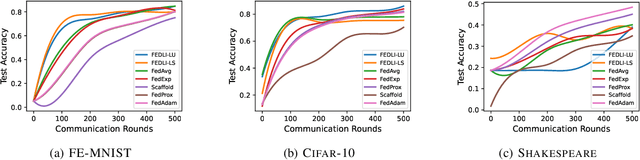
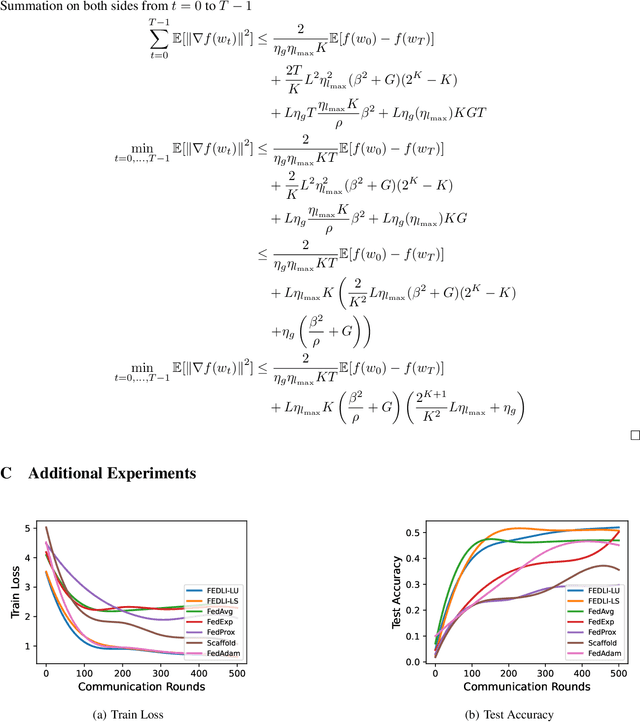
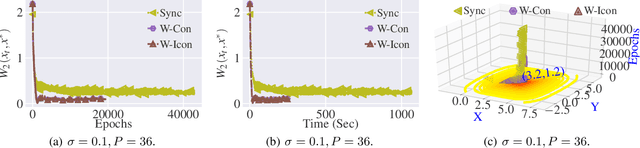
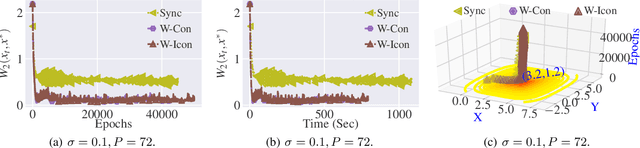
The adaptive synchronization techniques in federated learning (FL) for scaled global model updates show superior performance over the vanilla federated averaging (FedAvg) scheme. However, existing methods employ additional tunable hyperparameters on the server to determine the scaling factor. A contrasting approach is automated scaling analogous to tuning-free step-size schemes in stochastic gradient descent (SGD) methods, which offer competitive convergence rates and exhibit good empirical performance. In this work, we introduce two algorithms for automated scaling of global model updates. In our first algorithm, we establish that a descent-ensuring step-size regime at the clients ensures descent for the server objective. We show that such a scheme enables linear convergence for strongly convex federated objectives. Our second algorithm shows that the average of objective values of sampled clients is a practical and effective substitute for the objective function value at the server required for computing the scaling factor, whose computation is otherwise not permitted. Our extensive empirical results show that the proposed methods perform at par or better than the popular federated learning algorithms for both convex and non-convex problems. Our work takes a step towards designing hyper-parameter-free federated learning.

Empirical Bayes for Dynamic Bayesian Networks Using Generalized Variational Inference

In this work, we demonstrate the Empirical Bayes approach to learning a Dynamic Bayesian Network. By starting with several point estimates of structure and weights, we can use a data-driven prior to subsequently obtain a model to quantify uncertainty. This approach uses a recent development of Generalized Variational Inference, and indicates the potential of sampling the uncertainty of a mixture of DAG structures as well as a parameter posterior.

Scaling the Wild: Decentralizing Hogwild!-style Shared-memory SGD

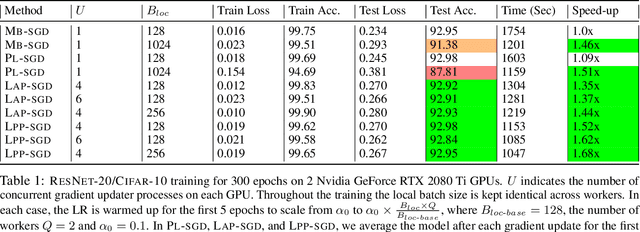
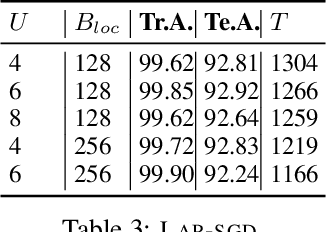
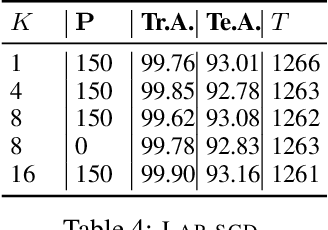
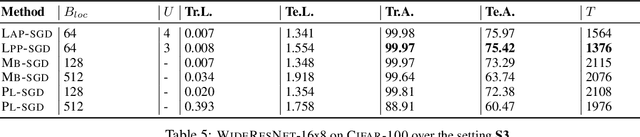
Powered by the simplicity of lock-free asynchrony, Hogwilld! is a go-to approach to parallelize SGD over a shared-memory setting. Despite its popularity and concomitant extensions, such as PASSM+ wherein concurrent processes update a shared model with partitioned gradients, scaling it to decentralized workers has surprisingly been relatively unexplored. To our knowledge, there is no convergence theory of such methods, nor systematic numerical comparisons evaluating speed-up. In this paper, we propose an algorithm incorporating decentralized distributed memory computing architecture with each node running multiprocessing parallel shared-memory SGD itself. Our scheme is based on the following algorithmic tools and features: (a) asynchronous local gradient updates on the shared-memory of workers, (b) partial backpropagation, and (c) non-blocking in-place averaging of the local models. We prove that our method guarantees ergodic convergence rates for non-convex objectives. On the practical side, we show that the proposed method exhibits improved throughput and competitive accuracy for standard image classification benchmarks on the CIFAR-10, CIFAR-100, and Imagenet datasets. Our code is available at https://github.com/bapi/LPP-SGD.

Stochastic Gradient Langevin with Delayed Gradients

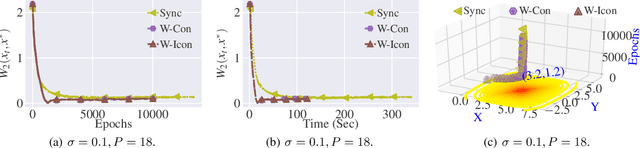
Stochastic Gradient Langevin Dynamics (SGLD) ensures strong guarantees with regards to convergence in measure for sampling log-concave posterior distributions by adding noise to stochastic gradient iterates. Given the size of many practical problems, parallelizing across several asynchronously running processors is a popular strategy for reducing the end-to-end computation time of stochastic optimization algorithms. In this paper, we are the first to investigate the effect of asynchronous computation, in particular, the evaluation of stochastic Langevin gradients at delayed iterates, on the convergence in measure. For this, we exploit recent results modeling Langevin dynamics as solving a convex optimization problem on the space of measures. We show that the rate of convergence in measure is not significantly affected by the error caused by the delayed gradient information used for computation, suggesting significant potential for speedup in wall clock time. We confirm our theoretical results with numerical experiments on some practical problems.

Elastic Consistency: A General Consistency Model for Distributed Stochastic Gradient Descent

Machine learning has made tremendous progress in recent years, with models matching or even surpassing humans on a series of specialized tasks. One key element behind the progress of machine learning in recent years has been the ability to train machine learning models in large-scale distributed shared-memory and message-passing environments. Many of these models are trained employing variants of stochastic gradient descent (SGD) based optimization. In this paper, we introduce a general consistency condition covering communication-reduced and asynchronous distributed SGD implementations. Our framework, called elastic consistency enables us to derive convergence bounds for a variety of distributed SGD methods used in practice to train large-scale machine learning models. The proposed framework de-clutters the implementation-specific convergence analysis and provides an abstraction to derive convergence bounds. We utilize the framework to analyze a sparsification scheme for distributed SGD methods in an asynchronous setting for convex and non-convex objectives. We implement the distributed SGD variant to train deep CNN models in an asynchronous shared-memory setting. Empirical results show that error-feedback may not necessarily help in improving the convergence of sparsified asynchronous distributed SGD, which corroborates an insight suggested by our convergence analysis.