Stochastic Gradient Langevin with Delayed Gradients

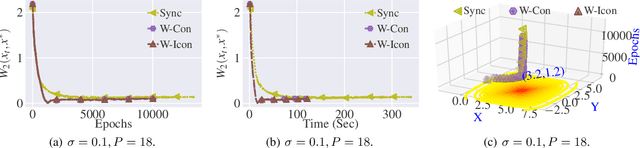
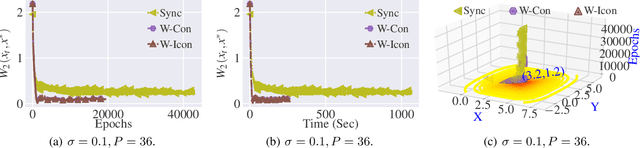
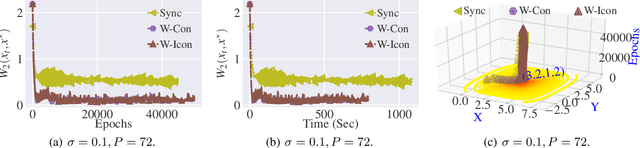
Stochastic Gradient Langevin Dynamics (SGLD) ensures strong guarantees with regards to convergence in measure for sampling log-concave posterior distributions by adding noise to stochastic gradient iterates. Given the size of many practical problems, parallelizing across several asynchronously running processors is a popular strategy for reducing the end-to-end computation time of stochastic optimization algorithms. In this paper, we are the first to investigate the effect of asynchronous computation, in particular, the evaluation of stochastic Langevin gradients at delayed iterates, on the convergence in measure. For this, we exploit recent results modeling Langevin dynamics as solving a convex optimization problem on the space of measures. We show that the rate of convergence in measure is not significantly affected by the error caused by the delayed gradient information used for computation, suggesting significant potential for speedup in wall clock time. We confirm our theoretical results with numerical experiments on some practical problems.