Dan Alistarh
LoRDO: Distributed Low-Rank Optimization with Infrequent Communication
Feb 04, 2026Abstract:Distributed training of foundation models via $\texttt{DDP}$ is limited by interconnect bandwidth. While infrequent communication strategies reduce synchronization frequency, they remain bottlenecked by the memory and communication requirements of optimizer states. Low-rank optimizers can alleviate these constraints; however, in the local-update regime, workers lack access to the full-batch gradients required to compute low-rank projections, which degrades performance. We propose $\texttt{LoRDO}$, a principled framework unifying low-rank optimization with infrequent synchronization. We first demonstrate that, while global projections based on pseudo-gradients are theoretically superior, they permanently restrict the optimization trajectory to a low-rank subspace. To restore subspace exploration, we introduce a full-rank quasi-hyperbolic update. $\texttt{LoRDO}$ achieves near-parity with low-rank $\texttt{DDP}$ in language modeling and downstream tasks at model scales of $125$M--$720$M, while reducing communication by $\approx 10 \times$. Finally, we show that $\texttt{LoRDO}$ improves performance even more in very low-memory settings with small rank/batch size.
MatGPTQ: Accurate and Efficient Post-Training Matryoshka Quantization
Feb 03, 2026Abstract:Matryoshka Quantization (MatQuant) is a recent quantization approach showing that a single integer-quantized model can be served across multiple precisions, by slicing the most significant bits (MSB) at inference time. This enables a single checkpoint to cover a wide range of memory and latency budgets, but renders quantization much more challenging. In particular, the initial MatQuant relies on expensive quantization-aware training (QAT) variants, rather than fast one-shot post training quantization (PTQ), and lacks open-source and kernel support. We address all of these limitations by introducing Post-Training Matryoshka Quantization (MatGPTQ), a new PTQ pipeline that produces a single parent model jointly optimized for multiple target precisions in one-shot, based on a small calibration set. MatGPTQ casts Matryoshka quantization as a multi-precision objective with bit-slicing and cross-bit error compensation, resulting in an algorithm that produces a multi-bit-width, "sliceable" model in a single pass. We also incorporate a new budget-aware search for heterogeneous per-layer bit-witdhs and provide efficient kernels that implement slicing and mixed-precision execution. Across standard LLMs and benchmarks, MatGPTQ preserves high-bit accuracy while substantially improving performance at low-bit-witdh settings. Overall, we establish a new state of the art for Matryoshka-style post-training quantization and make single-checkpoint, multi-precision deployment open and practical. Code is available at https://github.com/IST-DASLab/MatGPTQ.
DASH: Faster Shampoo via Batched Block Preconditioning and Efficient Inverse-Root Solvers
Feb 02, 2026Abstract:Shampoo is one of the leading approximate second-order optimizers: a variant of it has won the MLCommons AlgoPerf competition, and it has been shown to produce models with lower activation outliers that are easier to compress. Yet, applying Shampoo currently comes at the cost of significant computational slowdown, due to its expensive internal operations. In this paper, we take a significant step to address this shortcoming by proposing \method (for \textbf{D}istributed \textbf{A}ccelerated \textbf{SH}ampoo), a faster implementation of Distributed Shampoo based on two main new techniques: First, we show that preconditioner blocks can be stacked into 3D tensors to significantly improve GPU utilization; second, we introduce the Newton-DB iteration and the Chebyshev polynomial approximations as novel and faster approaches for computing the inverse matrix roots required by Shampoo. Along with these algorithmic contributions, we provide a first in-depth analysis of how matrix scaling critically affects Shampoo convergence. On the practical side, our GPU-aware implementation achieves up to $4.83\times$ faster optimizer steps compared to the well-optimized Distributed Shampoo, while Newton-DB attains the lowest validation perplexity per iteration among all tested methods. Our code is available at https://github.com/IST-DASLab/DASH.
Behemoth: Benchmarking Unlearning in LLMs Using Fully Synthetic Data
Jan 30, 2026Abstract:As artificial neural networks, and specifically large language models, have improved rapidly in capabilities and quality, they have increasingly been deployed in real-world applications, from customer service to Google search, despite the fact that they frequently make factually incorrect or undesirable statements. This trend has inspired practical and academic interest in model editing, that is, in adjusting the weights of the model to modify its likely outputs for queries relating to a specific fact or set of facts. This may be done either to amend a fact or set of facts, for instance, to fix a frequent error in the training data, or to suppress a fact or set of facts entirely, for instance, in case of dangerous knowledge. Multiple methods have been proposed to do such edits. However, at the same time, it has been shown that such model editing can be brittle and incomplete. Moreover the effectiveness of any model editing method necessarily depends on the data on which the model is trained, and, therefore, a good understanding of the interaction of the training data distribution and the way it is stored in the network is necessary and helpful to reliably perform model editing. However, working with large language models trained on real-world data does not allow us to understand this relationship or fully measure the effects of model editing. We therefore propose Behemoth, a fully synthetic data generation framework. To demonstrate the practical insights from the framework, we explore model editing in the context of simple tabular data, demonstrating surprising findings that, in some cases, echo real-world results, for instance, that in some cases restricting the update rank results in a more effective update. The code is available at https://github.com/IST-DASLab/behemoth.git.
Quartet II: Accurate LLM Pre-Training in NVFP4 by Improved Unbiased Gradient Estimation
Jan 30, 2026Abstract:The NVFP4 lower-precision format, supported in hardware by NVIDIA Blackwell GPUs, promises to allow, for the first time, end-to-end fully-quantized pre-training of massive models such as LLMs. Yet, existing quantized training methods still sacrifice some of the representation capacity of this format in favor of more accurate unbiased quantized gradient estimation by stochastic rounding (SR), losing noticeable accuracy relative to standard FP16 and FP8 training. In this paper, improve the state of the art for quantized training in NVFP4 via a novel unbiased quantization routine for micro-scaled formats, called MS-EDEN, that has more than 2x lower quantization error than SR. We integrate it into a novel fully-NVFP4 quantization scheme for linear layers, called Quartet II. We show analytically that Quartet II achieves consistently better gradient estimation across all major matrix multiplications, both on the forward and on the backward passes. In addition, our proposal synergizes well with recent training improvements aimed specifically at NVFP4. We further validate Quartet II on end-to-end LLM training with up to 1.9B parameters on 38B tokens. We provide kernels for execution on NVIDIA Blackwell GPUs with up to 4.2x speedup over BF16. Our code is available at https://github.com/IST-DASLab/Quartet-II .
ECO: Quantized Training without Full-Precision Master Weights
Jan 29, 2026Abstract:Quantization has significantly improved the compute and memory efficiency of Large Language Model (LLM) training. However, existing approaches still rely on accumulating their updates in high-precision: concretely, gradient updates must be applied to a high-precision weight buffer, known as $\textit{master weights}$. This buffer introduces substantial memory overhead, particularly for Sparse Mixture of Experts (SMoE) models, where model parameters and optimizer states dominate memory usage. To address this, we introduce the Error-Compensating Optimizer (ECO), which eliminates master weights by applying updates directly to quantized parameters. ECO quantizes weights after each step and carefully injects the resulting quantization error into the optimizer momentum, forming an error-feedback loop with no additional memory. We prove that, under standard assumptions and a decaying learning rate, ECO converges to a constant-radius neighborhood of the optimum, while naive master-weight removal can incur an error that is inversely proportional to the learning rate. We show empirical results for pretraining small Transformers (30-800M), a Gemma-3 1B model, and a 2.1B parameter Sparse MoE model with FP8 quantization, and fine-tuning DeepSeek-MoE-16B in INT4 precision. Throughout, ECO matches baselines with master weights up to near-lossless accuracy, significantly shifting the static memory vs validation loss Pareto frontier.
LLMQ: Efficient Lower-Precision Pretraining for Consumer GPUs
Dec 17, 2025Abstract:We present LLMQ, an end-to-end CUDA/C++ implementation for medium-sized language-model training, e.g. 3B to 32B parameters, on affordable, commodity GPUs. These devices are characterized by low memory availability and slow communication compared to datacentre-grade GPUs. Consequently, we showcase a range of optimizations that target these bottlenecks, including activation checkpointing, offloading, and copy-engine based collectives. LLMQ is able to train or fine-tune a 7B model on a single 16GB mid-range gaming card, or a 32B model on a workstation equipped with 4 RTX 4090s. This is achieved while executing a standard 8-bit training pipeline, without additional algorithmic approximations, and maintaining FLOP utilization of around 50%. The efficiency of LLMQ rivals that of production-scale systems on much more expensive cloud-grade GPUs.
Speculative Decoding Speed-of-Light: Optimal Lower Bounds via Branching Random Walks
Dec 12, 2025Abstract:Speculative generation has emerged as a promising technique to accelerate inference in large language models (LLMs) by leveraging parallelism to verify multiple draft tokens simultaneously. However, the fundamental limits on the achievable speedup remain poorly understood. In this work, we establish the first ``tight'' lower bounds on the runtime of any deterministic speculative generation algorithm. This is achieved by drawing a parallel between the token generation process and branching random walks, which allows us to analyze the optimal draft tree selection problem. We prove, under basic assumptions, that the expected number of tokens successfully predicted per speculative iteration is bounded as $\mathbb{E}[X] \leq (μ+ μ_{(2)})\log(P )/μ^2 + O(1)$, where $P$ is the verifier's capacity, $μ$ is the expected entropy of the verifier's output distribution, and $μ_{(2)}$ is the expected second log-moment. This result provides new insights into the limits of parallel token generation, and could guide the design of future speculative decoding systems. Empirical evaluations on Llama models validate our theoretical predictions, confirming the tightness of our bounds in practical settings.
Expand Neurons, Not Parameters
Oct 06, 2025
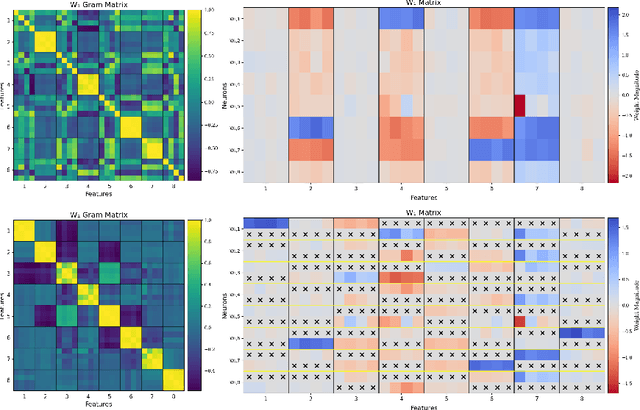
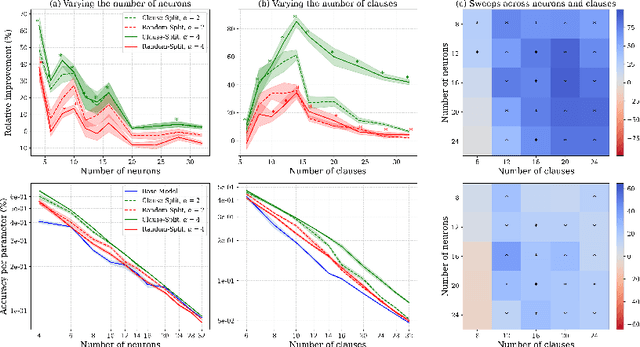
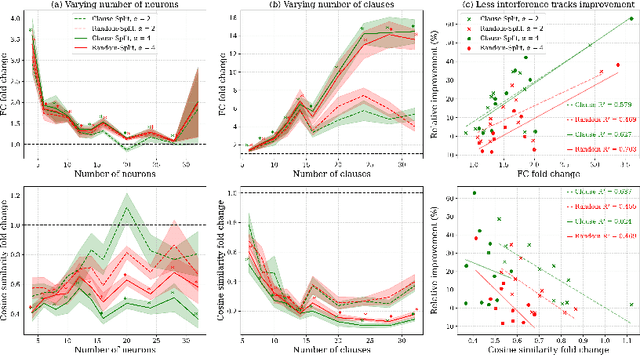
Abstract:This work demonstrates how increasing the number of neurons in a network without increasing its number of non-zero parameters improves performance. We show that this gain corresponds with a decrease in interference between multiple features that would otherwise share the same neurons. To reduce such entanglement at a fixed non-zero parameter count, we introduce Fixed Parameter Expansion (FPE): replace a neuron with multiple children and partition the parent's weights disjointly across them, so that each child inherits a non-overlapping subset of connections. On symbolic tasks, specifically Boolean code problems, clause-aligned FPE systematically reduces polysemanticity metrics and yields higher task accuracy. Notably, random splits of neuron weights approximate these gains, indicating that reduced collisions, not precise assignment, are a primary driver. Consistent with the superposition hypothesis, the benefits of FPE grow with increasing interference: when polysemantic load is high, accuracy improvements are the largest. Transferring these insights to real models (classifiers over CLIP embeddings and deeper multilayer networks) we find that widening networks while maintaining a constant non-zero parameter count consistently increases accuracy. These results identify an interpretability-grounded mechanism to leverage width against superposition, improving performance without increasing the number of non-zero parameters. Such a direction is well matched to modern accelerators, where memory movement of non-zero parameters, rather than raw compute, is the dominant bottleneck.
The Unseen Frontier: Pushing the Limits of LLM Sparsity with Surrogate-Free ADMM
Oct 02, 2025Abstract:Neural network pruning is a promising technique to mitigate the excessive computational and memory requirements of large language models (LLMs). Despite its promise, however, progress in this area has diminished, as conventional methods are seemingly unable to surpass moderate sparsity levels (50-60%) without severely degrading model accuracy. This work breaks through the current impasse, presenting a principled and effective method called $\texttt{Elsa}$, which achieves extreme sparsity levels of up to 90% while retaining high model fidelity. This is done by identifying several limitations in current practice, all of which can be traced back to their reliance on a surrogate objective formulation. $\texttt{Elsa}$ tackles this issue directly and effectively via standard and well-established constrained optimization techniques based on ADMM. Our extensive experiments across a wide range of models and scales show that $\texttt{Elsa}$ achieves substantial improvements over existing methods; e.g., it achieves 7.8$\times$ less perplexity than the best existing method on LLaMA-2-7B at 90% sparsity. Furthermore, we present $\texttt{Elsa}_{\text{-L}}$, a quantized variant that scales to extremely large models (27B), and establish its theoretical convergence guarantees. These results highlight meaningful progress in advancing the frontier of LLM sparsity, while promising that significant opportunities for further advancement may remain in directions that have so far attracted limited exploration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge