Towards Combinatorial Interpretability of Neural Computation
Paper and Code
Apr 10, 2025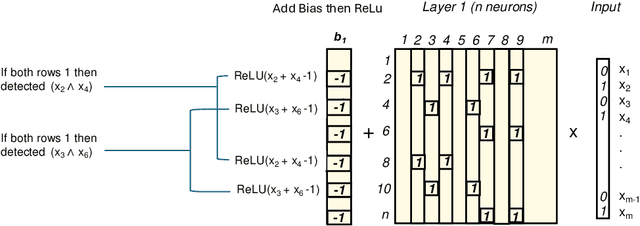

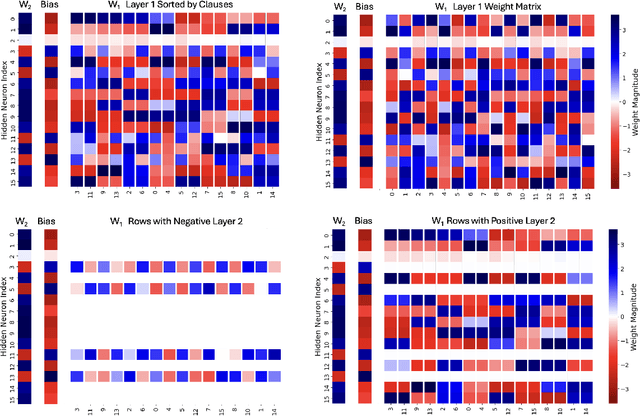
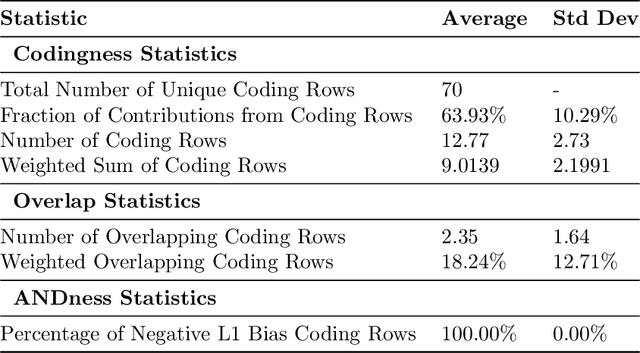
We introduce combinatorial interpretability, a methodology for understanding neural computation by analyzing the combinatorial structures in the sign-based categorization of a network's weights and biases. We demonstrate its power through feature channel coding, a theory that explains how neural networks compute Boolean expressions and potentially underlies other categories of neural network computation. According to this theory, features are computed via feature channels: unique cross-neuron encodings shared among the inputs the feature operates on. Because different feature channels share neurons, the neurons are polysemantic and the channels interfere with one another, making the computation appear inscrutable. We show how to decipher these computations by analyzing a network's feature channel coding, offering complete mechanistic interpretations of several small neural networks that were trained with gradient descent. Crucially, this is achieved via static combinatorial analysis of the weight matrices, without examining activations or training new autoencoding networks. Feature channel coding reframes the superposition hypothesis, shifting the focus from neuron activation directionality in high-dimensional space to the combinatorial structure of codes. It also allows us for the first time to exactly quantify and explain the relationship between a network's parameter size and its computational capacity (i.e. the set of features it can compute with low error), a relationship that is implicitly at the core of many modern scaling laws. Though our initial studies of feature channel coding are restricted to Boolean functions, we believe they provide a rich, controlled, and informative research space, and that the path we propose for combinatorial interpretation of neural computation can provide a basis for understanding both artificial and biological neural circuits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge