BiCoLoR: Communication-Efficient Optimization with Bidirectional Compression and Local Training

Slow and costly communication is often the main bottleneck in distributed optimization, especially in federated learning where it occurs over wireless networks. We introduce BiCoLoR, a communication-efficient optimization algorithm that combines two widely used and effective strategies: local training, which increases computation between communication rounds, and compression, which encodes high-dimensional vectors into short bitstreams. While these mechanisms have been combined before, compression has typically been applied only to uplink (client-to-server) communication, leaving the downlink (server-to-client) side unaddressed. In practice, however, both directions are costly. We propose BiCoLoR, the first algorithm to combine local training with bidirectional compression using arbitrary unbiased compressors. This joint design achieves accelerated complexity guarantees in both convex and strongly convex heterogeneous settings. Empirically, BiCoLoR outperforms existing algorithms and establishes a new standard in communication efficiency.

First Provable Guarantees for Practical Private FL: Beyond Restrictive Assumptions

Federated Learning (FL) enables collaborative training on decentralized data. Differential privacy (DP) is crucial for FL, but current private methods often rely on unrealistic assumptions (e.g., bounded gradients or heterogeneity), hindering practical application. Existing works that relax these assumptions typically neglect practical FL features, including multiple local updates and partial client participation. We introduce Fed-$α$-NormEC, the first differentially private FL framework providing provable convergence and DP guarantees under standard assumptions while fully supporting these practical features. Fed-$α$-NormE integrates local updates (full and incremental gradient steps), separate server and client stepsizes, and, crucially, partial client participation, which is essential for real-world deployment and vital for privacy amplification. Our theoretical guarantees are corroborated by experiments on private deep learning tasks.

Muon is Provably Faster with Momentum Variance Reduction

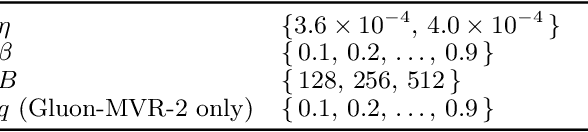
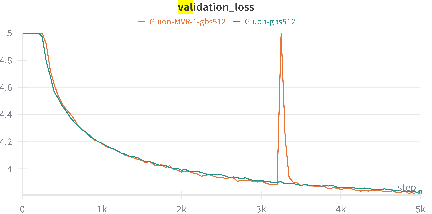
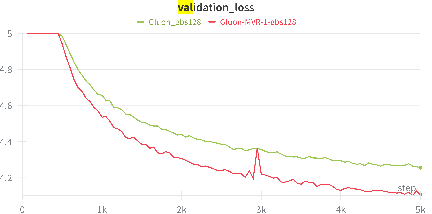
Recent empirical research has demonstrated that deep learning optimizers based on the linear minimization oracle (LMO) over specifically chosen Non-Euclidean norm balls, such as Muon and Scion, outperform Adam-type methods in the training of large language models. In this work, we show that such optimizers can be provably improved by replacing their vanilla momentum by momentum variance reduction (MVR). Instead of proposing and analyzing MVR variants of Muon and Scion separately, we incorporate MVR into the recently proposed Gluon framework, which captures Muon, Scion and other specific Non-Euclidean LMO-based methods as special cases, and at the same time works with a more general smoothness assumption which better captures the layer-wise structure of neural networks. In the non-convex case, we incorporate MVR into Gluon in three different ways. All of them improve the convergence rate from ${\cal O} (\frac{1}{K^{1/4}})$ to ${\cal O} (\frac{1}{K^{1/3}})$. Additionally, we provide improved rates in the star-convex case. Finally, we conduct several numerical experiments that verify the superior performance of our proposed algorithms in terms of iteration complexity.

Better LMO-based Momentum Methods with Second-Order Information

The use of momentum in stochastic optimization algorithms has shown empirical success across a range of machine learning tasks. Recently, a new class of stochastic momentum algorithms has emerged within the Linear Minimization Oracle (LMO) framework--leading to state-of-the-art methods, such as Muon, Scion, and Gluon, that effectively solve deep neural network training problems. However, traditional stochastic momentum methods offer convergence guarantees no better than the ${O}(1/K^{1/4})$ rate. While several approaches--such as Hessian-Corrected Momentum (HCM)--have aimed to improve this rate, their theoretical results are generally restricted to the Euclidean norm setting. This limitation hinders their applicability in problems, where arbitrary norms are often required. In this paper, we extend the LMO-based framework by integrating HCM, and provide convergence guarantees under relaxed smoothness and arbitrary norm settings. We establish improved convergence rates of ${O}(1/K^{1/3})$ for HCM, which can adapt to the geometry of the problem and achieve a faster rate than traditional momentum. Experimental results on training Multi-Layer Perceptrons (MLPs) and Long Short-Term Memory (LSTM) networks verify our theoretical observations.

Improved Convergence in Parameter-Agnostic Error Feedback through Momentum

Communication compression is essential for scalable distributed training of modern machine learning models, but it often degrades convergence due to the noise it introduces. Error Feedback (EF) mechanisms are widely adopted to mitigate this issue of distributed compression algorithms. Despite their popularity and training efficiency, existing distributed EF algorithms often require prior knowledge of problem parameters (e.g., smoothness constants) to fine-tune stepsizes. This limits their practical applicability especially in large-scale neural network training. In this paper, we study normalized error feedback algorithms that combine EF with normalized updates, various momentum variants, and parameter-agnostic, time-varying stepsizes, thus eliminating the need for problem-dependent tuning. We analyze the convergence of these algorithms for minimizing smooth functions, and establish parameter-agnostic complexity bounds that are close to the best-known bounds with carefully-tuned problem-dependent stepsizes. Specifically, we show that normalized EF21 achieve the convergence rate of near ${O}(1/T^{1/4})$ for Polyak's heavy-ball momentum, ${O}(1/T^{2/7})$ for Iterative Gradient Transport (IGT), and ${O}(1/T^{1/3})$ for STORM and Hessian-corrected momentum. Our results hold with decreasing stepsizes and small mini-batches. Finally, our empirical experiments confirm our theoretical insights.

Drop-Muon: Update Less, Converge Faster

Conventional wisdom in deep learning optimization dictates updating all layers at every step-a principle followed by all recent state-of-the-art optimizers such as Muon. In this work, we challenge this assumption, showing that full-network updates can be fundamentally suboptimal, both in theory and in practice. We introduce a non-Euclidean Randomized Progressive Training method-Drop-Muon-a simple yet powerful framework that updates only a subset of layers per step according to a randomized schedule, combining the efficiency of progressive training with layer-specific non-Euclidean updates for top-tier performance. We provide rigorous convergence guarantees under both layer-wise smoothness and layer-wise $(L^0, L^1)$-smoothness, covering deterministic and stochastic gradient settings, marking the first such results for progressive training in the stochastic and non-smooth regime. Our cost analysis further reveals that full-network updates are not optimal unless a very specific relationship between layer smoothness constants holds. Through controlled CNN experiments, we empirically demonstrate that Drop-Muon consistently outperforms full-network Muon, achieving the same accuracy up to $1.4\times$ faster in wall-clock time. Together, our results suggest a shift in how large-scale models can be efficiently trained, challenging the status quo and offering a highly efficient, theoretically grounded alternative to full-network updates.

Error Feedback for Muon and Friends

Recent optimizers like Muon, Scion, and Gluon have pushed the frontier of large-scale deep learning by exploiting layer-wise linear minimization oracles (LMOs) over non-Euclidean norm balls, capturing neural network structure in ways traditional algorithms cannot. Yet, no principled distributed framework exists for these methods, and communication bottlenecks remain unaddressed. The very few distributed variants are heuristic, with no convergence guarantees in sight. We introduce EF21-Muon, the first communication-efficient, non-Euclidean LMO-based optimizer with rigorous convergence guarantees. EF21-Muon supports stochastic gradients, momentum, and bidirectional compression with error feedback-marking the first extension of error feedback beyond the Euclidean setting. It recovers Muon/Scion/Gluon when compression is off and specific norms are chosen, providing the first efficient distributed implementation of this powerful family. Our theory covers non-Euclidean smooth and the more general $(L^0, L^1)$-smooth setting, matching best-known Euclidean rates and enabling faster convergence under suitable norm choices. We further extend the analysis to layer-wise (generalized) smoothness regimes, capturing the anisotropic structure of deep networks. Experiments on NanoGPT benchmarking EF21-Muon against uncompressed Muon/Scion/Gluon demonstrate up to $7\times$ communication savings with no accuracy degradation.

Non-Euclidean Broximal Point Method: A Blueprint for Geometry-Aware Optimization

The recently proposed Broximal Point Method (BPM) [Gruntkowska et al., 2025] offers an idealized optimization framework based on iteratively minimizing the objective function over norm balls centered at the current iterate. It enjoys striking global convergence guarantees, converging linearly and in a finite number of steps for proper, closed and convex functions. However, its theoretical analysis has so far been confined to the Euclidean geometry. At the same time, emerging trends in deep learning optimization, exemplified by algorithms such as Muon [Jordan et al., 2024] and Scion [Pethick et al., 2025], demonstrate the practical advantages of minimizing over balls defined via non-Euclidean norms which better align with the underlying geometry of the associated loss landscapes. In this note, we ask whether the convergence theory of BPM can be extended to this more general, non-Euclidean setting. We give a positive answer, showing that most of the elegant guarantees of the original method carry over to arbitrary norm geometries. Along the way, we clarify which properties are preserved and which necessarily break down when leaving the Euclidean realm. Our analysis positions Non-Euclidean BPM as a conceptual blueprint for understanding a broad class of geometry-aware optimization algorithms, shedding light on the principles behind their practical effectiveness.

Gluon: Making Muon & Scion Great Again! (Bridging Theory and Practice of LMO-based Optimizers for LLMs)

Recent developments in deep learning optimization have brought about radically new algorithms based on the Linear Minimization Oracle (LMO) framework, such as $\sf Muon$ and $\sf Scion$. After over a decade of $\sf Adam$'s dominance, these LMO-based methods are emerging as viable replacements, offering several practical advantages such as improved memory efficiency, better hyperparameter transferability, and most importantly, superior empirical performance on large-scale tasks, including LLM training. However, a significant gap remains between their practical use and our current theoretical understanding: prior analyses (1) overlook the layer-wise LMO application of these optimizers in practice, and (2) rely on an unrealistic smoothness assumption, leading to impractically small stepsizes. To address both, we propose a new LMO-based method called $\sf Gluon$, capturing prior theoretically analyzed methods as special cases, and introduce a new refined generalized smoothness model that captures the layer-wise geometry of neural networks, matches the layer-wise practical implementation of $\sf Muon$ and $\sf Scion$, and leads to convergence guarantees with strong practical predictive power. Unlike prior results, our theoretical stepsizes closely match the fine-tuned values reported by Pethick et al. (2025). Our experiments with NanoGPT and CNN confirm that our assumption holds along the optimization trajectory, ultimately closing the gap between theory and practice.

BurTorch: Revisiting Training from First Principles by Coupling Autodiff, Math Optimization, and Systems

In this work, we introduce BurTorch, a compact high-performance framework designed to optimize Deep Learning (DL) training on single-node workstations through an exceptionally efficient CPU-based backpropagation (Rumelhart et al., 1986; Linnainmaa, 1970) implementation. Although modern DL frameworks rely on compilerlike optimizations internally, BurTorch takes a different path. It adopts a minimalist design and demonstrates that, in these circumstances, classical compiled programming languages can play a significant role in DL research. By eliminating the overhead of large frameworks and making efficient implementation choices, BurTorch achieves orders-of-magnitude improvements in performance and memory efficiency when computing $\nabla f(x)$ on a CPU. BurTorch features a compact codebase designed to achieve two key goals simultaneously. First, it provides a user experience similar to script-based programming environments. Second, it dramatically minimizes runtime overheads. In large DL frameworks, the primary source of memory overhead for relatively small computation graphs $f(x)$ is due to feature-heavy implementations. We benchmarked BurTorch against widely used DL frameworks in their execution modes: JAX (Bradbury et al., 2018), PyTorch (Paszke et al., 2019), TensorFlow (Abadi et al., 2016); and several standalone libraries: Autograd (Maclaurin et al., 2015), Micrograd (Karpathy, 2020), Apple MLX (Hannun et al., 2023). For small compute graphs, BurTorch outperforms best-practice solutions by up to $\times 2000$ in runtime and reduces memory consumption by up to $\times 3500$. For a miniaturized GPT-3 model (Brown et al., 2020), BurTorch achieves up to a $\times 20$ speedup and reduces memory up to $\times 80$ compared to PyTorch.