Dynamic N:M Fine-grained Structured Sparse Attention Mechanism

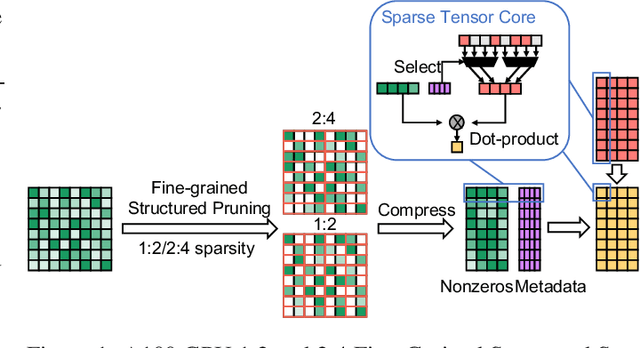
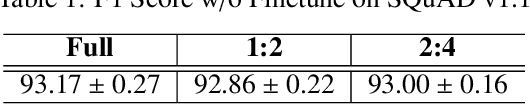
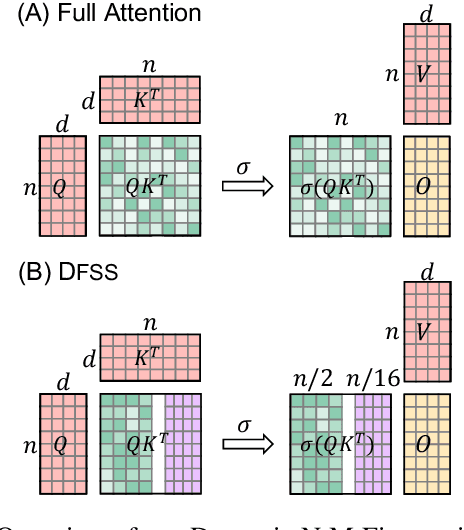
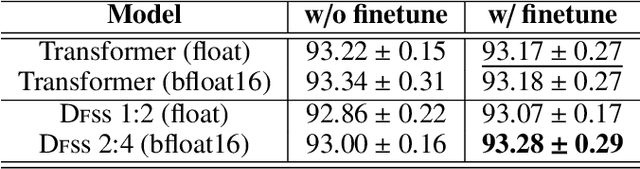
Transformers are becoming the mainstream solutions for various tasks like NLP and Computer vision. Despite their success, the high complexity of the attention mechanism hinders them from being applied to latency-sensitive tasks. Tremendous efforts have been made to alleviate this problem, and many of them successfully reduce the asymptotic complexity to linear. Nevertheless, most of them fail to achieve practical speedup over the original full attention under moderate sequence lengths and are unfriendly to finetuning. In this paper, we present DFSS, an attention mechanism that dynamically prunes the full attention weight matrix to N:M fine-grained structured sparse pattern. We provide both theoretical and empirical evidence that demonstrates DFSS is a good approximation of the full attention mechanism. We propose a dedicated CUDA kernel design that completely eliminates the dynamic pruning overhead and achieves speedups under arbitrary sequence length. We evaluate the 1:2 and 2:4 sparsity under different configurations and achieve 1.27~ 1.89x speedups over the full-attention mechanism. It only takes a couple of finetuning epochs from the pretrained model to achieve on par accuracy with full attention mechanism on tasks from various domains under different sequence lengths from 384 to 4096.

Transformer Acceleration with Dynamic Sparse Attention

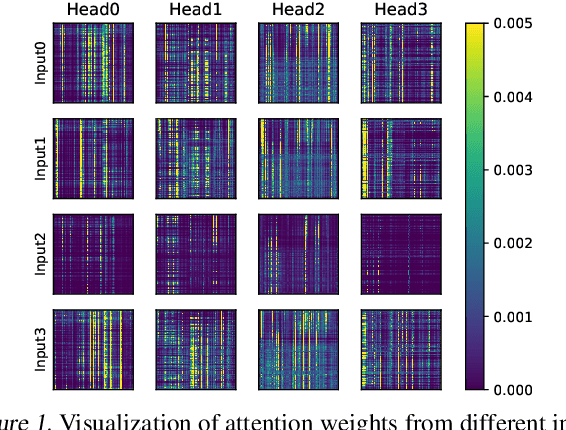
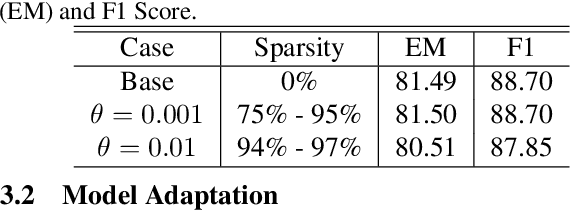
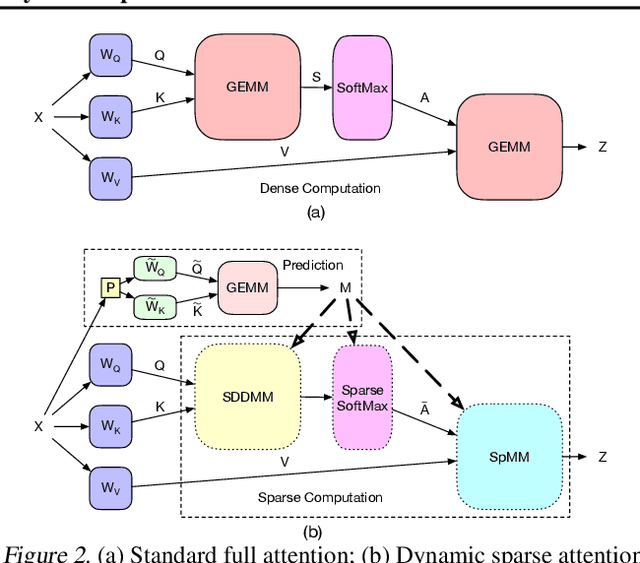
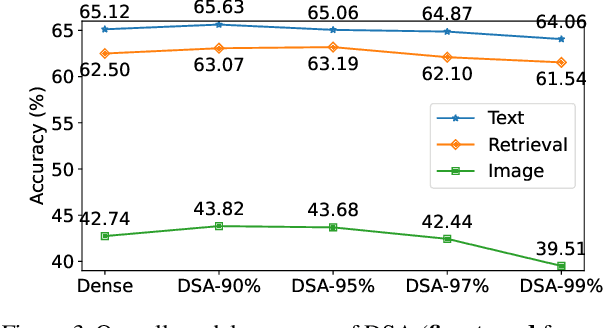
Transformers are the mainstream of NLP applications and are becoming increasingly popular in other domains such as Computer Vision. Despite the improvements in model quality, the enormous computation costs make Transformers difficult at deployment, especially when the sequence length is large in emerging applications. Processing attention mechanism as the essential component of Transformer is the bottleneck of execution due to the quadratic complexity. Prior art explores sparse patterns in attention to support long sequence modeling, but those pieces of work are on static or fixed patterns. We demonstrate that the sparse patterns are dynamic, depending on input sequences. Thus, we propose the Dynamic Sparse Attention (DSA) that can efficiently exploit the dynamic sparsity in the attention of Transformers. Compared with other methods, our approach can achieve better trade-offs between accuracy and model complexity. Moving forward, we identify challenges and provide solutions to implement DSA on existing hardware (GPUs) and specialized hardware in order to achieve practical speedup and efficiency improvements for Transformer execution.

H2Learn: High-Efficiency Learning Accelerator for High-Accuracy Spiking Neural Networks

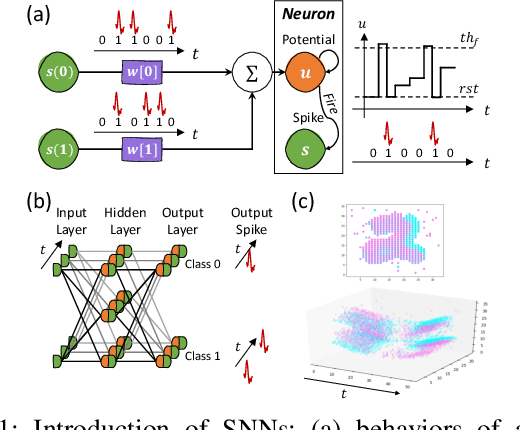
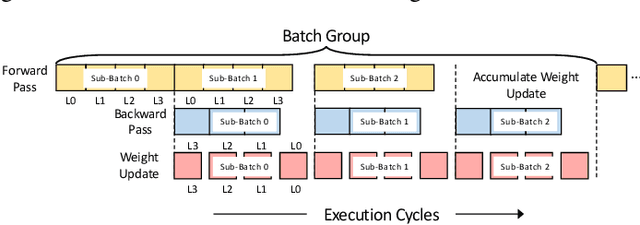
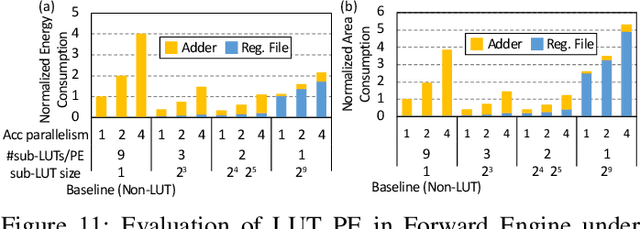
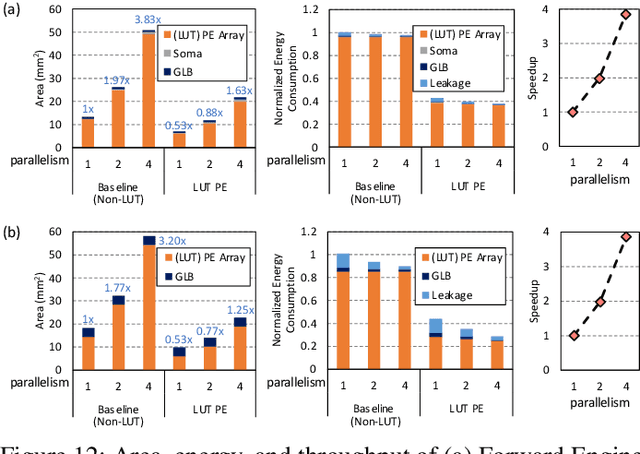
Although spiking neural networks (SNNs) take benefits from the bio-plausible neural modeling, the low accuracy under the common local synaptic plasticity learning rules limits their application in many practical tasks. Recently, an emerging SNN supervised learning algorithm inspired by backpropagation through time (BPTT) from the domain of artificial neural networks (ANNs) has successfully boosted the accuracy of SNNs and helped improve the practicability of SNNs. However, current general-purpose processors suffer from low efficiency when performing BPTT for SNNs due to the ANN-tailored optimization. On the other hand, current neuromorphic chips cannot support BPTT because they mainly adopt local synaptic plasticity rules for simplified implementation. In this work, we propose H2Learn, a novel architecture that can achieve high efficiency for BPTT-based SNN learning which ensures high accuracy of SNNs. At the beginning, we characterized the behaviors of BPTT-based SNN learning. Benefited from the binary spike-based computation in the forward pass and the weight update, we first design lookup table (LUT) based processing elements in Forward Engine and Weight Update Engine to make accumulations implicit and to fuse the computations of multiple input points. Second, benefited from the rich sparsity in the backward pass, we design a dual-sparsity-aware Backward Engine which exploits both input and output sparsity. Finally, we apply a pipeline optimization between different engines to build an end-to-end solution for the BPTT-based SNN learning. Compared with the modern NVIDIA V100 GPU, H2Learn achieves 7.38x area saving, 5.74-10.20x speedup, and 5.25-7.12x energy saving on several benchmark datasets.

SAGA with Arbitrary Sampling

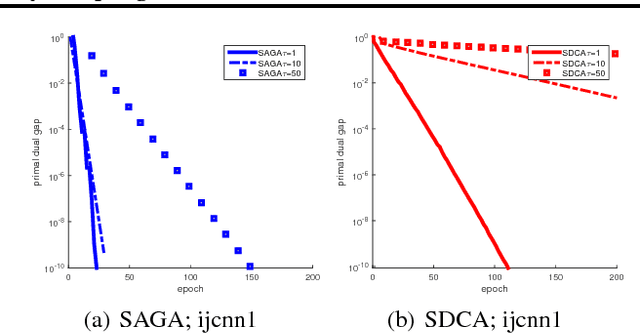
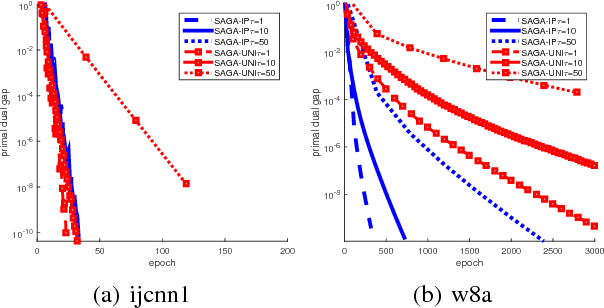
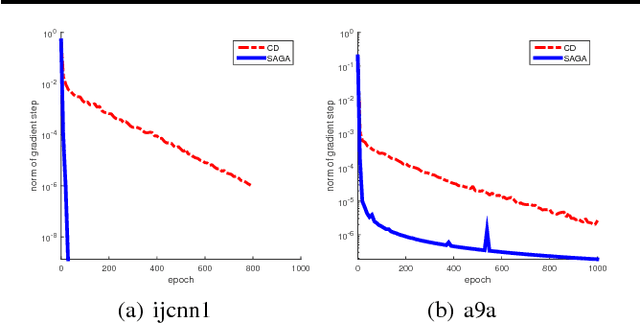
We study the problem of minimizing the average of a very large number of smooth functions, which is of key importance in training supervised learning models. One of the most celebrated methods in this context is the SAGA algorithm. Despite years of research on the topic, a general-purpose version of SAGA---one that would include arbitrary importance sampling and minibatching schemes---does not exist. We remedy this situation and propose a general and flexible variant of SAGA following the {\em arbitrary sampling} paradigm. We perform an iteration complexity analysis of the method, largely possible due to the construction of new stochastic Lyapunov functions. We establish linear convergence rates in the smooth and strongly convex regime, and under a quadratic functional growth condition (i.e., in a regime not assuming strong convexity). Our rates match those of the primal-dual method Quartz for which an arbitrary sampling analysis is available, which makes a significant step towards closing the gap in our understanding of complexity of primal and dual methods for finite sum problems.

Even Faster Accelerated Coordinate Descent Using Non-Uniform Sampling

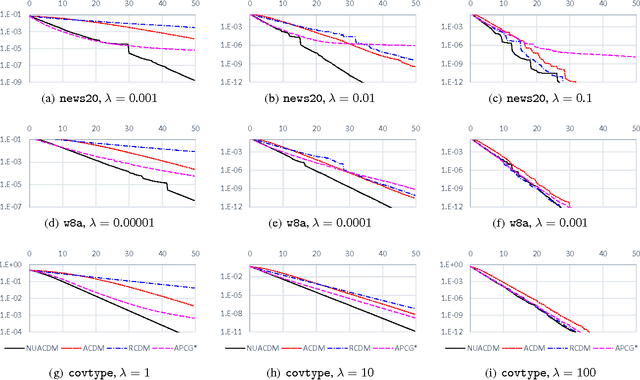
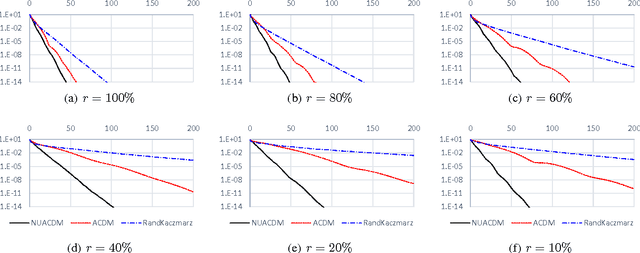
Accelerated coordinate descent is widely used in optimization due to its cheap per-iteration cost and scalability to large-scale problems. Up to a primal-dual transformation, it is also the same as accelerated stochastic gradient descent that is one of the central methods used in machine learning. In this paper, we improve the best known running time of accelerated coordinate descent by a factor up to $\sqrt{n}$. Our improvement is based on a clean, novel non-uniform sampling that selects each coordinate with a probability proportional to the square root of its smoothness parameter. Our proof technique also deviates from the classical estimation sequence technique used in prior work. Our speed-up applies to important problems such as empirical risk minimization and solving linear systems, both in theory and in practice.

Coordinate Descent with Arbitrary Sampling I: Algorithms and Complexity

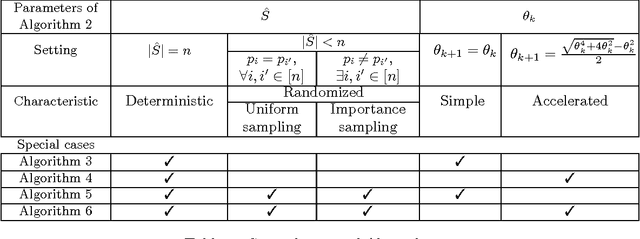
We study the problem of minimizing the sum of a smooth convex function and a convex block-separable regularizer and propose a new randomized coordinate descent method, which we call ALPHA. Our method at every iteration updates a random subset of coordinates, following an arbitrary distribution. No coordinate descent methods capable to handle an arbitrary sampling have been studied in the literature before for this problem. ALPHA is a remarkably flexible algorithm: in special cases, it reduces to deterministic and randomized methods such as gradient descent, coordinate descent, parallel coordinate descent and distributed coordinate descent -- both in nonaccelerated and accelerated variants. The variants with arbitrary (or importance) sampling are new. We provide a complexity analysis of ALPHA, from which we deduce as a direct corollary complexity bounds for its many variants, all matching or improving best known bounds.

Coordinate Descent with Arbitrary Sampling II: Expected Separable Overapproximation

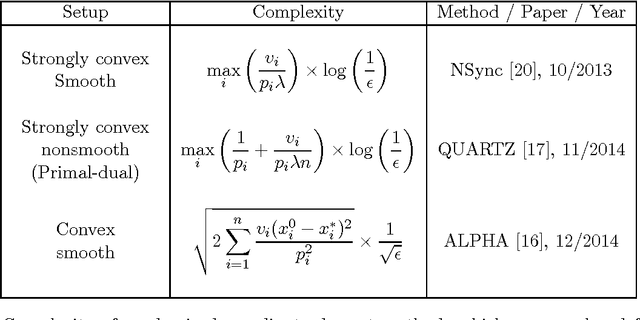
The design and complexity analysis of randomized coordinate descent methods, and in particular of variants which update a random subset (sampling) of coordinates in each iteration, depends on the notion of expected separable overapproximation (ESO). This refers to an inequality involving the objective function and the sampling, capturing in a compact way certain smoothness properties of the function in a random subspace spanned by the sampled coordinates. ESO inequalities were previously established for special classes of samplings only, almost invariably for uniform samplings. In this paper we develop a systematic technique for deriving these inequalities for a large class of functions and for arbitrary samplings. We demonstrate that one can recover existing ESO results using our general approach, which is based on the study of eigenvalues associated with samplings and the data describing the function.

Stochastic Dual Coordinate Ascent with Adaptive Probabilities

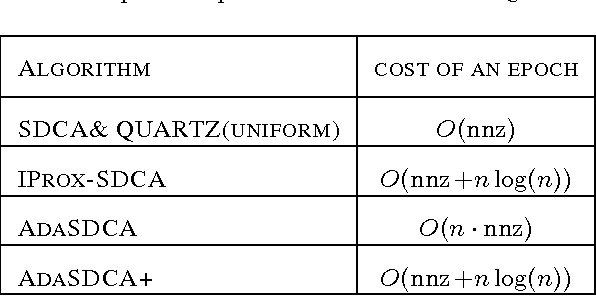
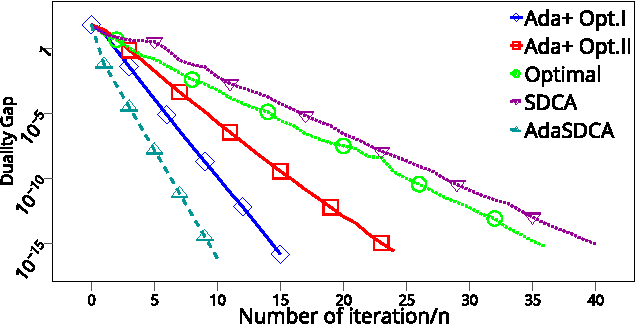
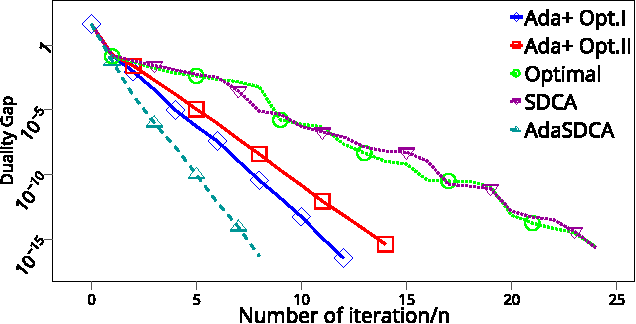
This paper introduces AdaSDCA: an adaptive variant of stochastic dual coordinate ascent (SDCA) for solving the regularized empirical risk minimization problems. Our modification consists in allowing the method adaptively change the probability distribution over the dual variables throughout the iterative process. AdaSDCA achieves provably better complexity bound than SDCA with the best fixed probability distribution, known as importance sampling. However, it is of a theoretical character as it is expensive to implement. We also propose AdaSDCA+: a practical variant which in our experiments outperforms existing non-adaptive methods.

SDNA: Stochastic Dual Newton Ascent for Empirical Risk Minimization

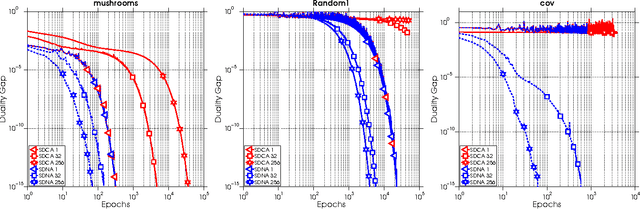
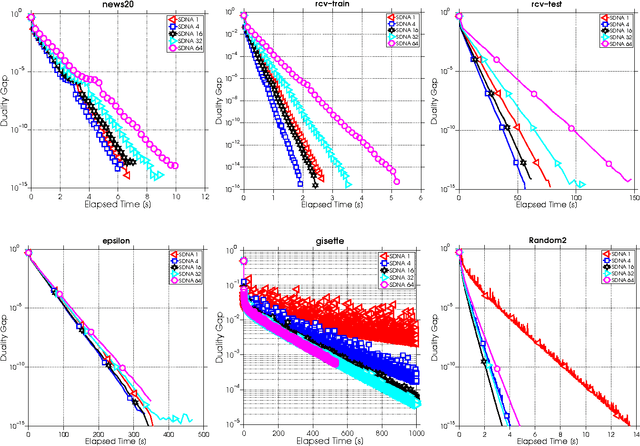
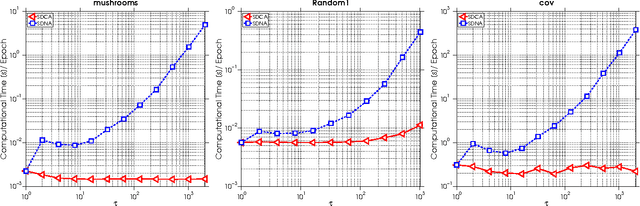
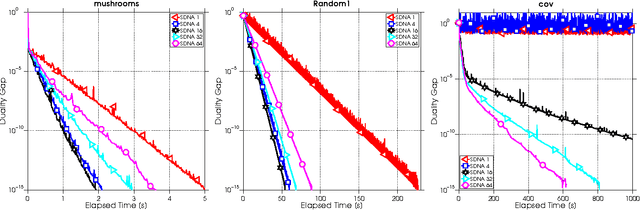
We propose a new algorithm for minimizing regularized empirical loss: Stochastic Dual Newton Ascent (SDNA). Our method is dual in nature: in each iteration we update a random subset of the dual variables. However, unlike existing methods such as stochastic dual coordinate ascent, SDNA is capable of utilizing all curvature information contained in the examples, which leads to striking improvements in both theory and practice - sometimes by orders of magnitude. In the special case when an L2-regularizer is used in the primal, the dual problem is a concave quadratic maximization problem plus a separable term. In this regime, SDNA in each step solves a proximal subproblem involving a random principal submatrix of the Hessian of the quadratic function; whence the name of the method. If, in addition, the loss functions are quadratic, our method can be interpreted as a novel variant of the recently introduced Iterative Hessian Sketch.

Randomized Dual Coordinate Ascent with Arbitrary Sampling

We study the problem of minimizing the average of a large number of smooth convex functions penalized with a strongly convex regularizer. We propose and analyze a novel primal-dual method (Quartz) which at every iteration samples and updates a random subset of the dual variables, chosen according to an arbitrary distribution. In contrast to typical analysis, we directly bound the decrease of the primal-dual error (in expectation), without the need to first analyze the dual error. Depending on the choice of the sampling, we obtain efficient serial, parallel and distributed variants of the method. In the serial case, our bounds match the best known bounds for SDCA (both with uniform and importance sampling). With standard mini-batching, our bounds predict initial data-independent speedup as well as additional data-driven speedup which depends on spectral and sparsity properties of the data. We calculate theoretical speedup factors and find that they are excellent predictors of actual speedup in practice. Moreover, we illustrate that it is possible to design an efficient mini-batch importance sampling. The distributed variant of Quartz is the first distributed SDCA-like method with an analysis for non-separable data.