SAGA with Arbitrary Sampling
Paper and Code
Jan 24, 2019
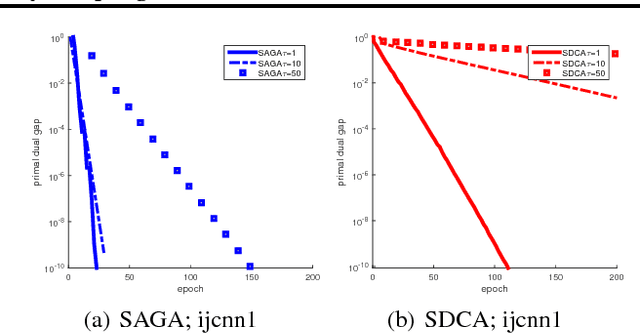
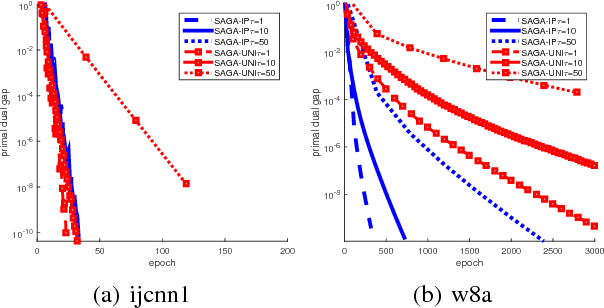
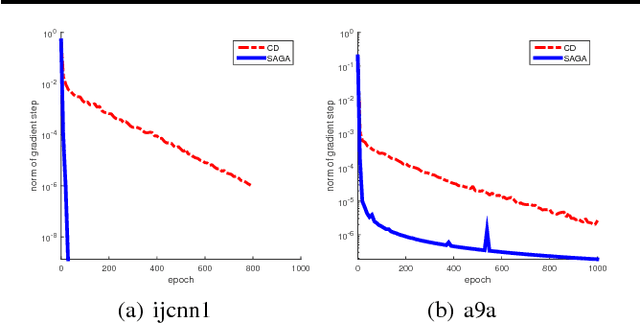
We study the problem of minimizing the average of a very large number of smooth functions, which is of key importance in training supervised learning models. One of the most celebrated methods in this context is the SAGA algorithm. Despite years of research on the topic, a general-purpose version of SAGA---one that would include arbitrary importance sampling and minibatching schemes---does not exist. We remedy this situation and propose a general and flexible variant of SAGA following the {\em arbitrary sampling} paradigm. We perform an iteration complexity analysis of the method, largely possible due to the construction of new stochastic Lyapunov functions. We establish linear convergence rates in the smooth and strongly convex regime, and under a quadratic functional growth condition (i.e., in a regime not assuming strong convexity). Our rates match those of the primal-dual method Quartz for which an arbitrary sampling analysis is available, which makes a significant step towards closing the gap in our understanding of complexity of primal and dual methods for finite sum problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge