Xu Qian
Channel-wise Hessian Aware trace-Weighted Quantization of Neural Networks
Aug 19, 2020
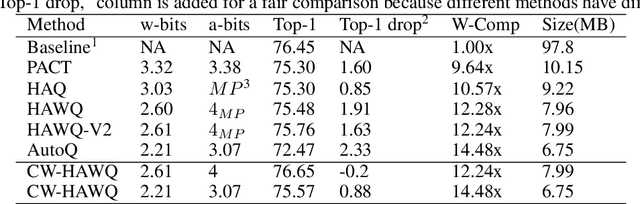
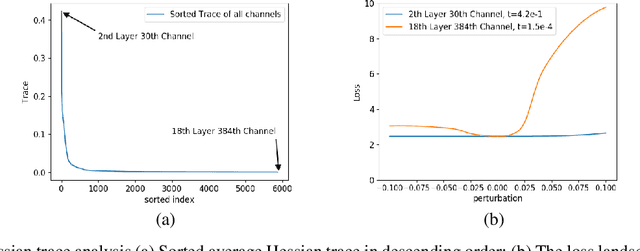
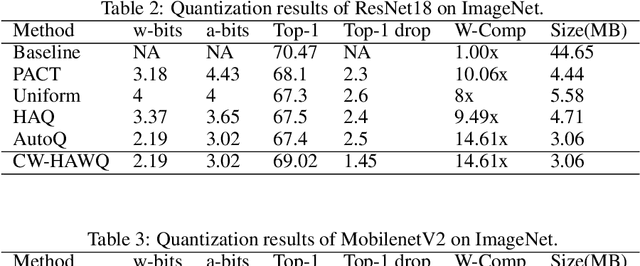
Abstract:Second-order information has proven to be very effective in determining the redundancy of neural network weights and activations. Recent paper proposes to use Hessian traces of weights and activations for mixed-precision quantization and achieves state-of-the-art results. However, prior works only focus on selecting bits for each layer while the redundancy of different channels within a layer also differ a lot. This is mainly because the complexity of determining bits for each channel is too high for original methods. Here, we introduce Channel-wise Hessian Aware trace-Weighted Quantization (CW-HAWQ). CW-HAWQ uses Hessian trace to determine the relative sensitivity order of different channels of activations and weights. What's more, CW-HAWQ proposes to use deep Reinforcement learning (DRL) Deep Deterministic Policy Gradient (DDPG)-based agent to find the optimal ratios of different quantization bits and assign bits to channels according to the Hessian trace order. The number of states in CW-HAWQ is much smaller compared with traditional AutoML based mix-precision methods since we only need to search ratios for the quantization bits. Compare CW-HAWQ with state-of-the-art shows that we can achieve better results for multiple networks.
SAGA with Arbitrary Sampling
Jan 24, 2019
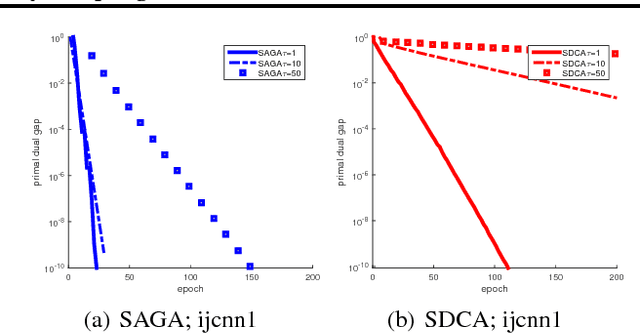
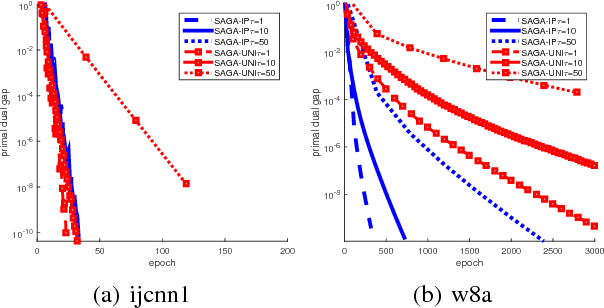
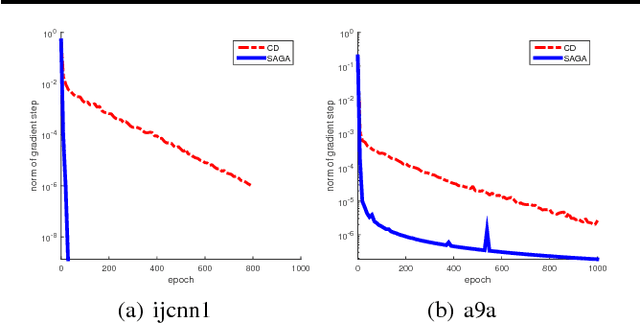
Abstract:We study the problem of minimizing the average of a very large number of smooth functions, which is of key importance in training supervised learning models. One of the most celebrated methods in this context is the SAGA algorithm. Despite years of research on the topic, a general-purpose version of SAGA---one that would include arbitrary importance sampling and minibatching schemes---does not exist. We remedy this situation and propose a general and flexible variant of SAGA following the {\em arbitrary sampling} paradigm. We perform an iteration complexity analysis of the method, largely possible due to the construction of new stochastic Lyapunov functions. We establish linear convergence rates in the smooth and strongly convex regime, and under a quadratic functional growth condition (i.e., in a regime not assuming strong convexity). Our rates match those of the primal-dual method Quartz for which an arbitrary sampling analysis is available, which makes a significant step towards closing the gap in our understanding of complexity of primal and dual methods for finite sum problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge