Using Random Codebooks for Audio Neural AutoEncoders

Latent representation learning has been an active field of study for decades in numerous applications. Inspired among others by the tokenization from Natural Language Processing and motivated by the research of a simple data representation, recent works have introduced a quantization step into the feature extraction. In this work, we propose a novel strategy to build the neural discrete representation by means of random codebooks. These codebooks are obtained by randomly sampling a large, predefined fixed codebook. We experimentally show the merits and potential of our approach in a task of audio compression and reconstruction.

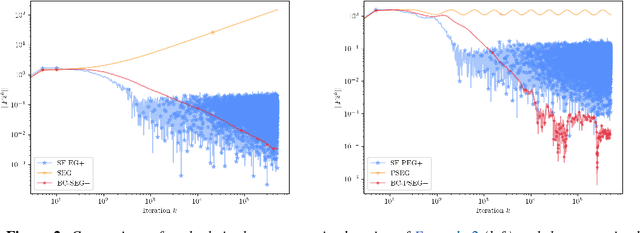
Escaping limit cycles: Global convergence for constrained nonconvex-nonconcave minimax problems

This paper introduces a new extragradient-type algorithm for a class of nonconvex-nonconcave minimax problems. It is well-known that finding a local solution for general minimax problems is computationally intractable. This observation has recently motivated the study of structures sufficient for convergence of first order methods in the more general setting of variational inequalities when the so-called weak Minty variational inequality (MVI) holds. This problem class captures non-trivial structures as we demonstrate with examples, for which a large family of existing algorithms provably converge to limit cycles. Our results require a less restrictive parameter range in the weak MVI compared to what is previously known, thus extending the applicability of our scheme. The proposed algorithm is applicable to constrained and regularized problems, and involves an adaptive stepsize allowing for potentially larger stepsizes. Our scheme also converges globally even in settings where the underlying operator exhibits limit cycles.

Solving stochastic weak Minty variational inequalities without increasing batch size

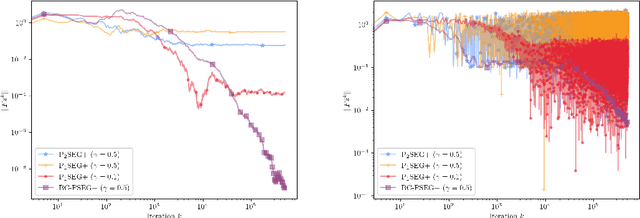
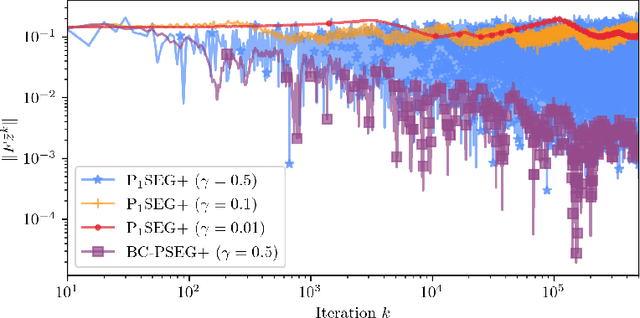
This paper introduces a family of stochastic extragradient-type algorithms for a class of nonconvex-nonconcave problems characterized by the weak Minty variational inequality (MVI). Unlike existing results on extragradient methods in the monotone setting, employing diminishing stepsizes is no longer possible in the weak MVI setting. This has led to approaches such as increasing batch sizes per iteration which can however be prohibitively expensive. In contrast, our proposed methods involves two stepsizes and only requires one additional oracle evaluation per iteration. We show that it is possible to keep one fixed stepsize while it is only the second stepsize that is taken to be diminishing, making it interesting even in the monotone setting. Almost sure convergence is established and we provide a unified analysis for this family of schemes which contains a nonlinear generalization of the celebrated primal dual hybrid gradient algorithm.

Screening Rules and its Complexity for Active Set Identification

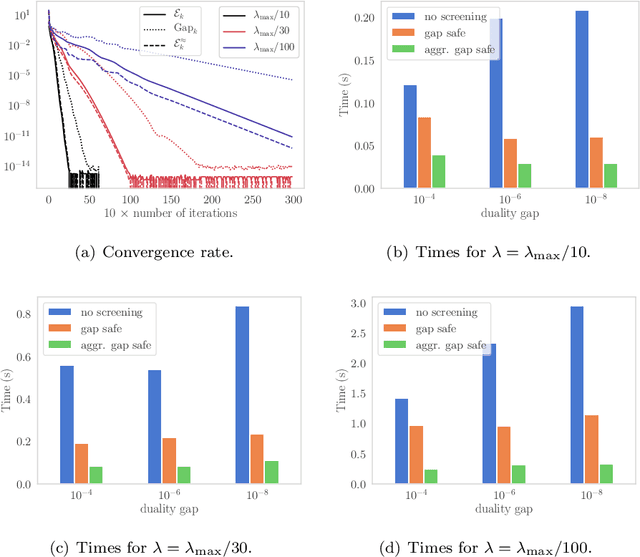
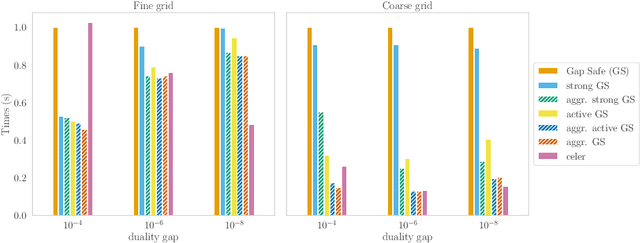
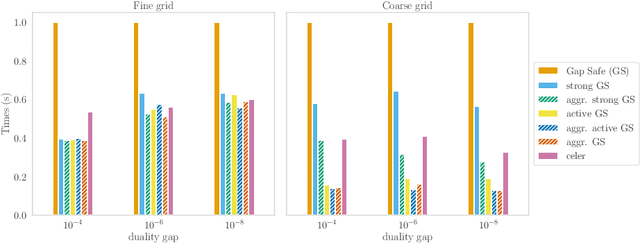
Screening rules were recently introduced as a technique for explicitly identifying active structures such as sparsity, in optimization problem arising in machine learning. This has led to new methods of acceleration based on a substantial dimension reduction. We show that screening rules stem from a combination of natural properties of subdifferential sets and optimality conditions, and can hence be understood in a unified way. Under mild assumptions, we analyze the number of iterations needed to identify the optimal active set for any converging algorithm. We show that it only depends on its convergence rate.

Random extrapolation for primal-dual coordinate descent

We introduce a randomly extrapolated primal-dual coordinate descent method that adapts to sparsity of the data matrix and the favorable structures of the objective function. Our method updates only a subset of primal and dual variables with sparse data, and it uses large step sizes with dense data, retaining the benefits of the specific methods designed for each case. In addition to adapting to sparsity, our method attains fast convergence guarantees in favorable cases \textit{without any modifications}. In particular, we prove linear convergence under metric subregularity, which applies to strongly convex-strongly concave problems and piecewise linear quadratic functions. We show almost sure convergence of the sequence and optimal sublinear convergence rates for the primal-dual gap and objective values, in the general convex-concave case. Numerical evidence demonstrates the state-of-the-art empirical performance of our method in sparse and dense settings, matching and improving the existing methods.

Improved Optimistic Algorithms for Logistic Bandits

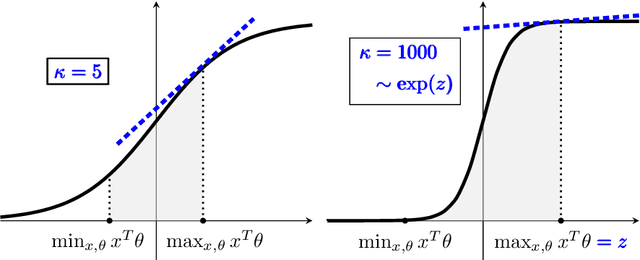
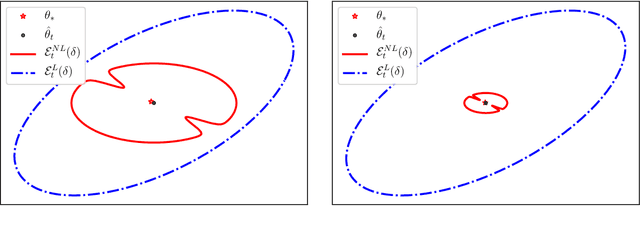
The generalized linear bandit framework has attracted a lot of attention in recent years by extending the well-understood linear setting and allowing to model richer reward structures. It notably covers the logistic model, widely used when rewards are binary. For logistic bandits, the frequentist regret guarantees of existing algorithms are $\tilde{\mathcal{O}}(\kappa \sqrt{T})$, where $\kappa$ is a problem-dependent constant. Unfortunately, $\kappa$ can be arbitrarily large as it scales exponentially with the size of the decision set. This may lead to significantly loose regret bounds and poor empirical performance. In this work, we study the logistic bandit with a focus on the prohibitive dependencies introduced by $\kappa$. We propose a new optimistic algorithm based on a finer examination of the non-linearities of the reward function. We show that it enjoys a $\tilde{\mathcal{O}}(\sqrt{T})$ regret with no dependency in $\kappa$, but for a second order term. Our analysis is based on a new tail-inequality for self-normalized martingales, of independent interest.

Improving Evolutionary Strategies with Generative Neural Networks

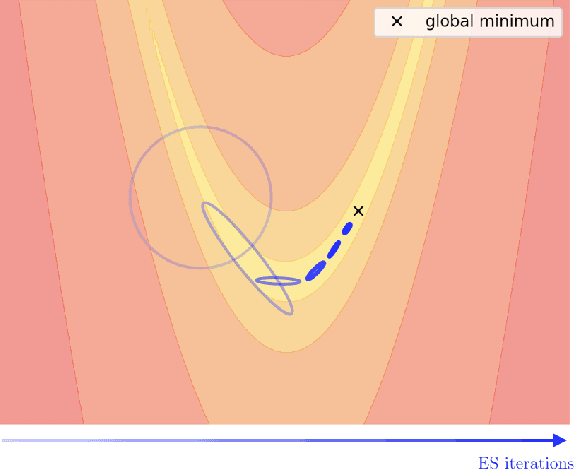
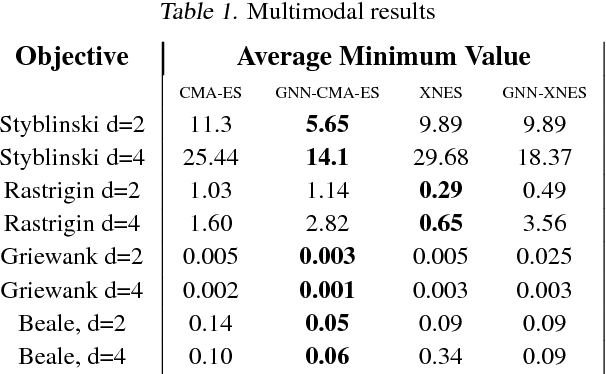
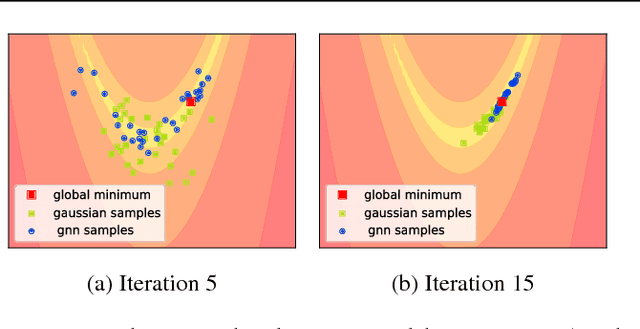
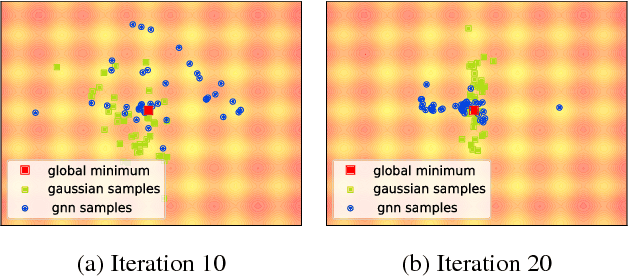
Evolutionary Strategies (ES) are a popular family of black-box zeroth-order optimization algorithms which rely on search distributions to efficiently optimize a large variety of objective functions. This paper investigates the potential benefits of using highly flexible search distributions in classical ES algorithms, in contrast to standard ones (typically Gaussians). We model such distributions with Generative Neural Networks (GNNs) and introduce a new training algorithm that leverages their expressiveness to accelerate the ES procedure. We show that this tailored algorithm can readily incorporate existing ES algorithms, and outperforms the state-of-the-art on diverse objective functions.

Stochastic Conditional Gradient Method for Composite Convex Minimization

In this paper, we propose the first practical algorithm to minimize stochastic composite optimization problems over compact convex sets. This template allows for affine constraints and therefore covers stochastic semidefinite programs (SDPs), which are vastly applicable in both machine learning and statistics. In this setup, stochastic algorithms with convergence guarantees are either not known or not tractable. We tackle this general problem and propose a convergent, easy to implement and tractable algorithm. We prove $\mathcal{O}(k^{-1/3})$ convergence rate in expectation on the objective residual and $\mathcal{O}(k^{-5/12})$ in expectation on the feasibility gap. These rates are achieved without increasing the batchsize, which can contain a single sample. We present extensive empirical evidence demonstrating the superiority of our algorithm on a broad range of applications including optimization of stochastic SDPs.

Safe Grid Search with Optimal Complexity

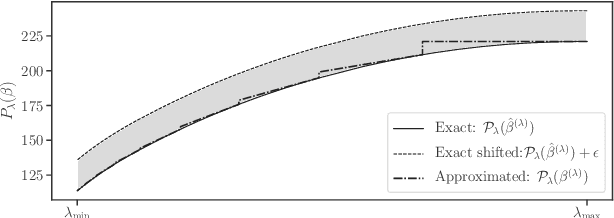
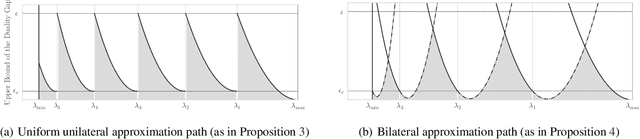
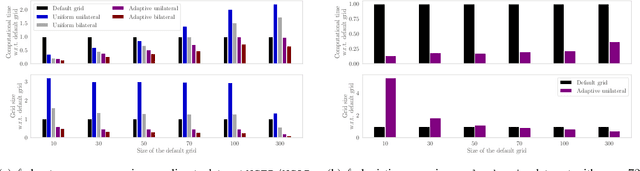
Popular machine learning estimators involve regularization parameters that can be challenging to tune, and standard strategies rely on grid search for this task. In this paper, we revisit the techniques of approximating the regularization path up to predefined tolerance $\epsilon$ in a unified framework and show that its complexity is $O(1/\sqrt[d]{\epsilon})$ for uniformly convex loss of order $d>0$ and $O(1/\sqrt{\epsilon})$ for Generalized Self-Concordant functions. This framework encompasses least-squares but also logistic regression (a case that as far as we know was not handled as precisely by previous works). We leverage our technique to provide refined bounds on the validation error as well as a practical algorithm for hyperparameter tuning. The later has global convergence guarantee when targeting a prescribed accuracy on the validation set. Last but not least, our approach helps relieving the practitioner from the (often neglected) task of selecting a stopping criterion when optimizing over the training set: our method automatically calibrates it based on the targeted accuracy on the validation set.

Neural Generative Models for Global Optimization with Gradients

The aim of global optimization is to find the global optimum of arbitrary classes of functions, possibly highly multimodal ones. In this paper we focus on the subproblem of global optimization for differentiable functions and we propose an Evolutionary Search-inspired solution where we model point search distributions via Generative Neural Networks. This approach enables us to model diverse and complex search distributions based on which we can efficiently explore complicated objective landscapes. In our experiments we show the practical superiority of our algorithm versus classical Evolutionary Search and gradient-based solutions on a benchmark set of multimodal functions, and demonstrate how it can be used to accelerate Bayesian Optimization with Gaussian Processes.