Spingarn's Method and Progressive Decoupling Beyond Elicitable Monotonicity

Spingarn's method of partial inverses and the progressive decoupling algorithm address inclusion problems involving the sum of an operator and the normal cone of a linear subspace, known as linkage problems. Despite their success, existing convergence results are limited to the so-called elicitable monotone setting, where nonmonotonicity is allowed only on the orthogonal complement of the linkage subspace. In this paper, we introduce progressive decoupling+, a generalized version of standard progressive decoupling that incorporates separate relaxation parameters for the linkage subspace and its orthogonal complement. We prove convergence under conditions that link the relaxation parameters to the nonmonotonicity of their respective subspaces and show that the special cases of Spingarn's method and standard progressive decoupling also extend beyond the elicitable monotone setting. Our analysis hinges upon an equivalence between progressive decoupling+ and the preconditioned proximal point algorithm, for which we develop a general local convergence analysis in a certain nonmonotone setting.

Adaptive proximal gradient methods are universal without approximation

We show that adaptive proximal gradient methods for convex problems are not restricted to traditional Lipschitzian assumptions. Our analysis reveals that a class of linesearch-free methods is still convergent under mere local H\"older gradient continuity, covering in particular continuously differentiable semi-algebraic functions. To mitigate the lack of local Lipschitz continuity, popular approaches revolve around $\varepsilon$-oracles and/or linesearch procedures. In contrast, we exploit plain H\"older inequalities not entailing any approximation, all while retaining the linesearch-free nature of adaptive schemes. Furthermore, we prove full sequence convergence without prior knowledge of local H\"older constants nor of the order of H\"older continuity. In numerical experiments we present comparisons to baseline methods on diverse tasks from machine learning covering both the locally and the globally H\"older setting.

Convergence of the Chambolle-Pock Algorithm in the Absence of Monotonicity

The Chambolle-Pock algorithm (CPA), also known as the primal-dual hybrid gradient method (PDHG), has surged in popularity in the last decade due to its success in solving convex/monotone structured problems. This work provides convergence results for problems with varying degrees of (non)monotonicity, quantified through a so-called oblique weak Minty condition on the associated primal-dual operator. Our results reveal novel stepsize and relaxation parameter ranges which do not only depend on the norm of the linear mapping, but also on its other singular values. In particular, in nonmonotone settings, in addition to the classical stepsize conditions for CPA, extra bounds on the stepsizes and relaxation parameters are required. On the other hand, in the strongly monotone setting, the relaxation parameter is allowed to exceed the classical upper bound of two. Moreover, sufficient convergence conditions are obtained when the individual operators belong to the recently introduced class of semimonotone operators. Since this class of operators encompasses many traditional operator classes including (hypo)- and co(hypo)monotone operators, this analysis recovers and extends existing results for CPA. Several examples are provided for the aforementioned problem classes to demonstrate and establish tightness of the proposed stepsize ranges.

On the convergence of adaptive first order methods: proximal gradient and alternating minimization algorithms

Building upon recent works on linesearch-free adaptive proximal gradient methods, this paper proposes AdaPG$^{\pi,r}$, a framework that unifies and extends existing results by providing larger stepsize policies and improved lower bounds. Different choices of the parameters $\pi$ and $r$ are discussed and the efficacy of the resulting methods is demonstrated through numerical simulations. In an attempt to better understand the underlying theory, its convergence is established in a more general setting that allows for time-varying parameters. Finally, an adaptive alternating minimization algorithm is presented by exploring the dual setting. This algorithm not only incorporates additional adaptivity, but also expands its applicability beyond standard strongly convex settings.

Escaping limit cycles: Global convergence for constrained nonconvex-nonconcave minimax problems

This paper introduces a new extragradient-type algorithm for a class of nonconvex-nonconcave minimax problems. It is well-known that finding a local solution for general minimax problems is computationally intractable. This observation has recently motivated the study of structures sufficient for convergence of first order methods in the more general setting of variational inequalities when the so-called weak Minty variational inequality (MVI) holds. This problem class captures non-trivial structures as we demonstrate with examples, for which a large family of existing algorithms provably converge to limit cycles. Our results require a less restrictive parameter range in the weak MVI compared to what is previously known, thus extending the applicability of our scheme. The proposed algorithm is applicable to constrained and regularized problems, and involves an adaptive stepsize allowing for potentially larger stepsizes. Our scheme also converges globally even in settings where the underlying operator exhibits limit cycles.

Solving stochastic weak Minty variational inequalities without increasing batch size

This paper introduces a family of stochastic extragradient-type algorithms for a class of nonconvex-nonconcave problems characterized by the weak Minty variational inequality (MVI). Unlike existing results on extragradient methods in the monotone setting, employing diminishing stepsizes is no longer possible in the weak MVI setting. This has led to approaches such as increasing batch sizes per iteration which can however be prohibitively expensive. In contrast, our proposed methods involves two stepsizes and only requires one additional oracle evaluation per iteration. We show that it is possible to keep one fixed stepsize while it is only the second stepsize that is taken to be diminishing, making it interesting even in the monotone setting. Almost sure convergence is established and we provide a unified analysis for this family of schemes which contains a nonlinear generalization of the celebrated primal dual hybrid gradient algorithm.

SPIRAL: A Superlinearly Convergent Incremental Proximal Algorithm for Nonconvex Finite Sum Minimization

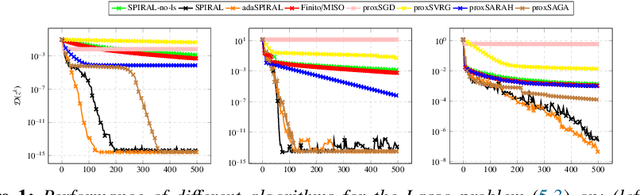
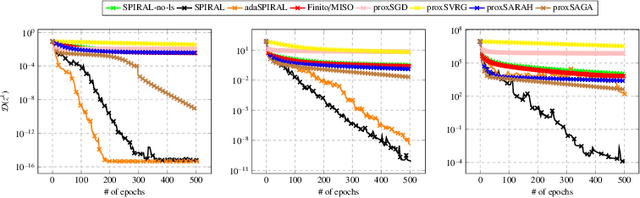
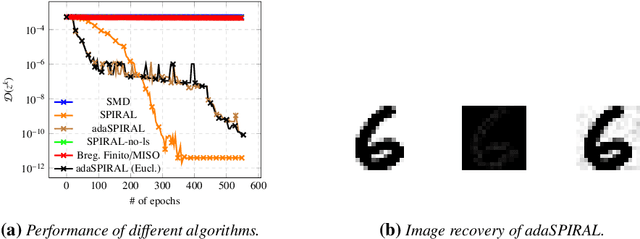
We introduce SPIRAL, a SuPerlinearly convergent Incremental pRoximal ALgorithm, for solving nonconvex regularized finite sum problems under a relative smoothness assumption. In the spirit of SVRG and SARAH, each iteration of SPIRAL consists of an inner and an outer loop. It combines incremental and full (proximal) gradient updates with a linesearch. It is shown that when using quasi-Newton directions, superlinear convergence is attained under mild assumptions at the limit points. More importantly, thanks to said linesearch, global convergence is ensured while it is shown that unit stepsize will be eventually always accepted. Simulation results on different convex, nonconvex, and non-Lipschitz differentiable problems show that our algorithm as well as its adaptive variant are competitive to the state of the art.