SAMPa: Sharpness-aware Minimization Parallelized

Sharpness-aware minimization (SAM) has been shown to improve the generalization of neural networks. However, each SAM update requires \emph{sequentially} computing two gradients, effectively doubling the per-iteration cost compared to base optimizers like SGD. We propose a simple modification of SAM, termed SAMPa, which allows us to fully parallelize the two gradient computations. SAMPa achieves a twofold speedup of SAM under the assumption that communication costs between devices are negligible. Empirical results show that SAMPa ranks among the most efficient variants of SAM in terms of computational time. Additionally, our method consistently outperforms SAM across both vision and language tasks. Notably, SAMPa theoretically maintains convergence guarantees even for \emph{fixed} perturbation sizes, which is established through a novel Lyapunov function. We in fact arrive at SAMPa by treating this convergence guarantee as a hard requirement -- an approach we believe is promising for developing SAM-based methods in general. Our code is available at \url{https://github.com/LIONS-EPFL/SAMPa}.

Improving SAM Requires Rethinking its Optimization Formulation

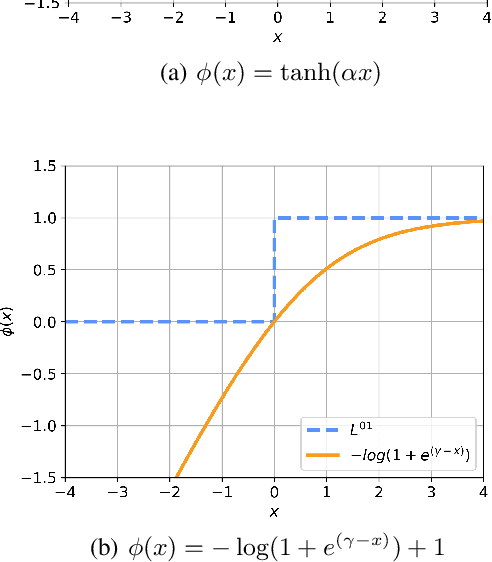
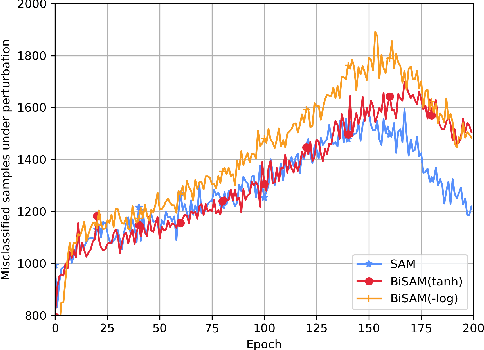
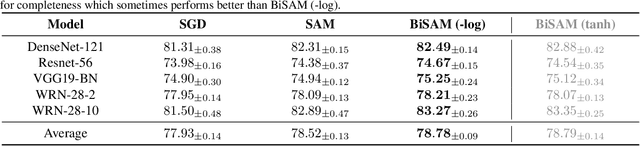
This paper rethinks Sharpness-Aware Minimization (SAM), which is originally formulated as a zero-sum game where the weights of a network and a bounded perturbation try to minimize/maximize, respectively, the same differentiable loss. To fundamentally improve this design, we argue that SAM should instead be reformulated using the 0-1 loss. As a continuous relaxation, we follow the simple conventional approach where the minimizing (maximizing) player uses an upper bound (lower bound) surrogate to the 0-1 loss. This leads to a novel formulation of SAM as a bilevel optimization problem, dubbed as BiSAM. BiSAM with newly designed lower-bound surrogate loss indeed constructs stronger perturbation. Through numerical evidence, we show that BiSAM consistently results in improved performance when compared to the original SAM and variants, while enjoying similar computational complexity. Our code is available at https://github.com/LIONS-EPFL/BiSAM.

Stable Nonconvex-Nonconcave Training via Linear Interpolation

This paper presents a theoretical analysis of linear interpolation as a principled method for stabilizing (large-scale) neural network training. We argue that instabilities in the optimization process are often caused by the nonmonotonicity of the loss landscape and show how linear interpolation can help by leveraging the theory of nonexpansive operators. We construct a new optimization scheme called relaxed approximate proximal point (RAPP), which is the first explicit method to achieve last iterate convergence rates for the full range of cohypomonotone problems. The construction extends to constrained and regularized settings. By replacing the inner optimizer in RAPP we rediscover the family of Lookahead algorithms for which we establish convergence in cohypomonotone problems even when the base optimizer is taken to be gradient descent ascent. The range of cohypomonotone problems in which Lookahead converges is further expanded by exploiting that Lookahead inherits the properties of the base optimizer. We corroborate the results with experiments on generative adversarial networks which demonstrates the benefits of the linear interpolation present in both RAPP and Lookahead.

Federated Learning under Covariate Shifts with Generalization Guarantees

This paper addresses intra-client and inter-client covariate shifts in federated learning (FL) with a focus on the overall generalization performance. To handle covariate shifts, we formulate a new global model training paradigm and propose Federated Importance-Weighted Empirical Risk Minimization (FTW-ERM) along with improving density ratio matching methods without requiring perfect knowledge of the supremum over true ratios. We also propose the communication-efficient variant FITW-ERM with the same level of privacy guarantees as those of classical ERM in FL. We theoretically show that FTW-ERM achieves smaller generalization error than classical ERM under certain settings. Experimental results demonstrate the superiority of FTW-ERM over existing FL baselines in challenging imbalanced federated settings in terms of data distribution shifts across clients.

Escaping limit cycles: Global convergence for constrained nonconvex-nonconcave minimax problems

This paper introduces a new extragradient-type algorithm for a class of nonconvex-nonconcave minimax problems. It is well-known that finding a local solution for general minimax problems is computationally intractable. This observation has recently motivated the study of structures sufficient for convergence of first order methods in the more general setting of variational inequalities when the so-called weak Minty variational inequality (MVI) holds. This problem class captures non-trivial structures as we demonstrate with examples, for which a large family of existing algorithms provably converge to limit cycles. Our results require a less restrictive parameter range in the weak MVI compared to what is previously known, thus extending the applicability of our scheme. The proposed algorithm is applicable to constrained and regularized problems, and involves an adaptive stepsize allowing for potentially larger stepsizes. Our scheme also converges globally even in settings where the underlying operator exhibits limit cycles.

Solving stochastic weak Minty variational inequalities without increasing batch size

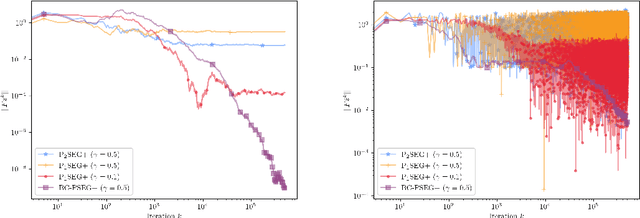
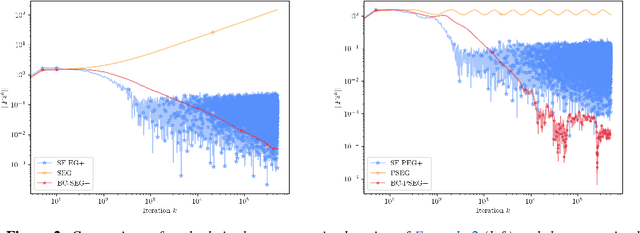
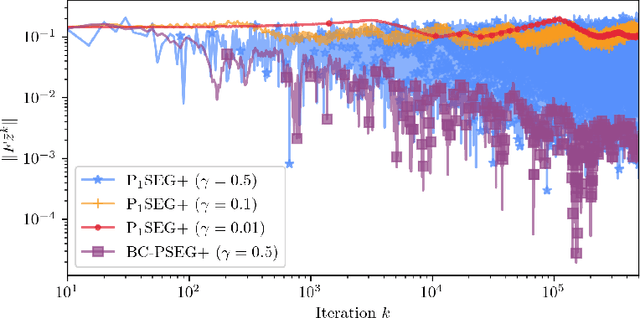
This paper introduces a family of stochastic extragradient-type algorithms for a class of nonconvex-nonconcave problems characterized by the weak Minty variational inequality (MVI). Unlike existing results on extragradient methods in the monotone setting, employing diminishing stepsizes is no longer possible in the weak MVI setting. This has led to approaches such as increasing batch sizes per iteration which can however be prohibitively expensive. In contrast, our proposed methods involves two stepsizes and only requires one additional oracle evaluation per iteration. We show that it is possible to keep one fixed stepsize while it is only the second stepsize that is taken to be diminishing, making it interesting even in the monotone setting. Almost sure convergence is established and we provide a unified analysis for this family of schemes which contains a nonlinear generalization of the celebrated primal dual hybrid gradient algorithm.

Revisiting adversarial training for the worst-performing class

Despite progress in adversarial training (AT), there is a substantial gap between the top-performing and worst-performing classes in many datasets. For example, on CIFAR10, the accuracies for the best and worst classes are 74% and 23%, respectively. We argue that this gap can be reduced by explicitly optimizing for the worst-performing class, resulting in a min-max-max optimization formulation. Our method, called class focused online learning (CFOL), includes high probability convergence guarantees for the worst class loss and can be easily integrated into existing training setups with minimal computational overhead. We demonstrate an improvement to 32% in the worst class accuracy on CIFAR10, and we observe consistent behavior across CIFAR100 and STL10. Our study highlights the importance of moving beyond average accuracy, which is particularly important in safety-critical applications.

Subquadratic Overparameterization for Shallow Neural Networks

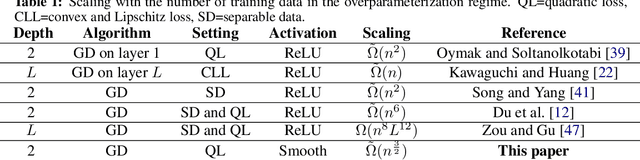
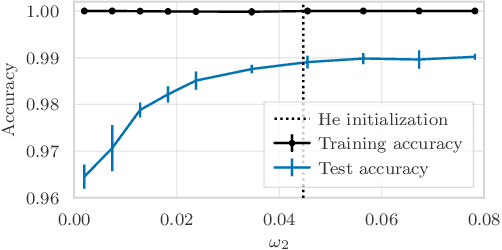
Overparameterization refers to the important phenomenon where the width of a neural network is chosen such that learning algorithms can provably attain zero loss in nonconvex training. The existing theory establishes such global convergence using various initialization strategies, training modifications, and width scalings. In particular, the state-of-the-art results require the width to scale quadratically with the number of training data under standard initialization strategies used in practice for best generalization performance. In contrast, the most recent results obtain linear scaling either with requiring initializations that lead to the "lazy-training", or training only a single layer. In this work, we provide an analytical framework that allows us to adopt standard initialization strategies, possibly avoid lazy training, and train all layers simultaneously in basic shallow neural networks while attaining a desirable subquadratic scaling on the network width. We achieve the desiderata via Polyak-Lojasiewicz condition, smoothness, and standard assumptions on data, and use tools from random matrix theory.