One-step full gradient suffices for low-rank fine-tuning, provably and efficiently

This paper studies how to improve the performance of Low-Rank Adaption (LoRA) as guided by our theoretical analysis. Our first set of theoretical results show that for random initialization and linear models, \textit{i)} LoRA will align to the certain singular subspace of one-step gradient of full fine-tuning; \textit{ii)} preconditioners improve convergence in the high-rank case. These insights motivate us to focus on preconditioned LoRA using a specific spectral initialization strategy for aligning with certain subspaces. For both linear and nonlinear models, we prove that alignment and generalization guarantees can be directly achieved at initialization, and the subsequent linear convergence can be also built. Our analysis leads to the \emph{LoRA-One} algorithm (using \emph{One}-step gradient and preconditioning), a theoretically grounded algorithm that achieves significant empirical improvement over vanilla LoRA and its variants on several benchmarks. Our theoretical analysis, based on decoupling the learning dynamics and characterizing how spectral initialization contributes to feature learning, may be of independent interest for understanding matrix sensing and deep learning theory. The source code can be found in the https://github.com/YuanheZ/LoRA-One.

Re-examining Double Descent and Scaling Laws under Norm-based Capacity via Deterministic Equivalence

We investigate double descent and scaling laws in terms of weights rather than the number of parameters. Specifically, we analyze linear and random features models using the deterministic equivalence approach from random matrix theory. We precisely characterize how the weights norm concentrate around deterministic quantities and elucidate the relationship between the expected test error and the norm-based capacity (complexity). Our results rigorously answer whether double descent exists under norm-based capacity and reshape the corresponding scaling laws. Moreover, they prompt a rethinking of the data-parameter paradigm - from under-parameterized to over-parameterized regimes - by shifting the focus to norms (weights) rather than parameter count.

Scalable Learned Model Soup on a Single GPU: An Efficient Subspace Training Strategy

Pre-training followed by fine-tuning is widely adopted among practitioners. The performance can be improved by "model soups"~\cite{wortsman2022model} via exploring various hyperparameter configurations.The Learned-Soup, a variant of model soups, significantly improves the performance but suffers from substantial memory and time costs due to the requirements of (i) having to load all fine-tuned models simultaneously, and (ii) a large computational graph encompassing all fine-tuned models. In this paper, we propose Memory Efficient Hyperplane Learned Soup (MEHL-Soup) to tackle this issue by formulating the learned soup as a hyperplane optimization problem and introducing block coordinate gradient descent to learn the mixing coefficients. At each iteration, MEHL-Soup only needs to load a few fine-tuned models and build a computational graph with one combined model. We further extend MEHL-Soup to MEHL-Soup+ in a layer-wise manner. Experimental results on various ViT models and data sets show that MEHL-Soup(+) outperforms Learned-Soup(+) in terms of test accuracy, and also reduces memory usage by more than $13\times$. Moreover, MEHL-Soup(+) can be run on a single GPU and achieves $9\times$ speed up in soup construction compared with the Learned-Soup. The code is released at https://github.com/nblt/MEHL-Soup.

Benign overfitting in Fixed Dimension via Physics-Informed Learning with Smooth Inductive Bias

Recent advances in machine learning have inspired a surge of research into reconstructing specific quantities of interest from measurements that comply with certain physical laws. These efforts focus on inverse problems that are governed by partial differential equations (PDEs). In this work, we develop an asymptotic Sobolev norm learning curve for kernel ridge(less) regression when addressing (elliptical) linear inverse problems. Our results show that the PDE operators in the inverse problem can stabilize the variance and even behave benign overfitting for fixed-dimensional problems, exhibiting different behaviors from regression problems. Besides, our investigation also demonstrates the impact of various inductive biases introduced by minimizing different Sobolev norms as a form of implicit regularization. For the regularized least squares estimator, we find that all considered inductive biases can achieve the optimal convergence rate, provided the regularization parameter is appropriately chosen. The convergence rate is actually independent to the choice of (smooth enough) inductive bias for both ridge and ridgeless regression. Surprisingly, our smoothness requirement recovered the condition found in Bayesian setting and extend the conclusion to the minimum norm interpolation estimators.

High-Dimensional Kernel Methods under Covariate Shift: Data-Dependent Implicit Regularization

This paper studies kernel ridge regression in high dimensions under covariate shifts and analyzes the role of importance re-weighting. We first derive the asymptotic expansion of high dimensional kernels under covariate shifts. By a bias-variance decomposition, we theoretically demonstrate that the re-weighting strategy allows for decreasing the variance. For bias, we analyze the regularization of the arbitrary or well-chosen scale, showing that the bias can behave very differently under different regularization scales. In our analysis, the bias and variance can be characterized by the spectral decay of a data-dependent regularized kernel: the original kernel matrix associated with an additional re-weighting matrix, and thus the re-weighting strategy can be regarded as a data-dependent regularization for better understanding. Besides, our analysis provides asymptotic expansion of kernel functions/vectors under covariate shift, which has its own interest.

Revisiting character-level adversarial attacks

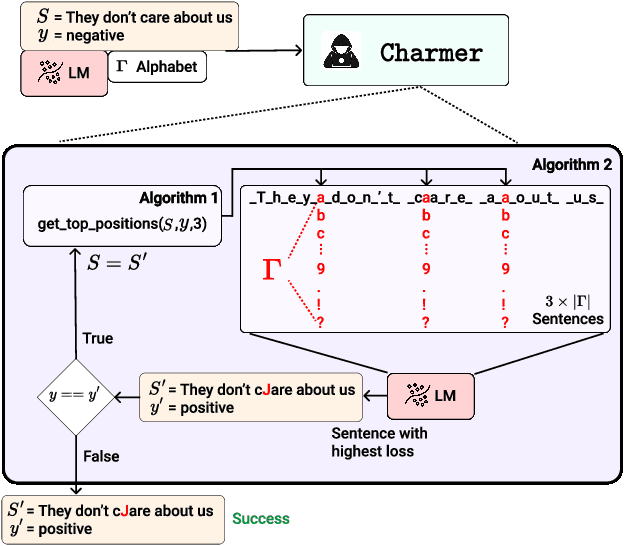
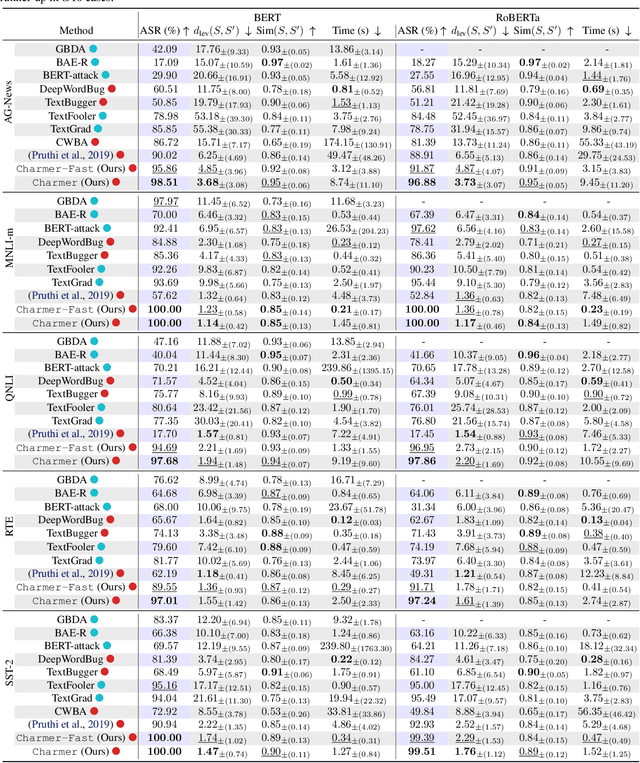
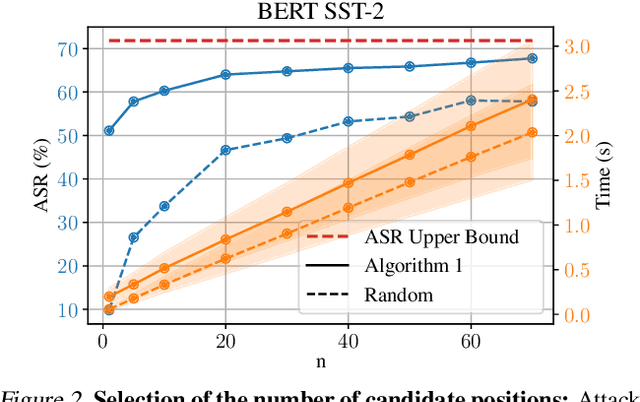
Adversarial attacks in Natural Language Processing apply perturbations in the character or token levels. Token-level attacks, gaining prominence for their use of gradient-based methods, are susceptible to altering sentence semantics, leading to invalid adversarial examples. While character-level attacks easily maintain semantics, they have received less attention as they cannot easily adopt popular gradient-based methods, and are thought to be easy to defend. Challenging these beliefs, we introduce Charmer, an efficient query-based adversarial attack capable of achieving high attack success rate (ASR) while generating highly similar adversarial examples. Our method successfully targets both small (BERT) and large (Llama 2) models. Specifically, on BERT with SST-2, Charmer improves the ASR in 4.84% points and the USE similarity in 8% points with respect to the previous art. Our implementation is available in https://github.com/LIONS-EPFL/Charmer.

Learning with Norm Constrained, Over-parameterized, Two-layer Neural Networks

Recent studies show that a reproducing kernel Hilbert space (RKHS) is not a suitable space to model functions by neural networks as the curse of dimensionality (CoD) cannot be evaded when trying to approximate even a single ReLU neuron (Bach, 2017). In this paper, we study a suitable function space for over-parameterized two-layer neural networks with bounded norms (e.g., the path norm, the Barron norm) in the perspective of sample complexity and generalization properties. First, we show that the path norm (as well as the Barron norm) is able to obtain width-independence sample complexity bounds, which allows for uniform convergence guarantees. Based on this result, we derive the improved result of metric entropy for $\epsilon$-covering up to $\mathcal{O}(\epsilon^{-\frac{2d}{d+2}})$ ($d$ is the input dimension and the depending constant is at most polynomial order of $d$) via the convex hull technique, which demonstrates the separation with kernel methods with $\Omega(\epsilon^{-d})$ to learn the target function in a Barron space. Second, this metric entropy result allows for building a sharper generalization bound under a general moment hypothesis setting, achieving the rate at $\mathcal{O}(n^{-\frac{d+2}{2d+2}})$. Our analysis is novel in that it offers a sharper and refined estimation for metric entropy (with a clear dependence relationship on the dimension $d$) and unbounded sampling in the estimation of the sample error and the output error.

Robust NAS under adversarial training: benchmark, theory, and beyond

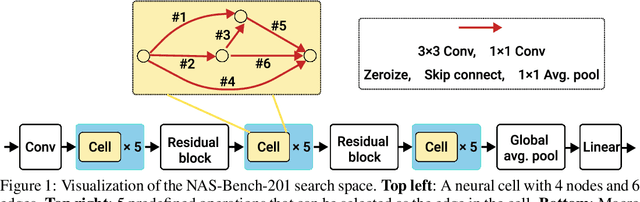
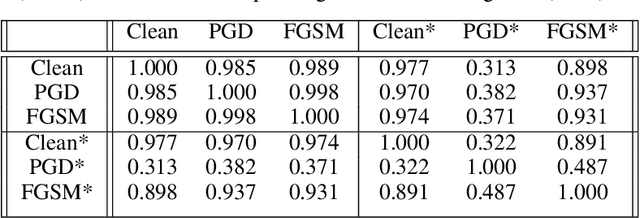
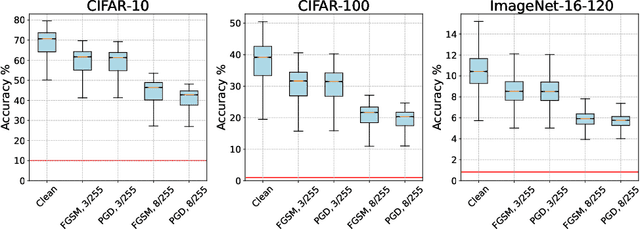
Recent developments in neural architecture search (NAS) emphasize the significance of considering robust architectures against malicious data. However, there is a notable absence of benchmark evaluations and theoretical guarantees for searching these robust architectures, especially when adversarial training is considered. In this work, we aim to address these two challenges, making twofold contributions. First, we release a comprehensive data set that encompasses both clean accuracy and robust accuracy for a vast array of adversarially trained networks from the NAS-Bench-201 search space on image datasets. Then, leveraging the neural tangent kernel (NTK) tool from deep learning theory, we establish a generalization theory for searching architecture in terms of clean accuracy and robust accuracy under multi-objective adversarial training. We firmly believe that our benchmark and theoretical insights will significantly benefit the NAS community through reliable reproducibility, efficient assessment, and theoretical foundation, particularly in the pursuit of robust architectures.

Generalization of Scaled Deep ResNets in the Mean-Field Regime

Despite the widespread empirical success of ResNet, the generalization properties of deep ResNet are rarely explored beyond the lazy training regime. In this work, we investigate \emph{scaled} ResNet in the limit of infinitely deep and wide neural networks, of which the gradient flow is described by a partial differential equation in the large-neural network limit, i.e., the \emph{mean-field} regime. To derive the generalization bounds under this setting, our analysis necessitates a shift from the conventional time-invariant Gram matrix employed in the lazy training regime to a time-variant, distribution-dependent version. To this end, we provide a global lower bound on the minimum eigenvalue of the Gram matrix under the mean-field regime. Besides, for the traceability of the dynamic of Kullback-Leibler (KL) divergence, we establish the linear convergence of the empirical error and estimate the upper bound of the KL divergence over parameters distribution. Finally, we build the uniform convergence for generalization bound via Rademacher complexity. Our results offer new insights into the generalization ability of deep ResNet beyond the lazy training regime and contribute to advancing the understanding of the fundamental properties of deep neural networks.

Can overfitted deep neural networks in adversarial training generalize? -- An approximation viewpoint

Adversarial training is a widely used method to improve the robustness of deep neural networks (DNNs) over adversarial perturbations. However, it is empirically observed that adversarial training on over-parameterized networks often suffers from the \textit{robust overfitting}: it can achieve almost zero adversarial training error while the robust generalization performance is not promising. In this paper, we provide a theoretical understanding of the question of whether overfitted DNNs in adversarial training can generalize from an approximation viewpoint. Specifically, our main results are summarized into three folds: i) For classification, we prove by construction the existence of infinitely many adversarial training classifiers on over-parameterized DNNs that obtain arbitrarily small adversarial training error (overfitting), whereas achieving good robust generalization error under certain conditions concerning the data quality, well separated, and perturbation level. ii) Linear over-parameterization (meaning that the number of parameters is only slightly larger than the sample size) is enough to ensure such existence if the target function is smooth enough. iii) For regression, our results demonstrate that there also exist infinitely many overfitted DNNs with linear over-parameterization in adversarial training that can achieve almost optimal rates of convergence for the standard generalization error. Overall, our analysis points out that robust overfitting can be avoided but the required model capacity will depend on the smoothness of the target function, while a robust generalization gap is inevitable. We hope our analysis will give a better understanding of the mathematical foundations of robustness in DNNs from an approximation view.