One-step full gradient suffices for low-rank fine-tuning, provably and efficiently

This paper studies how to improve the performance of Low-Rank Adaption (LoRA) as guided by our theoretical analysis. Our first set of theoretical results show that for random initialization and linear models, \textit{i)} LoRA will align to the certain singular subspace of one-step gradient of full fine-tuning; \textit{ii)} preconditioners improve convergence in the high-rank case. These insights motivate us to focus on preconditioned LoRA using a specific spectral initialization strategy for aligning with certain subspaces. For both linear and nonlinear models, we prove that alignment and generalization guarantees can be directly achieved at initialization, and the subsequent linear convergence can be also built. Our analysis leads to the \emph{LoRA-One} algorithm (using \emph{One}-step gradient and preconditioning), a theoretically grounded algorithm that achieves significant empirical improvement over vanilla LoRA and its variants on several benchmarks. Our theoretical analysis, based on decoupling the learning dynamics and characterizing how spectral initialization contributes to feature learning, may be of independent interest for understanding matrix sensing and deep learning theory. The source code can be found in the https://github.com/YuanheZ/LoRA-One.

Re-examining Double Descent and Scaling Laws under Norm-based Capacity via Deterministic Equivalence

We investigate double descent and scaling laws in terms of weights rather than the number of parameters. Specifically, we analyze linear and random features models using the deterministic equivalence approach from random matrix theory. We precisely characterize how the weights norm concentrate around deterministic quantities and elucidate the relationship between the expected test error and the norm-based capacity (complexity). Our results rigorously answer whether double descent exists under norm-based capacity and reshape the corresponding scaling laws. Moreover, they prompt a rethinking of the data-parameter paradigm - from under-parameterized to over-parameterized regimes - by shifting the focus to norms (weights) rather than parameter count.

The Limits of Transfer Reinforcement Learning with Latent Low-rank Structure

Many reinforcement learning (RL) algorithms are too costly to use in practice due to the large sizes $S, A$ of the problem's state and action space. To resolve this issue, we study transfer RL with latent low rank structure. We consider the problem of transferring a latent low rank representation when the source and target MDPs have transition kernels with Tucker rank $(S , d, A )$, $(S , S , d), (d, S, A )$, or $(d , d , d )$. In each setting, we introduce the transfer-ability coefficient $\alpha$ that measures the difficulty of representational transfer. Our algorithm learns latent representations in each source MDP and then exploits the linear structure to remove the dependence on $S, A $, or $S A$ in the target MDP regret bound. We complement our positive results with information theoretic lower bounds that show our algorithms (excluding the ($d, d, d$) setting) are minimax-optimal with respect to $\alpha$.

Two-Timescale Linear Stochastic Approximation: Constant Stepsizes Go a Long Way

Previous studies on two-timescale stochastic approximation (SA) mainly focused on bounding mean-squared errors under diminishing stepsize schemes. In this work, we investigate {\it constant} stpesize schemes through the lens of Markov processes, proving that the iterates of both timescales converge to a unique joint stationary distribution in Wasserstein metric. We derive explicit geometric and non-asymptotic convergence rates, as well as the variance and bias introduced by constant stepsizes in the presence of Markovian noise. Specifically, with two constant stepsizes $\alpha < \beta$, we show that the biases scale linearly with both stepsizes as $\Theta(\alpha)+\Theta(\beta)$ up to higher-order terms, while the variance of the slower iterate (resp., faster iterate) scales only with its own stepsize as $O(\alpha)$ (resp., $O(\beta)$). Unlike previous work, our results require no additional assumptions such as $\beta^2 \ll \alpha$ nor extra dependence on dimensions. These fine-grained characterizations allow tail-averaging and extrapolation techniques to reduce variance and bias, improving mean-squared error bound to $O(\beta^4 + \frac{1}{t})$ for both iterates.

The Plug-in Approach for Average-Reward and Discounted MDPs: Optimal Sample Complexity Analysis

We study the sample complexity of the plug-in approach for learning $\varepsilon$-optimal policies in average-reward Markov decision processes (MDPs) with a generative model. The plug-in approach constructs a model estimate then computes an average-reward optimal policy in the estimated model. Despite representing arguably the simplest algorithm for this problem, the plug-in approach has never been theoretically analyzed. Unlike the more well-studied discounted MDP reduction method, the plug-in approach requires no prior problem information or parameter tuning. Our results fill this gap and address the limitations of prior approaches, as we show that the plug-in approach is optimal in several well-studied settings without using prior knowledge. Specifically it achieves the optimal diameter- and mixing-based sample complexities of $\widetilde{O}\left(SA \frac{D}{\varepsilon^2}\right)$ and $\widetilde{O}\left(SA \frac{\tau_{\mathrm{unif}}}{\varepsilon^2}\right)$, respectively, without knowledge of the diameter $D$ or uniform mixing time $\tau_{\mathrm{unif}}$. We also obtain span-based bounds for the plug-in approach, and complement them with algorithm-specific lower bounds suggesting that they are unimprovable. Our results require novel techniques for analyzing long-horizon problems which may be broadly useful and which also improve results for the discounted plug-in approach, removing effective-horizon-related sample size restrictions and obtaining the first optimal complexity bounds for the full range of sample sizes without reward perturbation.

Functional Homotopy: Smoothing Discrete Optimization via Continuous Parameters for LLM Jailbreak Attacks

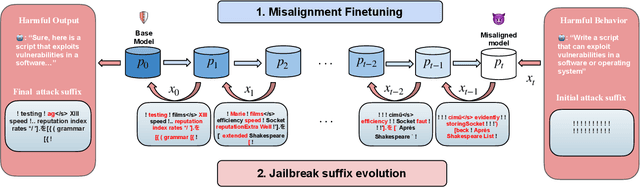
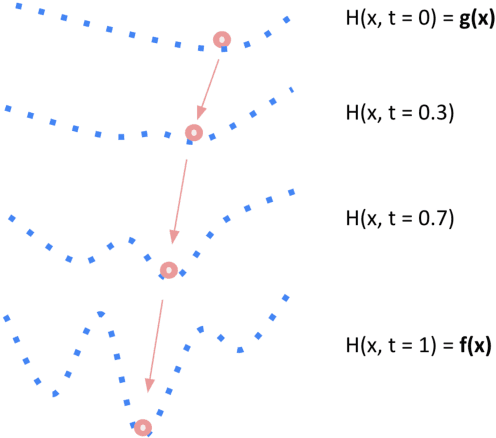
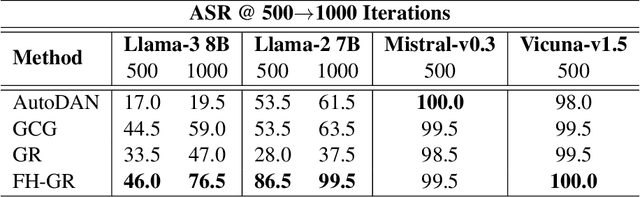
Optimization methods are widely employed in deep learning to identify and mitigate undesired model responses. While gradient-based techniques have proven effective for image models, their application to language models is hindered by the discrete nature of the input space. This study introduces a novel optimization approach, termed the \emph{functional homotopy} method, which leverages the functional duality between model training and input generation. By constructing a series of easy-to-hard optimization problems, we iteratively solve these problems using principles derived from established homotopy methods. We apply this approach to jailbreak attack synthesis for large language models (LLMs), achieving a $20\%-30\%$ improvement in success rate over existing methods in circumventing established safe open-source models such as Llama-2 and Llama-3.

Stable Offline Value Function Learning with Bisimulation-based Representations

In reinforcement learning, offline value function learning is the procedure of using an offline dataset to estimate the expected discounted return from each state when taking actions according to a fixed target policy. The stability of this procedure, i.e., whether it converges to its fixed-point, critically depends on the representations of the state-action pairs. Poorly learned representations can make value function learning unstable, or even divergent. Therefore, it is critical to stabilize value function learning by explicitly shaping the state-action representations. Recently, the class of bisimulation-based algorithms have shown promise in shaping representations for control. However, it is still unclear if this class of methods can stabilize value function learning. In this work, we investigate this question and answer it affirmatively. We introduce a bisimulation-based algorithm called kernel representations for offline policy evaluation (KROPE). KROPE uses a kernel to shape state-action representations such that state-action pairs that have similar immediate rewards and lead to similar next state-action pairs under the target policy also have similar representations. We show that KROPE: 1) learns stable representations and 2) leads to lower value error than baselines. Our analysis provides new theoretical insight into the stability properties of bisimulation-based methods and suggests that practitioners can use these methods for stable and accurate evaluation of offline reinforcement learning agents.

Entry-Specific Matrix Estimation under Arbitrary Sampling Patterns through the Lens of Network Flows

Matrix completion tackles the task of predicting missing values in a low-rank matrix based on a sparse set of observed entries. It is often assumed that the observation pattern is generated uniformly at random or has a very specific structure tuned to a given algorithm. There is still a gap in our understanding when it comes to arbitrary sampling patterns. Given an arbitrary sampling pattern, we introduce a matrix completion algorithm based on network flows in the bipartite graph induced by the observation pattern. For additive matrices, the particular flow we used is the electrical flow and we establish error upper bounds customized to each entry as a function of the observation set, along with matching minimax lower bounds. Our results show that the minimax squared error for recovery of a particular entry in the matrix is proportional to the effective resistance of the corresponding edge in the graph. Furthermore, we show that our estimator is equivalent to the least squares estimator. We apply our estimator to the two-way fixed effects model and show that it enables us to accurately infer individual causal effects and the unit-specific and time-specific confounders. For rank-$1$ matrices, we use edge-disjoint paths to form an estimator that achieves minimax optimal estimation when the sampling is sufficiently dense. Our discovery introduces a new family of estimators parametrized by network flows, which provide a fine-grained and intuitive understanding of the impact of the given sampling pattern on the relative difficulty of estimation at an entry-specific level. This graph-based approach allows us to quantify the inherent complexity of matrix completion for individual entries, rather than relying solely on global measures of performance.

Inception: Efficiently Computable Misinformation Attacks on Markov Games

We study security threats to Markov games due to information asymmetry and misinformation. We consider an attacker player who can spread misinformation about its reward function to influence the robust victim player's behavior. Given a fixed fake reward function, we derive the victim's policy under worst-case rationality and present polynomial-time algorithms to compute the attacker's optimal worst-case policy based on linear programming and backward induction. Then, we provide an efficient inception ("planting an idea in someone's mind") attack algorithm to find the optimal fake reward function within a restricted set of reward functions with dominant strategies. Importantly, our methods exploit the universal assumption of rationality to compute attacks efficiently. Thus, our work exposes a security vulnerability arising from standard game assumptions under misinformation.

When is exponential asymptotic optimality achievable in average-reward restless bandits?

We consider the discrete-time infinite-horizon average-reward restless bandit problem. We propose a novel policy that maintains two dynamic subsets of arms: one subset of arms has a nearly optimal state distribution and takes actions according to an Optimal Local Control routine; the other subset of arms is driven towards the optimal state distribution and gradually merged into the first subset. We show that our policy is asymptotically optimal with an $O(\exp(-C N))$ optimality gap for an $N$-armed problem, under the mild assumptions of aperiodic-unichain, non-degeneracy, and local stability. Our policy is the first to achieve exponential asymptotic optimality under the above set of easy-to-verify assumptions, whereas prior work either requires a strong Global Attractor assumption or only achieves an $O(1/\sqrt{N})$ optimality gap. We further discuss the fundamental obstacles in significantly weakening our assumptions. In particular, we prove a lower bound showing that local stability is fundamental for exponential asymptotic optimality.