Faster Fixed-Point Methods for Multichain MDPs

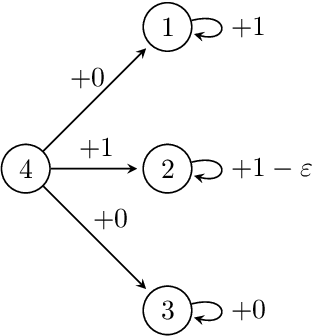
We study value-iteration (VI) algorithms for solving general (a.k.a. multichain) Markov decision processes (MDPs) under the average-reward criterion, a fundamental but theoretically challenging setting. Beyond the difficulties inherent to all average-reward problems posed by the lack of contractivity and non-uniqueness of solutions to the Bellman operator, in the multichain setting an optimal policy must solve the navigation subproblem of steering towards the best connected component, in addition to optimizing long-run performance within each component. We develop algorithms which better solve this navigational subproblem in order to achieve faster convergence for multichain MDPs, obtaining improved rates of convergence and sharper measures of complexity relative to prior work. Many key components of our results are of potential independent interest, including novel connections between average-reward and discounted problems, optimal fixed-point methods for discounted VI which extend to general Banach spaces, new sublinear convergence rates for the discounted value error, and refined suboptimality decompositions for multichain MDPs. Overall our results yield faster convergence rates for discounted and average-reward problems and expand the theoretical foundations of VI approaches.

Optimal Single-Policy Sample Complexity and Transient Coverage for Average-Reward Offline RL

We study offline reinforcement learning in average-reward MDPs, which presents increased challenges from the perspectives of distribution shift and non-uniform coverage, and has been relatively underexamined from a theoretical perspective. While previous work obtains performance guarantees under single-policy data coverage assumptions, such guarantees utilize additional complexity measures which are uniform over all policies, such as the uniform mixing time. We develop sharp guarantees depending only on the target policy, specifically the bias span and a novel policy hitting radius, yielding the first fully single-policy sample complexity bound for average-reward offline RL. We are also the first to handle general weakly communicating MDPs, contrasting restrictive structural assumptions made in prior work. To achieve this, we introduce an algorithm based on pessimistic discounted value iteration enhanced by a novel quantile clipping technique, which enables the use of a sharper empirical-span-based penalty function. Our algorithm also does not require any prior parameter knowledge for its implementation. Remarkably, we show via hard examples that learning under our conditions requires coverage assumptions beyond the stationary distribution of the target policy, distinguishing single-policy complexity measures from previously examined cases. We also develop lower bounds nearly matching our main result.

The Plug-in Approach for Average-Reward and Discounted MDPs: Optimal Sample Complexity Analysis

We study the sample complexity of the plug-in approach for learning $\varepsilon$-optimal policies in average-reward Markov decision processes (MDPs) with a generative model. The plug-in approach constructs a model estimate then computes an average-reward optimal policy in the estimated model. Despite representing arguably the simplest algorithm for this problem, the plug-in approach has never been theoretically analyzed. Unlike the more well-studied discounted MDP reduction method, the plug-in approach requires no prior problem information or parameter tuning. Our results fill this gap and address the limitations of prior approaches, as we show that the plug-in approach is optimal in several well-studied settings without using prior knowledge. Specifically it achieves the optimal diameter- and mixing-based sample complexities of $\widetilde{O}\left(SA \frac{D}{\varepsilon^2}\right)$ and $\widetilde{O}\left(SA \frac{\tau_{\mathrm{unif}}}{\varepsilon^2}\right)$, respectively, without knowledge of the diameter $D$ or uniform mixing time $\tau_{\mathrm{unif}}$. We also obtain span-based bounds for the plug-in approach, and complement them with algorithm-specific lower bounds suggesting that they are unimprovable. Our results require novel techniques for analyzing long-horizon problems which may be broadly useful and which also improve results for the discounted plug-in approach, removing effective-horizon-related sample size restrictions and obtaining the first optimal complexity bounds for the full range of sample sizes without reward perturbation.

Span-Based Optimal Sample Complexity for Weakly Communicating and General Average Reward MDPs

We study the sample complexity of learning an $\epsilon$-optimal policy in an average-reward Markov decision process (MDP) under a generative model. For weakly communicating MDPs, we establish the complexity bound $\tilde{O}(SA\frac{H}{\epsilon^2})$, where $H$ is the span of the bias function of the optimal policy and $SA$ is the cardinality of the state-action space. Our result is the first that is minimax optimal (up to log factors) in all parameters $S,A,H$ and $\epsilon$, improving on existing work that either assumes uniformly bounded mixing times for all policies or has suboptimal dependence on the parameters. We further investigate sample complexity in general (non-weakly-communicating) average-reward MDPs. We argue a new transient time parameter $B$ is necessary, establish an $\tilde{O}(SA\frac{B+H}{\epsilon^2})$ complexity bound, and prove a matching (up to log factors) minimax lower bound. Both results are based on reducing the average-reward MDP to a discounted MDP, which requires new ideas in the general setting. To establish the optimality of this reduction, we develop improved bounds for $\gamma$-discounted MDPs, showing that $\tilde{\Omega}\left(SA\frac{H}{(1-\gamma)^2\epsilon^2}\right)$ samples suffice to learn an $\epsilon$-optimal policy in weakly communicating MDPs under the regime that $\gamma\geq 1-1/H$, and $\tilde{\Omega}\left(SA\frac{B+H}{(1-\gamma)^2\epsilon^2}\right)$ samples suffice in general MDPs when $\gamma\geq 1-\frac{1}{B+H}$. Both these results circumvent the well-known lower bound of $\tilde{\Omega}\left(SA\frac{1}{(1-\gamma)^3\epsilon^2}\right)$ for arbitrary $\gamma$-discounted MDPs. Our analysis develops upper bounds on certain instance-dependent variance parameters in terms of the span and transient time parameters. The weakly communicating bounds are tighter than those based on the mixing time or diameter of the MDP and may be of broader use.

Span-Based Optimal Sample Complexity for Average Reward MDPs

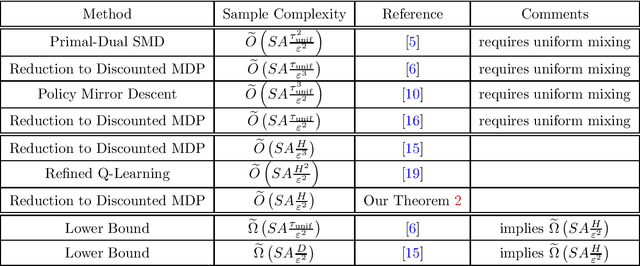
We study the sample complexity of learning an $\varepsilon$-optimal policy in an average-reward Markov decision process (MDP) under a generative model. We establish the complexity bound $\widetilde{O}\left(SA\frac{H}{\varepsilon^2} \right)$, where $H$ is the span of the bias function of the optimal policy and $SA$ is the cardinality of the state-action space. Our result is the first that is minimax optimal (up to log factors) in all parameters $S,A,H$ and $\varepsilon$, improving on existing work that either assumes uniformly bounded mixing times for all policies or has suboptimal dependence on the parameters. Our result is based on reducing the average-reward MDP to a discounted MDP. To establish the optimality of this reduction, we develop improved bounds for $\gamma$-discounted MDPs, showing that $\widetilde{O}\left(SA\frac{H}{(1-\gamma)^2\varepsilon^2} \right)$ samples suffice to learn a $\varepsilon$-optimal policy in weakly communicating MDPs under the regime that $\gamma \geq 1 - \frac{1}{H}$, circumventing the well-known lower bound of $\widetilde{\Omega}\left(SA\frac{1}{(1-\gamma)^3\varepsilon^2} \right)$ for general $\gamma$-discounted MDPs. Our analysis develops upper bounds on certain instance-dependent variance parameters in terms of the span parameter. These bounds are tighter than those based on the mixing time or diameter of the MDP and may be of broader use.

Clustering Without an Eigengap

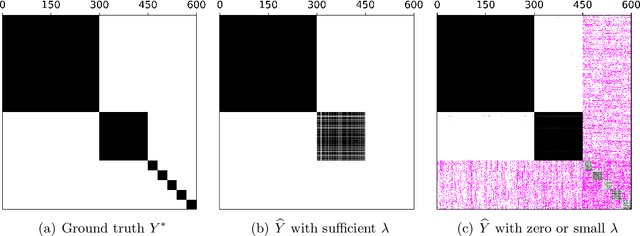
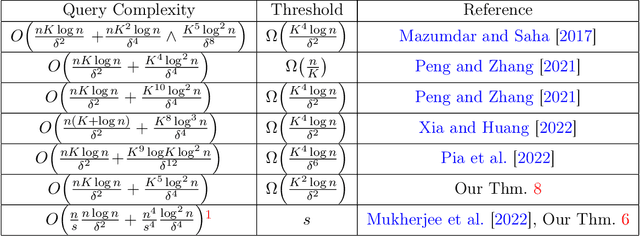
We study graph clustering in the Stochastic Block Model (SBM) in the presence of both large clusters and small, unrecoverable clusters. Previous approaches achieving exact recovery do not allow any small clusters of size $o(\sqrt{n})$, or require a size gap between the smallest recovered cluster and the largest non-recovered cluster. We provide an algorithm based on semidefinite programming (SDP) which removes these requirements and provably recovers large clusters regardless of the remaining cluster sizes. Mid-sized clusters pose unique challenges to the analysis, since their proximity to the recovery threshold makes them highly sensitive to small noise perturbations and precludes a closed-form candidate solution. We develop novel techniques, including a leave-one-out-style argument which controls the correlation between SDP solutions and noise vectors even when the removal of one row of noise can drastically change the SDP solution. We also develop improved eigenvalue perturbation bounds of potential independent interest. Using our gap-free clustering procedure, we obtain efficient algorithms for the problem of clustering with a faulty oracle with superior query complexities, notably achieving $o(n^2)$ sample complexity even in the presence of a large number of small clusters. Our gap-free clustering procedure also leads to improved algorithms for recursive clustering. Our results extend to certain heterogeneous probability settings that are challenging for alternative algorithms.

The Effect of Modeling Human Rationality Level on Learning Rewards from Multiple Feedback Types

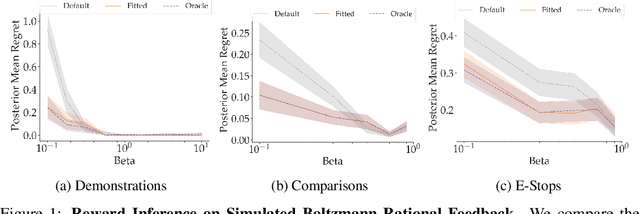
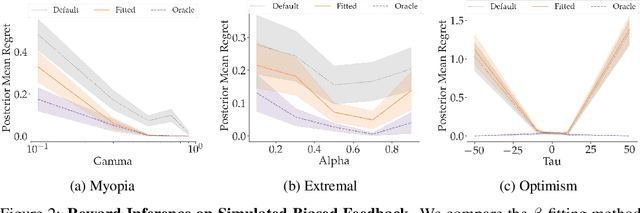
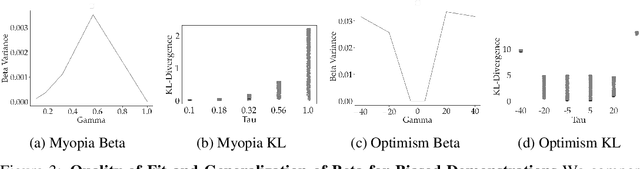
When inferring reward functions from human behavior (be it demonstrations, comparisons, physical corrections, or e-stops), it has proven useful to model the human as making noisy-rational choices, with a "rationality coefficient" capturing how much noise or entropy we expect to see in the human behavior. Many existing works have opted to fix this coefficient regardless of the type, or quality, of human feedback. However, in some settings, giving a demonstration may be much more difficult than answering a comparison query. In this case, we should expect to see more noise or suboptimality in demonstrations than in comparisons, and should interpret the feedback accordingly. In this work, we advocate that grounding the rationality coefficient in real data for each feedback type, rather than assuming a default value, has a significant positive effect on reward learning. We test this in experiments with both simulated feedback, as well a user study. We find that when learning from a single feedback type, overestimating human rationality can have dire effects on reward accuracy and regret. Further, we find that the rationality level affects the informativeness of each feedback type: surprisingly, demonstrations are not always the most informative -- when the human acts very suboptimally, comparisons actually become more informative, even when the rationality level is the same for both. Moreover, when the robot gets to decide which feedback type to ask for, it gets a large advantage from accurately modeling the rationality level of each type. Ultimately, our results emphasize the importance of paying attention to the assumed rationality level, not only when learning from a single feedback type, but especially when agents actively learn from multiple feedback types.

Situational Confidence Assistance for Lifelong Shared Autonomy

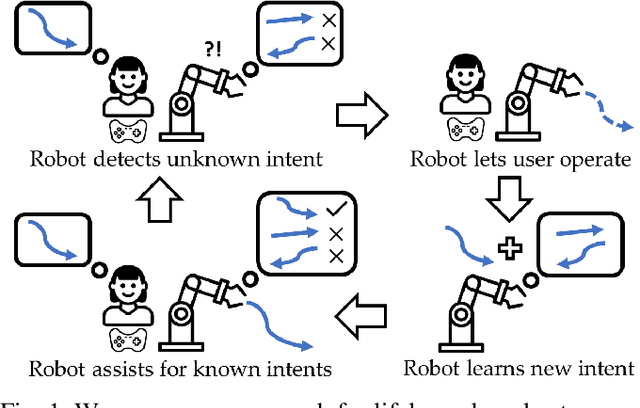
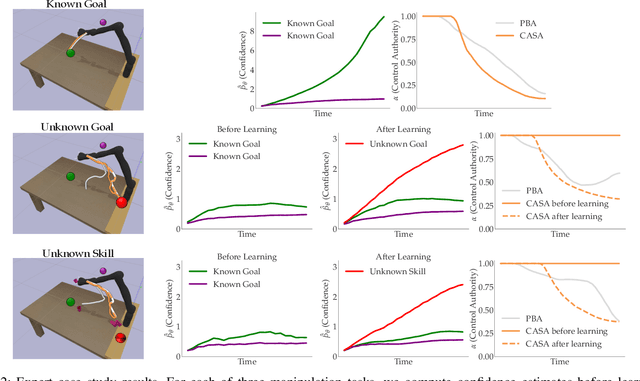
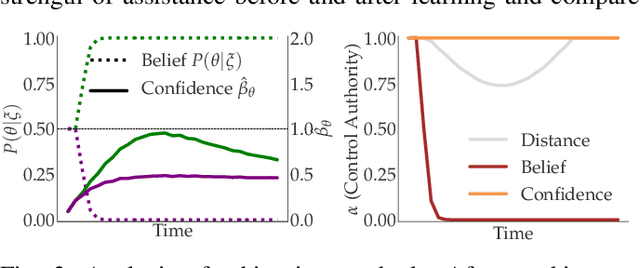
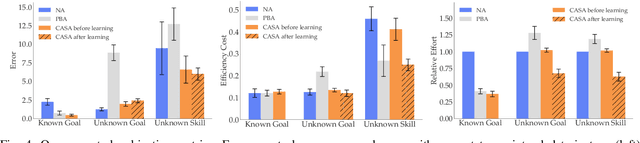
Shared autonomy enables robots to infer user intent and assist in accomplishing it. But when the user wants to do a new task that the robot does not know about, shared autonomy will hinder their performance by attempting to assist them with something that is not their intent. Our key idea is that the robot can detect when its repertoire of intents is insufficient to explain the user's input, and give them back control. This then enables the robot to observe unhindered task execution, learn the new intent behind it, and add it to this repertoire. We demonstrate with both a case study and a user study that our proposed method maintains good performance when the human's intent is in the robot's repertoire, outperforms prior shared autonomy approaches when it isn't, and successfully learns new skills, enabling efficient lifelong learning for confidence-based shared autonomy.