Span-Based Optimal Sample Complexity for Average Reward MDPs
Paper and Code
Nov 22, 2023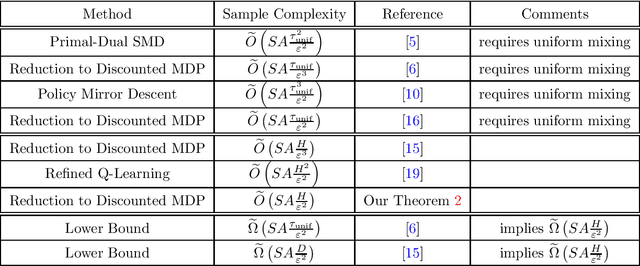
We study the sample complexity of learning an $\varepsilon$-optimal policy in an average-reward Markov decision process (MDP) under a generative model. We establish the complexity bound $\widetilde{O}\left(SA\frac{H}{\varepsilon^2} \right)$, where $H$ is the span of the bias function of the optimal policy and $SA$ is the cardinality of the state-action space. Our result is the first that is minimax optimal (up to log factors) in all parameters $S,A,H$ and $\varepsilon$, improving on existing work that either assumes uniformly bounded mixing times for all policies or has suboptimal dependence on the parameters. Our result is based on reducing the average-reward MDP to a discounted MDP. To establish the optimality of this reduction, we develop improved bounds for $\gamma$-discounted MDPs, showing that $\widetilde{O}\left(SA\frac{H}{(1-\gamma)^2\varepsilon^2} \right)$ samples suffice to learn a $\varepsilon$-optimal policy in weakly communicating MDPs under the regime that $\gamma \geq 1 - \frac{1}{H}$, circumventing the well-known lower bound of $\widetilde{\Omega}\left(SA\frac{1}{(1-\gamma)^3\varepsilon^2} \right)$ for general $\gamma$-discounted MDPs. Our analysis develops upper bounds on certain instance-dependent variance parameters in terms of the span parameter. These bounds are tighter than those based on the mixing time or diameter of the MDP and may be of broader use.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge