Jeremy McMahan
Optimally Installing Strict Equilibria
Mar 05, 2025Abstract:In this work, we develop a reward design framework for installing a desired behavior as a strict equilibrium across standard solution concepts: dominant strategy equilibrium, Nash equilibrium, correlated equilibrium, and coarse correlated equilibrium. We also extend our framework to capture the Markov-perfect equivalents of each solution concept. Central to our framework is a comprehensive mathematical characterization of strictly installable, based on the desired solution concept and the behavior's structure. These characterizations lead to efficient iterative algorithms, which we generalize to handle optimization objectives through linear programming. Finally, we explore how our results generalize to bounded rational agents.
Polynomial-Time Approximability of Constrained Reinforcement Learning
Feb 11, 2025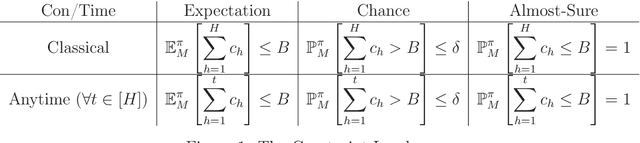
Abstract:We study the computational complexity of approximating general constrained Markov decision processes. Our primary contribution is the design of a polynomial time $(0,\epsilon)$-additive bicriteria approximation algorithm for finding optimal constrained policies across a broad class of recursively computable constraints, including almost-sure, chance, expectation, and their anytime variants. Matching lower bounds imply our approximation guarantees are optimal so long as $P \neq NP$. The generality of our approach results in answers to several long-standing open complexity questions in the constrained reinforcement learning literature. Specifically, we are the first to prove polynomial-time approximability for the following settings: policies under chance constraints, deterministic policies under multiple expectation constraints, policies under non-homogeneous constraints (i.e., constraints of different types), and policies under constraints for continuous-state processes.
Anytime-Constrained Multi-Agent Reinforcement Learning
Oct 31, 2024Abstract:We introduce anytime constraints to the multi-agent setting with the corresponding solution concept being anytime-constrained equilibrium (ACE). Then, we present a comprehensive theory of anytime-constrained Markov games, which includes (1) a computational characterization of feasible policies, (2) a fixed-parameter tractable algorithm for computing ACE, and (3) a polynomial-time algorithm for approximately computing feasible ACE. Since computing a feasible policy is NP-hard even for two-player zero-sum games, our approximation guarantees are the best possible under worst-case analysis. We also develop the first theory of efficient computation for action-constrained Markov games, which may be of independent interest.
Inception: Efficiently Computable Misinformation Attacks on Markov Games
Jun 24, 2024

Abstract:We study security threats to Markov games due to information asymmetry and misinformation. We consider an attacker player who can spread misinformation about its reward function to influence the robust victim player's behavior. Given a fixed fake reward function, we derive the victim's policy under worst-case rationality and present polynomial-time algorithms to compute the attacker's optimal worst-case policy based on linear programming and backward induction. Then, we provide an efficient inception ("planting an idea in someone's mind") attack algorithm to find the optimal fake reward function within a restricted set of reward functions with dominant strategies. Importantly, our methods exploit the universal assumption of rationality to compute attacks efficiently. Thus, our work exposes a security vulnerability arising from standard game assumptions under misinformation.
Roping in Uncertainty: Robustness and Regularization in Markov Games
Jun 13, 2024Abstract:We study robust Markov games (RMG) with $s$-rectangular uncertainty. We show a general equivalence between computing a robust Nash equilibrium (RNE) of a $s$-rectangular RMG and computing a Nash equilibrium (NE) of an appropriately constructed regularized MG. The equivalence result yields a planning algorithm for solving $s$-rectangular RMGs, as well as provable robustness guarantees for policies computed using regularized methods. However, we show that even for just reward-uncertain two-player zero-sum matrix games, computing an RNE is PPAD-hard. Consequently, we derive a special uncertainty structure called efficient player-decomposability and show that RNE for two-player zero-sum RMG in this class can be provably solved in polynomial time. This class includes commonly used uncertainty sets such as $L_1$ and $L_\infty$ ball uncertainty sets.
Deterministic Policies for Constrained Reinforcement Learning in Polynomial-Time
May 23, 2024Abstract:We present a novel algorithm that efficiently computes near-optimal deterministic policies for constrained reinforcement learning (CRL) problems. Our approach combines three key ideas: (1) value-demand augmentation, (2) action-space approximate dynamic programming, and (3) time-space rounding. Under mild reward assumptions, our algorithm constitutes a fully polynomial-time approximation scheme (FPTAS) for a diverse class of cost criteria. This class requires that the cost of a policy can be computed recursively over both time and (state) space, which includes classical expectation, almost sure, and anytime constraints. Our work not only provides provably efficient algorithms to address real-world challenges in decision-making but also offers a unifying theory for the efficient computation of constrained deterministic policies.
Optimal Attack and Defense for Reinforcement Learning
Nov 30, 2023


Abstract:To ensure the usefulness of Reinforcement Learning (RL) in real systems, it is crucial to ensure they are robust to noise and adversarial attacks. In adversarial RL, an external attacker has the power to manipulate the victim agent's interaction with the environment. We study the full class of online manipulation attacks, which include (i) state attacks, (ii) observation attacks (which are a generalization of perceived-state attacks), (iii) action attacks, and (iv) reward attacks. We show the attacker's problem of designing a stealthy attack that maximizes its own expected reward, which often corresponds to minimizing the victim's value, is captured by a Markov Decision Process (MDP) that we call a meta-MDP since it is not the true environment but a higher level environment induced by the attacked interaction. We show that the attacker can derive optimal attacks by planning in polynomial time or learning with polynomial sample complexity using standard RL techniques. We argue that the optimal defense policy for the victim can be computed as the solution to a stochastic Stackelberg game, which can be further simplified into a partially-observable turn-based stochastic game (POTBSG). Neither the attacker nor the victim would benefit from deviating from their respective optimal policies, thus such solutions are truly robust. Although the defense problem is NP-hard, we show that optimal Markovian defenses can be computed (learned) in polynomial time (sample complexity) in many scenarios.
Anytime-Constrained Reinforcement Learning
Nov 14, 2023Abstract:We introduce and study constrained Markov Decision Processes (cMDPs) with anytime constraints. An anytime constraint requires the agent to never violate its budget at any point in time, almost surely. Although Markovian policies are no longer sufficient, we show that there exist optimal deterministic policies augmented with cumulative costs. In fact, we present a fixed-parameter tractable reduction from anytime-constrained cMDPs to unconstrained MDPs. Our reduction yields planning and learning algorithms that are time and sample-efficient for tabular cMDPs so long as the precision of the costs is logarithmic in the size of the cMDP. However, we also show that computing non-trivial approximately optimal policies is NP-hard in general. To circumvent this bottleneck, we design provable approximation algorithms that efficiently compute or learn an arbitrarily accurate approximately feasible policy with optimal value so long as the maximum supported cost is bounded by a polynomial in the cMDP or the absolute budget. Given our hardness results, our approximation guarantees are the best possible under worst-case analysis.
Minimally Modifying a Markov Game to Achieve Any Nash Equilibrium and Value
Nov 02, 2023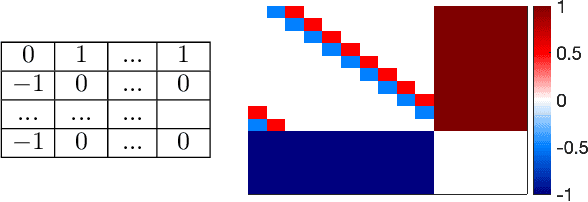
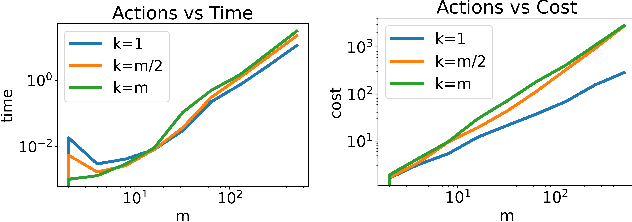
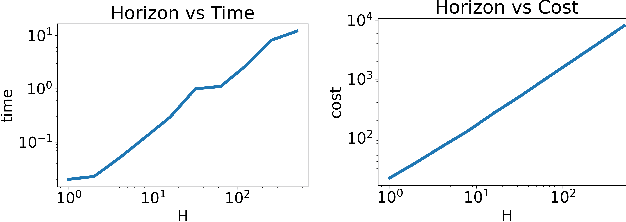
Abstract:We study the game modification problem, where a benevolent game designer or a malevolent adversary modifies the reward function of a zero-sum Markov game so that a target deterministic or stochastic policy profile becomes the unique Markov perfect Nash equilibrium and has a value within a target range, in a way that minimizes the modification cost. We characterize the set of policy profiles that can be installed as the unique equilibrium of some game, and establish sufficient and necessary conditions for successful installation. We propose an efficient algorithm, which solves a convex optimization problem with linear constraints and then performs random perturbation, to obtain a modification plan with a near-optimal cost.
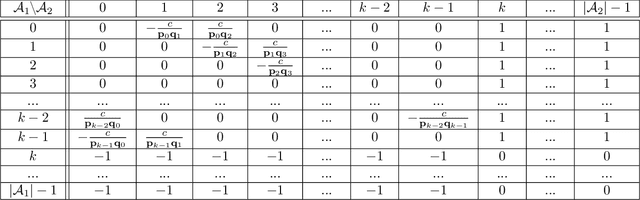
VISER: A Tractable Solution Concept for Games with Information Asymmetry
Jul 18, 2023


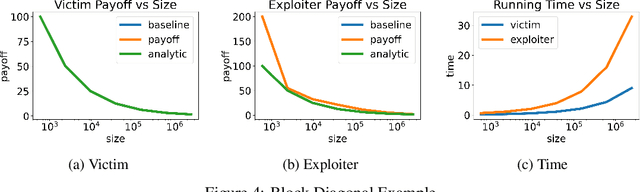
Abstract:Many real-world games suffer from information asymmetry: one player is only aware of their own payoffs while the other player has the full game information. Examples include the critical domain of security games and adversarial multi-agent reinforcement learning. Information asymmetry renders traditional solution concepts such as Strong Stackelberg Equilibrium (SSE) and Robust-Optimization Equilibrium (ROE) inoperative. We propose a novel solution concept called VISER (Victim Is Secure, Exploiter best-Responds). VISER enables an external observer to predict the outcome of such games. In particular, for security applications, VISER allows the victim to better defend itself while characterizing the most damaging attacks available to the attacker. We show that each player's VISER strategy can be computed independently in polynomial time using linear programming (LP). We also extend VISER to its Markov-perfect counterpart for Markov games, which can be solved efficiently using a series of LPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge