A Cramér-von Mises Approach to Incentivizing Truthful Data Sharing

Modern data marketplaces and data sharing consortia increasingly rely on incentive mechanisms to encourage agents to contribute data. However, schemes that reward agents based on the quantity of submitted data are vulnerable to manipulation, as agents may submit fabricated or low-quality data to inflate their rewards. Prior work has proposed comparing each agent's data against others' to promote honesty: when others contribute genuine data, the best way to minimize discrepancy is to do the same. Yet prior implementations of this idea rely on very strong assumptions about the data distribution (e.g. Gaussian), limiting their applicability. In this work, we develop reward mechanisms based on a novel, two-sample test inspired by the Cram\'er-von Mises statistic. Our methods strictly incentivize agents to submit more genuine data, while disincentivizing data fabrication and other types of untruthful reporting. We establish that truthful reporting constitutes a (possibly approximate) Nash equilibrium in both Bayesian and prior-agnostic settings. We theoretically instantiate our method in three canonical data sharing problems and show that it relaxes key assumptions made by prior work. Empirically, we demonstrate that our mechanism incentivizes truthful data sharing via simulations and on real-world language and image data.

Scaling Offline RL via Efficient and Expressive Shortcut Models

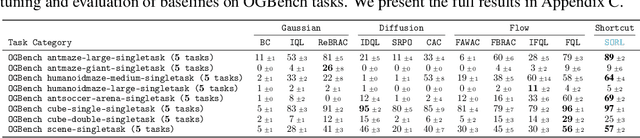
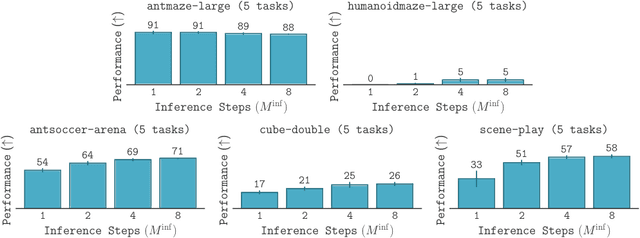
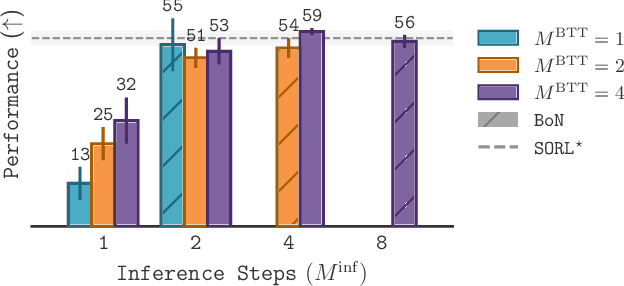
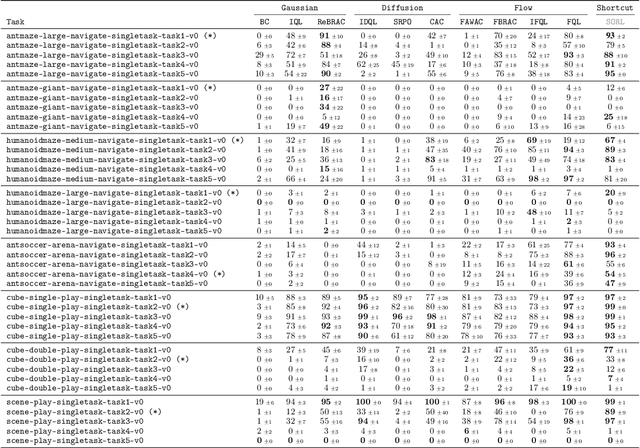
Diffusion and flow models have emerged as powerful generative approaches capable of modeling diverse and multimodal behavior. However, applying these models to offline reinforcement learning (RL) remains challenging due to the iterative nature of their noise sampling processes, making policy optimization difficult. In this paper, we introduce Scalable Offline Reinforcement Learning (SORL), a new offline RL algorithm that leverages shortcut models - a novel class of generative models - to scale both training and inference. SORL's policy can capture complex data distributions and can be trained simply and efficiently in a one-stage training procedure. At test time, SORL introduces both sequential and parallel inference scaling by using the learned Q-function as a verifier. We demonstrate that SORL achieves strong performance across a range of offline RL tasks and exhibits positive scaling behavior with increased test-time compute. We release the code at nico-espinosadice.github.io/projects/sorl.

Efficient Controllable Diffusion via Optimal Classifier Guidance

The controllable generation of diffusion models aims to steer the model to generate samples that optimize some given objective functions. It is desirable for a variety of applications including image generation, molecule generation, and DNA/sequence generation. Reinforcement Learning (RL) based fine-tuning of the base model is a popular approach but it can overfit the reward function while requiring significant resources. We frame controllable generation as a problem of finding a distribution that optimizes a KL-regularized objective function. We present SLCD -- Supervised Learning based Controllable Diffusion, which iteratively generates online data and trains a small classifier to guide the generation of the diffusion model. Similar to the standard classifier-guided diffusion, SLCD's key computation primitive is classification and does not involve any complex concepts from RL or control. Via a reduction to no-regret online learning analysis, we show that under KL divergence, the output from SLCD provably converges to the optimal solution of the KL-regularized objective. Further, we empirically demonstrate that SLCD can generate high quality samples with nearly the same inference time as the base model in both image generation with continuous diffusion and biological sequence generation with discrete diffusion. Our code is available at https://github.com/Owen-Oertell/slcd

Convergence Of Consistency Model With Multistep Sampling Under General Data Assumptions

Diffusion models accomplish remarkable success in data generation tasks across various domains. However, the iterative sampling process is computationally expensive. Consistency models are proposed to learn consistency functions to map from noise to data directly, which allows one-step fast data generation and multistep sampling to improve sample quality. In this paper, we study the convergence of consistency models when the self-consistency property holds approximately under the training distribution. Our analysis requires only mild data assumption and applies to a family of forward processes. When the target data distribution has bounded support or has tails that decay sufficiently fast, we show that the samples generated by the consistency model are close to the target distribution in Wasserstein distance; when the target distribution satisfies some smoothness assumption, we show that with an additional perturbation step for smoothing, the generated samples are close to the target distribution in total variation distance. We provide two case studies with commonly chosen forward processes to demonstrate the benefit of multistep sampling.

Diffusing States and Matching Scores: A New Framework for Imitation Learning

Adversarial Imitation Learning is traditionally framed as a two-player zero-sum game between a learner and an adversarially chosen cost function, and can therefore be thought of as the sequential generalization of a Generative Adversarial Network (GAN). A prominent example of this framework is Generative Adversarial Imitation Learning (GAIL). However, in recent years, diffusion models have emerged as a non-adversarial alternative to GANs that merely require training a score function via regression, yet produce generations of a higher quality. In response, we investigate how to lift insights from diffusion modeling to the sequential setting. We propose diffusing states and performing score-matching along diffused states to measure the discrepancy between the expert's and learner's states. Thus, our approach only requires training score functions to predict noises via standard regression, making it significantly easier and more stable to train than adversarial methods. Theoretically, we prove first- and second-order instance-dependent bounds with linear scaling in the horizon, proving that our approach avoids the compounding errors that stymie offline approaches to imitation learning. Empirically, we show our approach outperforms GAN-style imitation learning baselines across various continuous control problems, including complex tasks like controlling humanoids to walk, sit, and crawl.

Data Sharing for Mean Estimation Among Heterogeneous Strategic Agents

We study a collaborative learning problem where $m$ agents estimate a vector $\mu\in\mathbb{R}^d$ by collecting samples from normal distributions, with each agent $i$ incurring a cost $c_{i,k} \in (0, \infty]$ to sample from the $k^{\text{th}}$ distribution $\mathcal{N}(\mu_k, \sigma^2)$. Instead of working on their own, agents can collect data that is cheap to them, and share it with others in exchange for data that is expensive or even inaccessible to them, thereby simultaneously reducing data collection costs and estimation error. However, when agents have different collection costs, we need to first decide how to fairly divide the work of data collection so as to benefit all agents. Moreover, in naive sharing protocols, strategic agents may under-collect and/or fabricate data, leading to socially undesirable outcomes. Our mechanism addresses these challenges by combining ideas from cooperative and non-cooperative game theory. We use ideas from axiomatic bargaining to divide the cost of data collection. Given such a solution, we develop a Nash incentive-compatible (NIC) mechanism to enforce truthful reporting. We achieve a $\mathcal{O}(\sqrt{m})$ approximation to the minimum social penalty (sum of agent estimation errors and data collection costs) in the worst case, and a $\mathcal{O}(1)$ approximation under favorable conditions. We complement this with a hardness result, showing that $\Omega(\sqrt{m})$ is unavoidable in any NIC mechanism.

Minimally Modifying a Markov Game to Achieve Any Nash Equilibrium and Value

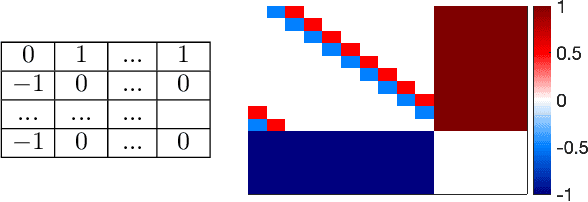
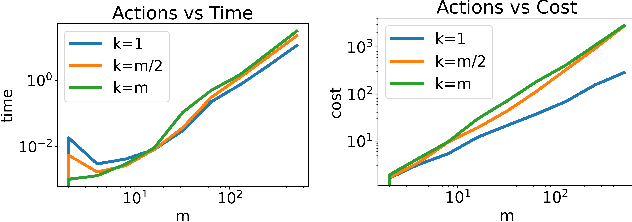
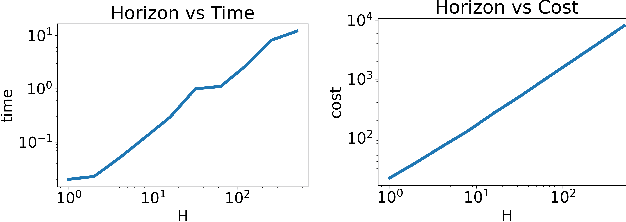
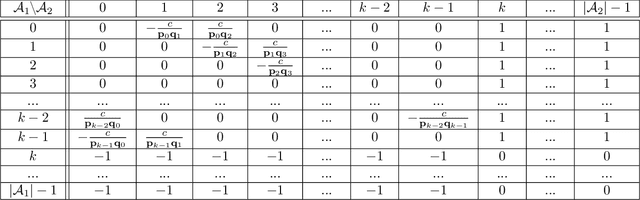
We study the game modification problem, where a benevolent game designer or a malevolent adversary modifies the reward function of a zero-sum Markov game so that a target deterministic or stochastic policy profile becomes the unique Markov perfect Nash equilibrium and has a value within a target range, in a way that minimizes the modification cost. We characterize the set of policy profiles that can be installed as the unique equilibrium of some game, and establish sufficient and necessary conditions for successful installation. We propose an efficient algorithm, which solves a convex optimization problem with linear constraints and then performs random perturbation, to obtain a modification plan with a near-optimal cost.

The Game of Hidden Rules: A New Kind of Benchmark Challenge for Machine Learning

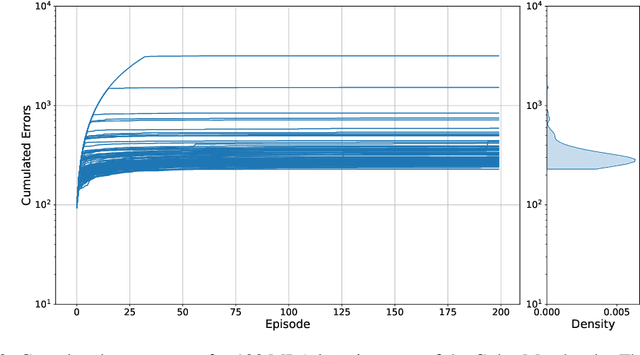
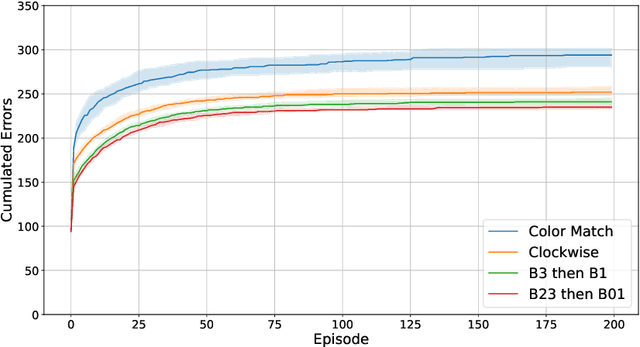
As machine learning (ML) is more tightly woven into society, it is imperative that we better characterize ML's strengths and limitations if we are to employ it responsibly. Existing benchmark environments for ML, such as board and video games, offer well-defined benchmarks for progress, but constituent tasks are often complex, and it is frequently unclear how task characteristics contribute to overall difficulty for the machine learner. Likewise, without a systematic assessment of how task characteristics influence difficulty, it is challenging to draw meaningful connections between performance in different benchmark environments. We introduce a novel benchmark environment that offers an enormous range of ML challenges and enables precise examination of how task elements influence practical difficulty. The tool frames learning tasks as a "board-clearing game," which we call the Game of Hidden Rules (GOHR). The environment comprises an expressive rule language and a captive server environment that can be installed locally. We propose a set of benchmark rule-learning tasks and plan to support a performance leader-board for researchers interested in attempting to learn our rules. GOHR complements existing environments by allowing fine, controlled modifications to tasks, enabling experimenters to better understand how each facet of a given learning task contributes to its practical difficulty for an arbitrary ML algorithm.

Byzantine-Robust Online and Offline Distributed Reinforcement Learning

We consider a distributed reinforcement learning setting where multiple agents separately explore the environment and communicate their experiences through a central server. However, $\alpha$-fraction of agents are adversarial and can report arbitrary fake information. Critically, these adversarial agents can collude and their fake data can be of any sizes. We desire to robustly identify a near-optimal policy for the underlying Markov decision process in the presence of these adversarial agents. Our main technical contribution is Weighted-Clique, a novel algorithm for the robust mean estimation from batches problem, that can handle arbitrary batch sizes. Building upon this new estimator, in the offline setting, we design a Byzantine-robust distributed pessimistic value iteration algorithm; in the online setting, we design a Byzantine-robust distributed optimistic value iteration algorithm. Both algorithms obtain near-optimal sample complexities and achieve superior robustness guarantee than prior works.

Corruption-Robust Offline Reinforcement Learning

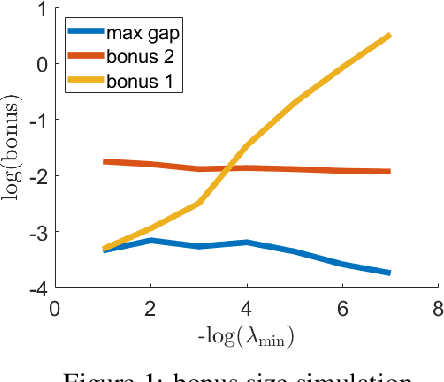
We study the adversarial robustness in offline reinforcement learning. Given a batch dataset consisting of tuples $(s, a, r, s')$, an adversary is allowed to arbitrarily modify $\epsilon$ fraction of the tuples. From the corrupted dataset the learner aims to robustly identify a near-optimal policy. We first show that a worst-case $\Omega(d\epsilon)$ optimality gap is unavoidable in linear MDP of dimension $d$, even if the adversary only corrupts the reward element in a tuple. This contrasts with dimension-free results in robust supervised learning and best-known lower-bound in the online RL setting with corruption. Next, we propose robust variants of the Least-Square Value Iteration (LSVI) algorithm utilizing robust supervised learning oracles, which achieve near-matching performances in cases both with and without full data coverage. The algorithm requires the knowledge of $\epsilon$ to design the pessimism bonus in the no-coverage case. Surprisingly, in this case, the knowledge of $\epsilon$ is necessary, as we show that being adaptive to unknown $\epsilon$ is impossible.This again contrasts with recent results on corruption-robust online RL and implies that robust offline RL is a strictly harder problem.